Kmeans算法、最佳聚类数的确定及散点图-优快云博客

Kmeans算法、最佳聚类数的确定及散点图 ①使用手肘法、轮廓系数法及CH值三种指标来衡量最佳聚类数目 ②使用K-means进行聚类，得出可视化聚类的结果 ③同时得出聚类结果展示（Excel文件） Python代码，备注清晰，替换成自己的数据即可。

最近在做数据聚类分析的项目，用到了Kmeans算法，还研究了如何确定最佳聚类数，最后生成了可视化的散点图，感觉挺有意思的，来和大家分享一下😃

一、最佳聚类数的确定方法

手肘法

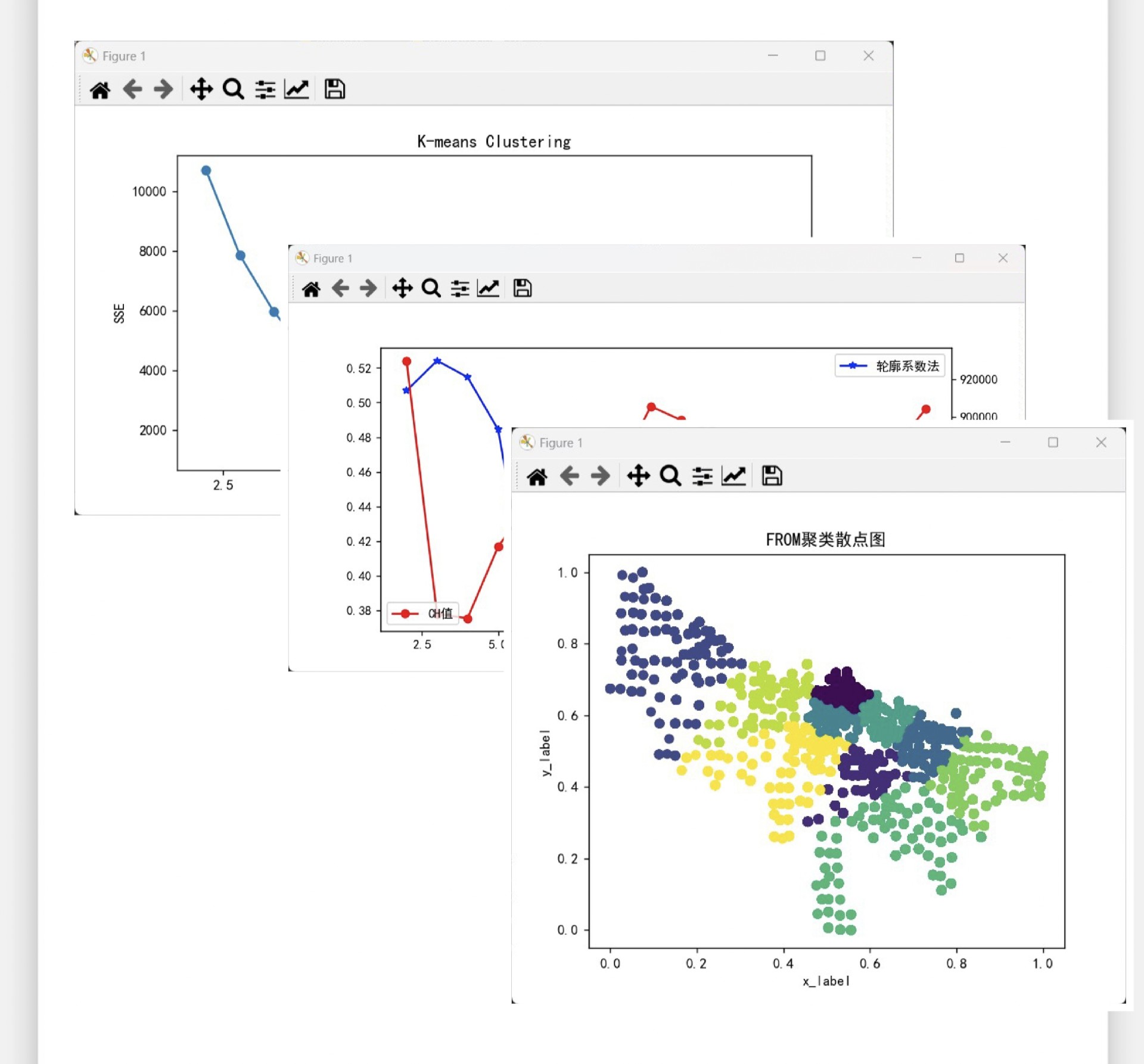
手肘法是一种很直观的确定最佳聚类数的方法。简单来说，就是计算不同聚类数下的聚类误差平方和（SSE），然后绘制SSE随聚类数变化的曲线。当曲线出现明显的拐点时，这个拐点对应的聚类数就是比较合适的最佳聚类数。

用Python实现手肘法的代码如下：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans

# 假设我们有一个数据集data
data = pd.read_csv('your_data.csv')

sse = []
for k in range(1, 11):
    kmeans = KMeans(n_clusters=k, init='k-means++', max_iter=300, n_init=10, random_state=0)
    kmeans.fit(data)
    sse.append(kmeans.inertia_)

plt.plot(range(1, 11), sse)
plt.title('Elbow Method')
plt.xlabel('Number of clusters')
plt.ylabel('SSE')
plt.show()

代码分析：

首先导入需要的库，包括numpy、pandas、matplotlib.pyplot和sklearn.cluster中的KMeans。
读取数据集。这里假设数据集是一个CSV文件，你需要把文件名替换成自己的。
然后通过循环计算不同聚类数（从1到10）下的SSE。每次创建一个KMeans对象，设置好参数后进行拟合，将每次的inertia_（即SSE）添加到sse列表中。
最后绘制SSE随聚类数变化的曲线，通过观察曲线的拐点来初步确定最佳聚类数。

轮廓系数法

轮廓系数法综合考虑了样本点到同簇其他样本的平均距离（a）和到最近簇中样本的平均距离（b）。轮廓系数越接近1，表示聚类效果越好。

from sklearn.metrics import silhouette_score

silhouette_scores = []
for k in range(2, 11):
    kmeans = KMeans(n_clusters=k, init='k-means++', max_iter=300, n_init=10, random_state=0)
    kmeans.fit(data)
    labels = kmeans.labels_
    silhouette_scores.append(silhouette_score(data, labels))

plt.plot(range(2, 11), silhouette_scores)
plt.title('Silhouette Method')
plt.xlabel('Number of clusters')
plt.ylabel('Silhouette Score')
plt.show()

代码分析：

同样先导入必要的库，这里多了sklearn.metrics中的silhouette_score。
循环计算不同聚类数（从2到10）下的轮廓系数。每次拟合模型后获取预测的标签，然后计算轮廓系数并添加到silhouette_scores列表中。
绘制轮廓系数随聚类数变化的曲线，根据曲线峰值来确定最佳聚类数。

CH值

CH值是Calinski-Harabasz Index的缩写，它衡量了聚类的紧密程度和分离程度。CH值越大，聚类效果越好。

from sklearn.metrics import calinski_harabasz_score

ch_scores = []
for k in range(2, 11):
    kmeans = KMeans(n_clusters=k, init='k-means++', max_iter=300, n_init=10, random_state=0)
    kmeans.fit(data)
    labels = kmeans.labels_
    ch_scores.append(calinski_harabasz_score(data, labels))

plt.plot(range(2, 11), ch_scores)
plt.title('Calinski-Harabasz Method')
plt.xlabel('Number of clusters')
plt.ylabel('CH Score')
plt.show()

代码分析：

导入sklearn.metrics中的calinskiharabaszscore。
循环计算不同聚类数（从2到10）下的CH值。过程和前面类似，拟合模型获取标签后计算CH值并添加到ch_scores列表中。
绘制CH值随聚类数变化的曲线，从曲线中找到最佳聚类数。

二、K-means聚类及可视化结果

根据上述方法确定最佳聚类数后，就可以使用K-means进行聚类了。

optimal_k = 3  # 假设最佳聚类数是3，你需要根据前面的分析结果替换
kmeans = KMeans(n_clusters=optimal_k, init='k-means++', max_iter=300, n_init=10, random_state=0)
kmeans.fit(data)
labels = kmeans.labels_

data['Cluster'] = labels

# 保存聚类结果到Excel文件
data.to_excel('cluster_results.xlsx', index=False)

# 绘制散点图
plt.scatter(data.iloc[:, 0], data.iloc[:, 1], c=data['Cluster'])
plt.title('Kmeans Clustering Results')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()

代码分析：