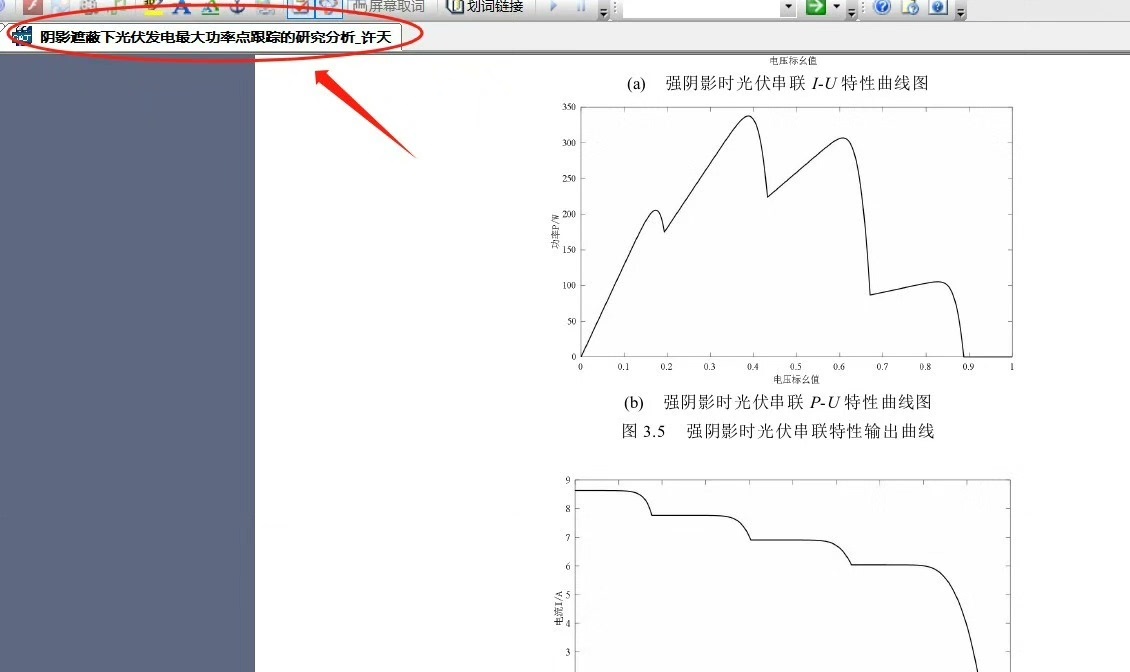
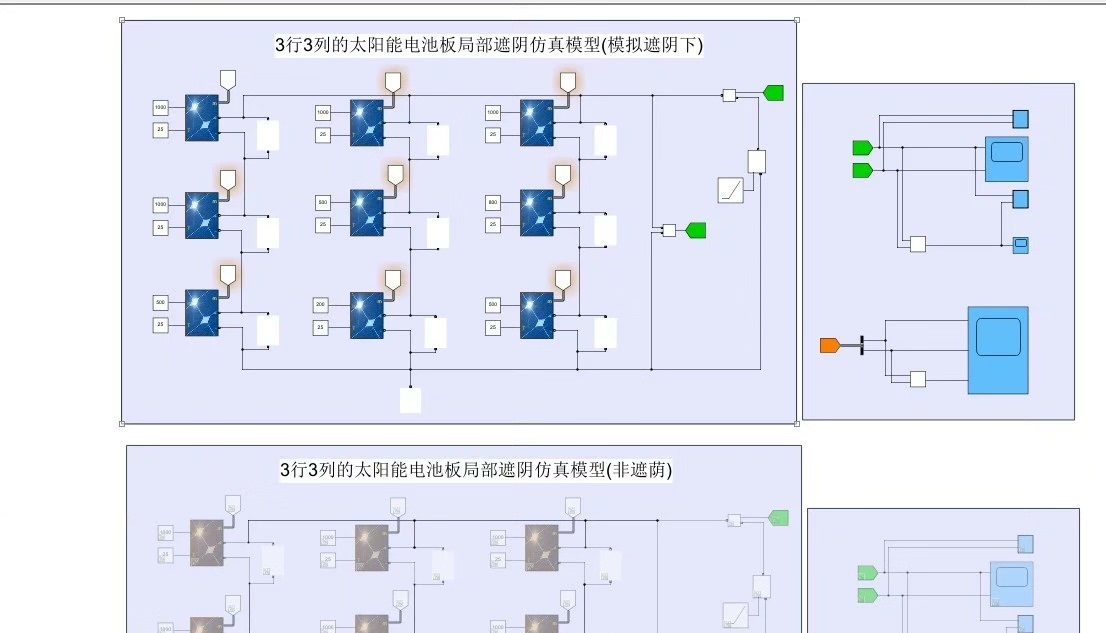
光伏阵列遇到局部阴影就像吃火锅被隔壁桌抢肉——憋屈得很。今天咱们用Python整活，搞个3×3电池板的阴影仿真模型，重点观察串联结构在阴影下的输出曲线怎么抽风-优快云博客

3行3列的太阳能电池板局部遮阴仿真模型可自己更改光照强度，十分方便由于光伏电池的非线性受控电流源的特性，串联光伏阵列和并联光伏阵列在阴影条件下的输出特性是不同的。当串联光伏阵列处于强阴影遮蔽时，即部分光伏电池辐照度严重降低时，光伏输出曲线更容易出现多峰值，当串联光伏阵列处于弱阴影遮蔽时，输出曲线虽无明显的多峰值，其曲线仍会出现极点分别仿真串联模型在阴影时与无遮阴时的I-U特性曲线和P-U特性曲线。

先上核心代码，整个电池模型用单二极管方程硬刚：

def pv_cell(Iph, Is, Rs, Rsh, n, Vt, V):
    # 牛顿迭代法解电流方程
    I = Iph  # 初始值
    for _ in range(20):
        diode = Is * (np.exp((V + I*Rs)/(n*Vt)) - 1)
        I_new = Iph - diode - (V + I*Rs)/Rsh
        if abs(I_new - I) < 1e-6:
            break
        I = I_new
    return min(I, Iph)  # 电流不可能超过光生电流

这个函数相当于每个电池单元的黑匣子，Iph是光生电流（和光照强度正相关），Rs是串联电阻。注意那个min函数可不是摆设，实际电池反向电流受物理限制。

接下来给九宫格电池排兵布阵：

class PVArray:
    def __init__(self, irradiance):
        self.cells = [PVCell(irradiance[i]) for i in range(9)]  # 9个独立单元
    
    def series_output(self, V_total):
        # 串联时总电压分配到各单元，电流取最小值
        I_list = []
        for cell in self.cells:
            V_cell = V_total / 9  # 平均分压
            I = cell.calculate_current(V_cell)
            I_list.append(I)
        return min(I_list)  # 木桶效应

重点在串联时的电流取最小值这个操作，好比水管最细处决定流量。当某个电池被阴影暴击，它的Iph暴跌，直接成为整个链条的瓶颈。

咱们先看全光照（1000W/m²）的情况：

# 正常工况
full_sun = [1000]*9
normal_array = PVArray(full_sun)
voltage = np.linspace(0, 45, 200)
current = [normal_array.series_output(v) for v in voltage]
power = [v*i for v,i in zip(voltage, current)]

输出曲线像座标准小山包（图1），最大功率点约在32V附近。这时候系统就像个听话的乖宝宝，MPPT算法能轻松找到最佳工作点。

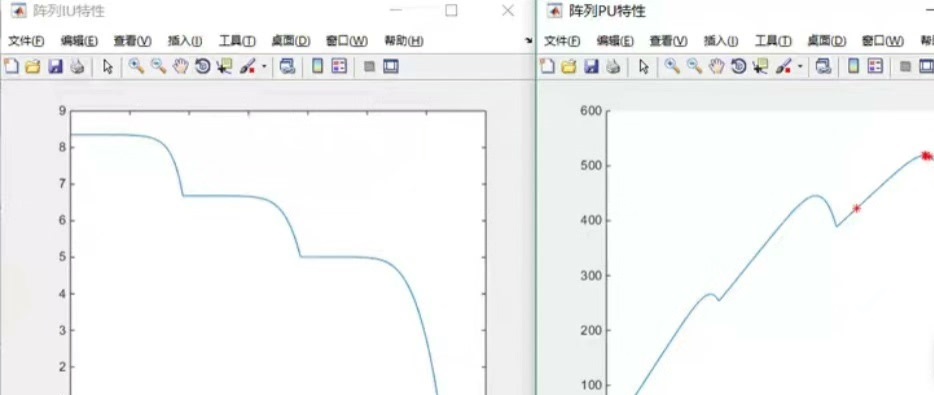
重点戏来了，局部遮阴整起！搞个强阴影场景：中间三个单元辐照度掉到200W/m²

# 中心强阴影
shade_pattern = [1000,1000,1000,
                 1000,200,1000,
                 1000,1000,1000]
shaded_array = PVArray(shade_pattern)

这时候的I-U曲线开始表演杂技（图2），出现明显的双峰现象。第一个峰值在12V附近，对应被阴影电池的极限输出；第二个在28V左右，是正常电池的残余输出。这时候传统MPPT算法容易卡在低功率的局部最优，就像导航软件把你导进死胡同。

换成弱阴影（中间三个降到800W/m²）：

# 边缘弱阴影
weak_shade = [1000,800,1000,
              800,500,800, 
              1000,800,1000]

曲线虽然没出现明显双峰（图3），但在18-24V区间有个功率平台区。这就像开车遇到缓坡，油门踩到底车速却变化不大，MPPT需要更精细的扫描步长。

最后甩个对比图（图4），三条功率曲线同框竞技。阴影导致的功率塌陷肉眼可见，强阴影时最大功率只剩正常情况的1/3。这也解释了为什么实际光伏系统要加旁路二极管——相当于给每个电池单元准备逃生通道，防止被猪队友拖累得太惨。

代码包里准备了交互滑块，拖动就能实时看不同阴影模式的影响（图5）。调参时发现个反直觉现象：有时候适当增加阴影面积反而能提升总输出功率，因为改变了系统的最佳工作点，这或许能给光伏阵列布局提供新思路？