具有执行器饱和及故障的航天器姿态主动容错控制;容错控制;航天器姿态;执行器故障及饱和
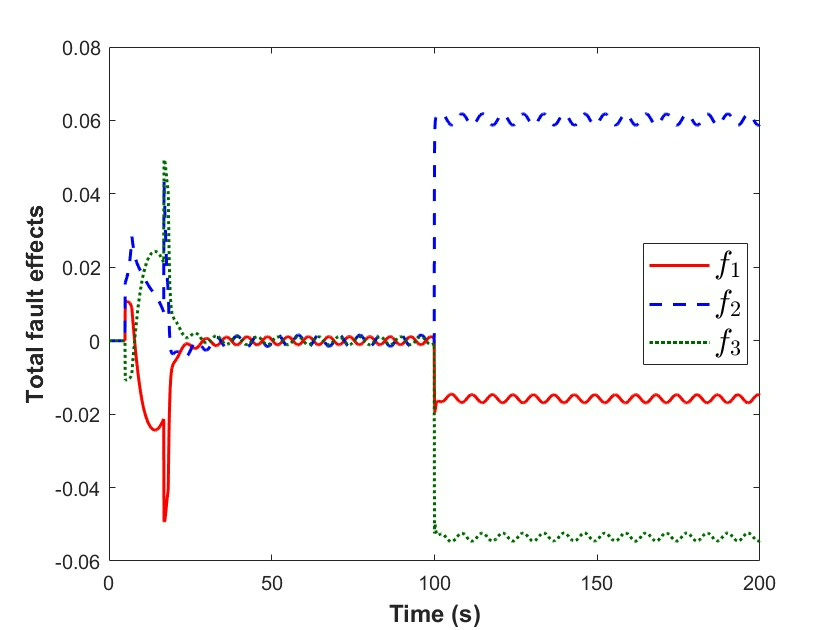
在航天器的复杂运行环境中,姿态控制的稳定性与准确性至关重要。然而,执行器饱和以及故障的出现,常常给姿态控制带来巨大挑战。今天咱们就来唠唠怎么通过主动容错控制策略,让航天器在执行器状况百出的情况下,依旧能稳稳保持姿态。
执行器饱和与故障:航天器姿态控制的拦路虎
执行器饱和,简单来说,就像是人干活儿,力气总有个上限,执行器的输出能力也有极限。当控制指令要求的输出超过这个极限,就会出现饱和现象。比如,航天器姿态调整时,期望某个控制力矩来转动,但执行器能提供的最大力矩却达不到要求,这就影响了姿态调整的精度和速度。
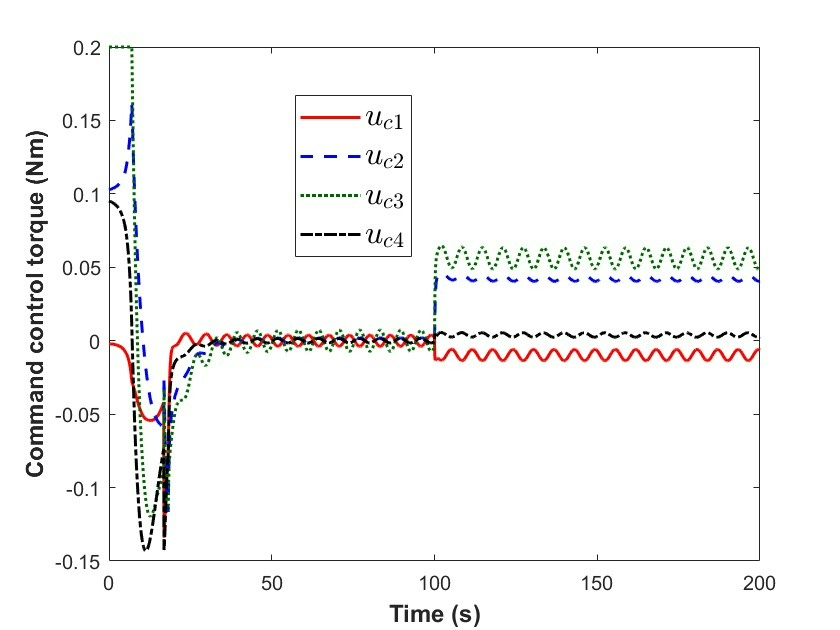
而执行器故障更是麻烦事儿。它可能因为各种原因突然“罢工”,像硬件老化、空间辐射干扰等。一旦执行器故障,航天器就像断了线的风筝,姿态难以有效控制。
容错控制策略:为航天器保驾护航
主动容错控制是解决这些问题的有效手段。它能在执行器出现饱和或故障时,自动调整控制策略,让航天器继续保持稳定姿态。咱们来看段简单代码示例(以Python为例,实际航天器控制可能用更复杂语言和系统):
import numpy as np
# 定义航天器姿态模型参数
I = np.diag([1, 1, 1]) # 惯性矩阵
omega_dot = np.zeros(3) # 初始角速度变化率
omega = np.zeros(3) # 初始角速度
# 模拟执行器输出
def actuator_output(u):
max_output = 10 # 假设执行器最大输出
u_saturated = np.clip(u, -max_output, max_output) # 处理执行器饱和
return u_saturated
# 姿态控制算法
def attitude_control(desired_omega, current_omega, Kp, Ki):
global omega_dot
error = desired_omega - current_omega
integral_error = np.zeros(3)
integral_error += error
u = np.dot(Kp, error) + np.dot(Ki, integral_error)
return actuator_output(u)
# 模拟执行器故障
def actuator_fault(u, fault_index):
fault_magnitude = 0.5 # 假设故障程度
u[fault_index] = u[fault_index] * fault_magnitude # 模拟执行器输出降低
return u代码分析
- 定义航天器姿态模型参数:
I表示航天器的惯性矩阵,它影响着航天器对力矩的响应。omega_dot和omega分别是角速度变化率和角速度的初始值,这俩参数对描述航天器姿态变化很关键。 - 执行器输出函数:
actuator_output函数里,咱们用np.clip来限制执行器输出,模拟执行器饱和情况。这就好比给执行器设定了一个“安全范围”,超出范围就给它拉回来。 - 姿态控制算法:
attitude_control函数实现了基本的控制算法。通过计算期望角速度和当前角速度的误差,再结合比例项Kp和积分项Ki得到控制输入u。这里面比例项能快速响应误差,积分项则能消除稳态误差。最后通过执行器输出函数处理可能的饱和。 - 模拟执行器故障:
actuator_fault函数简单模拟了执行器故障,通过降低指定索引位置的输出值,来模拟执行器部分失效。
在实际航天器姿态控制中,会结合更复杂的动力学模型、故障诊断算法以及自适应控制策略。比如,利用故障诊断算法实时监测执行器状态,一旦检测到故障,马上调整控制算法中的参数,让姿态控制重新回到正轨。
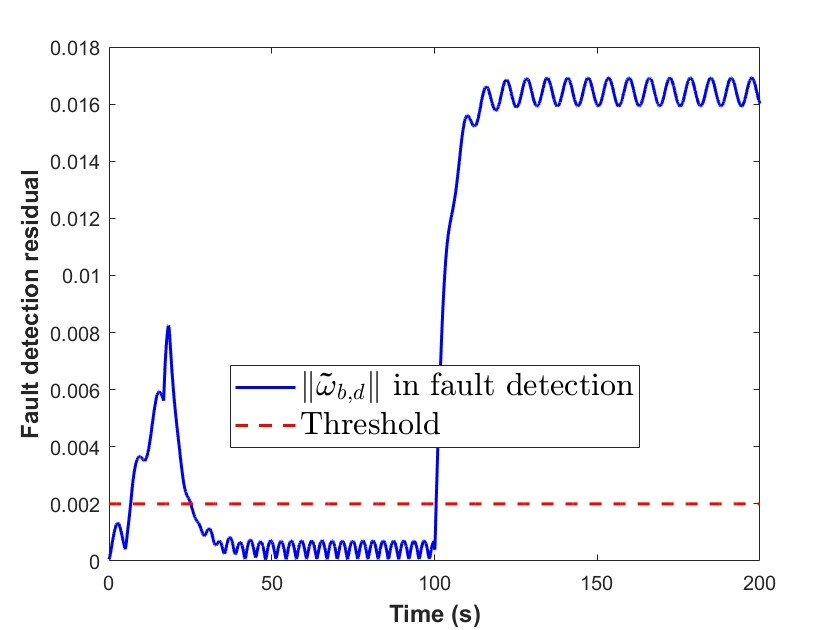
通过这些主动容错控制策略和代码背后的逻辑,我们能让航天器在执行器饱和与故障的恶劣情况下,依旧保持稳定姿态,继续在浩瀚宇宙中顺利执行任务。希望今天的分享能让大家对航天器姿态控制的复杂挑战和解决思路有更深了解。
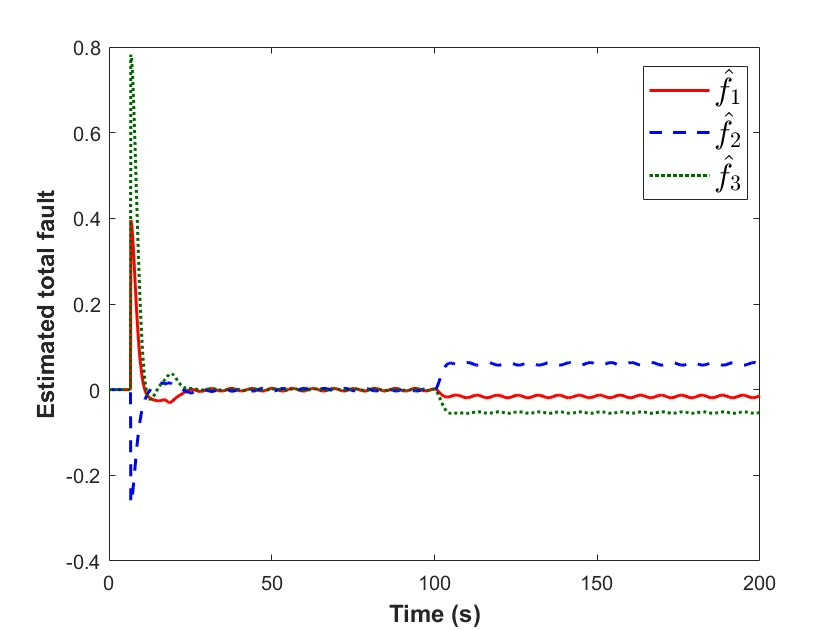
以上代码仅是为辅助理解概念简化编写,实际航天器控制需更严谨和复杂设计。欢迎大家一起探讨更多航天器控制相关有趣话题。




















 995
995

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








