Comsol 多孔介质流固耦合案例：探索孔压与位移的时空演化特征

comsol多孔介质流固耦合案例，孔压、位移时空演化特征。

在工程和科学研究领域，多孔介质的流固耦合问题一直备受关注。比如在石油开采、地下水资源开发以及地质灾害预测等场景中，深入理解多孔介质内流体流动与固体变形之间的相互作用至关重要。而 Comsol 作为一款强大的多物理场仿真软件，为我们研究这类问题提供了便利的工具。今天，就来分享一个基于 Comsol 的多孔介质流固耦合案例，重点探讨孔压与位移的时空演化特征。

案例模型设定

假设我们有一个二维的多孔介质区域，该区域上边界承受一定的荷载，底部固定，两侧为不透水边界。介质本身具有一定的渗透率和弹性模量等特性。为了简化分析，将模型的几何形状设定为矩形，尺寸为 \(Lx \times Ly\)（\(Lx\) 为水平方向长度，\(Ly\) 为垂直方向长度）。

物理场选择与方程

1. 流体流动 - 达西定律：在多孔介质中，流体的流动遵循达西定律，其数学表达式为：
   \(\vec{v} = -\frac{k}{\mu}(\nabla p + \rho g \vec{e}z)\)
   其中，\(\vec{v}\) 是流体的渗流速度矢量，\(k\) 是渗透率，\(\mu\) 是流体动力粘度，\(p\) 是孔隙压力，\(\rho\) 是流体密度，\(g\) 是重力加速度，\(\vec{e}z\) 是垂直方向的单位矢量。在 Comsol 中，我们可以通过选择 “地下水流” 模块来处理这一物理场，软件会自动根据达西定律建立相关方程。
2. 固体力学 - 弹性力学方程：对于固体骨架的变形，我们基于线弹性力学理论。其平衡方程为：
   \(\nabla \cdot \boldsymbol{\sigma} + \vec{f} = 0\)
   其中，\(\boldsymbol{\sigma}\) 是应力张量，\(\vec{f}\) 是体积力。应力应变关系遵循胡克定律，在 Comsol 的 “固体力学” 模块中可以方便地设置这些关系以及材料属性，如弹性模量 \(E\) 和泊松比 \(\nu\) 等。

1. 流固耦合 - 比奥理论：将流体流动与固体变形联系起来的是比奥理论。比奥理论考虑了孔隙压力对固体变形的影响以及固体变形对流体流动的反馈。在 Comsol 中，通过 “多孔弹性” 接口来实现流固耦合的模拟，该接口会自动处理比奥方程中各项的耦合关系。

Comsol 建模步骤与代码实现（部分关键设置）

1. 几何建模：在 Comsol 中创建一个二维矩形几何，使用以下简单的脚本代码（基于 Comsol 的编程语言）来创建矩形：

geom1 = model.geom.create('geom1','Rectangle');
geom1.set('size', [L_x, L_y]);
geom1.set('pos', [0, 0]);

这里 model 是 Comsol 模型对象，geom1 是我们创建的几何实例，通过 set 函数设置矩形的尺寸和位置。

1. 材料属性设置：

mat1 = model.materials.create('mat1');
mat1.select('geom1');
mat1.set('poro', porosity);
mat1.set('perm', k);
mat1.set('E', E_value);
mat1.set('nu', nu_value);

上述代码创建了一个名为 mat1 的材料，选择几何 geom1 应用该材料，并设置了孔隙率 poro、渗透率 perm、弹性模量 E 和泊松比 nu 等材料属性。

1. 边界条件设置：
   - 上边界荷载：

solid1.bnd(1).set('tx', 0);
solid1.bnd(1).set('ty', -load_value);

这里 solid1 是固体力学模块的实例，通过 bnd(1) 选择上边界（假设上边界编号为 1），设置水平方向牵引力 tx 为 0，垂直方向牵引力 ty 为 -load_value（荷载值）。

• 底部固定：

solid1.bnd(2).set('ux', 0);
solid1.bnd(2).set('uy', 0);

选择底部边界（假设编号为 2），限制水平位移 ux 和垂直位移 uy 为 0。

• 两侧不透水边界：

darcy1.bnd([3, 4]).set('bc', 'noFlow');

darcy1 是地下水流模块实例，选择两侧边界（假设编号为 3 和 4），设置边界条件为 “noFlow”，即不透水边界。

1. 网格划分：

mesh1 = model.mesh.create('mesh1');
mesh1.phys('all');
mesh1.elementSize.set('hmax', h_max_value);
mesh1.generate();

创建一个名为 mesh1 的网格对象，应用到所有物理场，设置最大单元尺寸 hmax 为 hmaxvalue，然后生成网格。

1. 求解设置：

study1 = model.studies.create('std1', 'Stationary');
study1.solve();

创建一个名为 std1 的稳态研究，然后进行求解。如果要研究瞬态问题，可以创建瞬态研究并设置时间步长等参数。

孔压与位移的时空演化特征分析

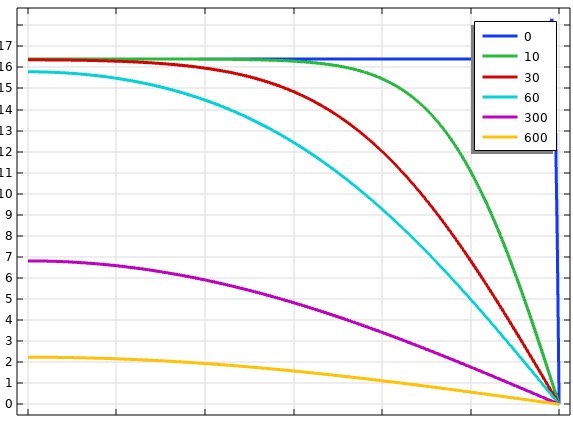
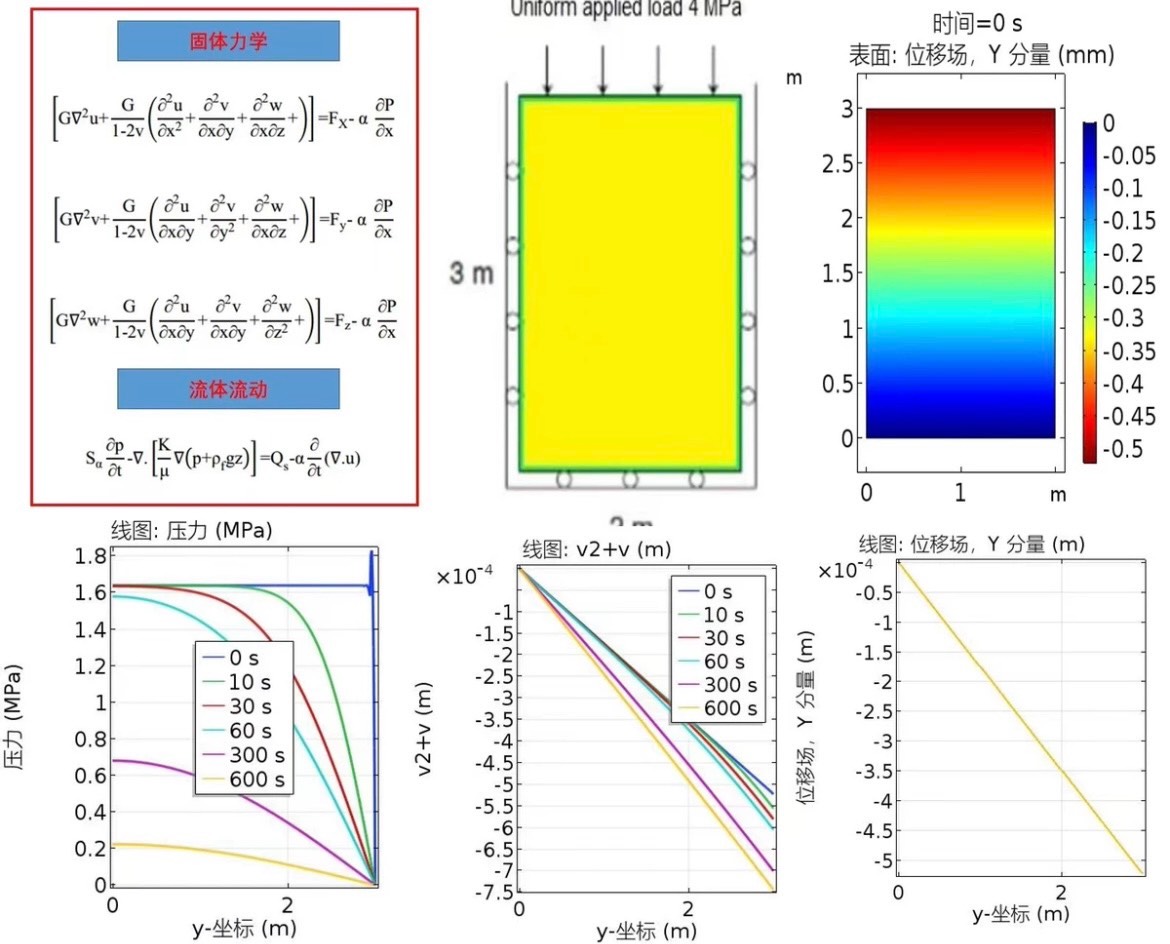
1. 孔压时空演化：通过模拟结果，我们可以绘制不同时刻的孔压云图。在加载初期，上边界附近的孔压迅速升高，因为荷载作用使得流体有向下流动的趋势，但由于底部不透水，流体在短时间内积聚在上部区域。随着时间推移，孔压逐渐向下扩散，形成一个孔压梯度。从数学角度看，这符合达西定律中流体在压力梯度作用下的流动规律。在 Comsol 后处理中，可以通过以下代码提取某一点在不同时刻的孔压值：

point = [x_coord, y_coord];
time_steps = getTimeSteps();
for t = time_steps
    p = model.result.eval('p', 'point', point, 't', t);
    // 这里可以对不同时刻的孔压值 p 进行进一步处理，比如存储到数组中用于绘图等
end

这里 xcoord 和 ycoord 是指定点的坐标，getTimeSteps() 函数获取模拟的时间步，通过 eval 函数在不同时间步下计算该点的孔压 p。

1. 位移时空演化：位移的变化同样有趣。在加载瞬间，固体骨架立即产生弹性变形，上边界处的垂直位移最大，因为此处直接承受荷载。随着时间推移，由于流体流动与固体变形的耦合作用，位移场也会发生变化。例如，当孔压向下扩散时，会导致下部区域的固体骨架受到额外的压力，从而产生进一步的变形。在 Comsol 中，可以通过以下方式绘制位移矢量图来直观展示位移分布：

model.result.create('plot1', 'Streamline');
plot1.set('u', 'ux, uy');
plot1.set('colvar', 'Magnitude(u)');
plot1.show();

上述代码创建了一个流线图 plot1，以显示位移矢量 u（由水平位移 ux 和垂直位移 uy 组成），并以位移矢量的大小作为颜色变量进行可视化。

通过这个 Comsol 多孔介质流固耦合案例，我们深入了解了孔压与位移的时空演化特征。这种模拟分析不仅有助于我们从理论上理解流固耦合现象，也为实际工程问题的解决提供了重要的参考依据。希望大家也能尝试利用 Comsol 进行更多有趣的多物理场模拟研究。