Comsol 中布洛赫表面波场分布图及色散关系探究

原创于 2025-12-01 10:30:00 发布 · 365 阅读

8 ·

CC 4.0 BY-SA版权

文章标签：

#tcpdump

comsol 布洛赫表面波场分布图色散关系能量、传播常数关系

最近在研究光子学相关的内容，其中布洛赫表面波（Bloch Surface Waves, BSWs）引起了我极大的兴趣。今天就来聊聊在 Comsol 中绘制布洛赫表面波场分布图，以及分析其色散关系（能量与传播常数关系）的一些心得。

什么是布洛赫表面波

简单来说，布洛赫表面波是在光子晶体平板等周期性结构表面存在的一种特殊的电磁模式。它具有独特的光学性质，比如可以实现高度局域化的场分布，这在很多光学器件，如传感器、波导等方面有着潜在的应用。

Comsol 建模绘制波场分布图

首先，我们得在 Comsol 里构建合适的模型。以一个简单的一维光子晶体平板模型为例（当然实际应用中可能会涉及更复杂的结构）。

// 定义材料属性
mat1 = materials.air;
mat2 = materials.silicon;

// 创建几何结构
geom1 = model.geom.create('geom1', 2);
geom1.feature.create('block1', 'Block');
geom1.feature.block1.set('size', [1 0.5]);
geom1.feature.create('block2', 'Block');
geom1.feature.block2.set('size', [1 0.5]);
geom1.feature.block2.set('pos', [1 0]);

在这段代码里，我们先定义了两种材料，空气（mat1）和硅（mat2）。然后创建了一个二维几何结构 geom1，并在其中创建了两个块状结构，模拟光子晶体平板的周期性单元。

接下来，就是设置边界条件和求解器。

// 设置边界条件
bc1 = model.physics('emw').bc.create('bc1', 'Electromagnetic Insulation');
bc1.selection.set({'top', 'bottom'});

// 设置求解器
s1 = model.sol.create('s1', 'Eigenfrequency');
s1.study('std1').feature('eig1').set('numeig', 5);

这里我们给模型的上下边界设置了电磁绝缘边界条件 bc1，然后创建了一个本征频率求解器 s1，并且设置求解前 5 个本征模式。

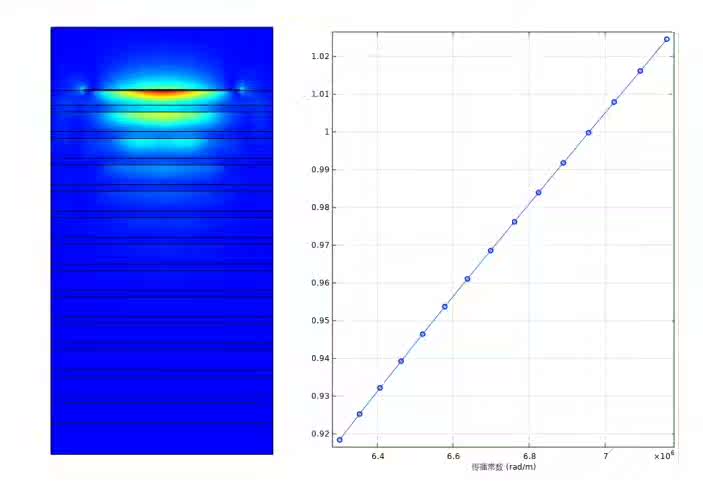
当我们完成这些设置并求解后，就可以绘制布洛赫表面波的场分布图啦。通过后处理功能，选择电场强度等物理量，我们能直观地看到波场在光子晶体平板表面的分布情况。比如，可能会看到场强在平板表面呈现出周期性的增强和减弱，这正是布洛赫表面波局域化特性的一种体现。

色散关系（能量与传播常数关系）分析

色散关系描述了波的能量（频率）与传播常数之间的关系。在 Comsol 里，我们可以通过改变一些参数，比如光子晶体的晶格常数，然后多次求解，得到不同情况下的本征频率和传播常数。

# 假设我们通过脚本获取不同晶格常数下的本征频率和传播常数
lattice_constants = [0.4, 0.5, 0.6]
frequencies = []
propagation_constants = []

for lattice_constant in lattice_constants:
    # 在 Comsol 模型里修改晶格常数
    model.geom.geom1.feature.block1.set('size', [lattice_constant 0.5]);
    model.geom.geom1.feature.block2.set('size', [lattice_constant 0.5]);
    model.geom.geom1.feature.block2.set('pos', [lattice_constant 0]);
    
    # 重新求解
    model.sol.s1.study('std1').run();
    
    # 获取本征频率和传播常数
    freq = model.result('sol1').get('eigval').data('f');
    k = model.result('sol1').get('eigval').data('k');
    
    frequencies.append(freq)
    propagation_constants.append(k)

上面这段 Python 代码模拟了如何通过改变晶格常数，获取对应的本征频率和传播常数。通过这样一系列的数据获取，我们可以绘制出色散曲线。

从色散曲线中，我们能清晰地看到随着传播常数的变化，波的能量（频率）是如何改变的。比如，可能会发现某些频率范围内，传播常数的微小变化会导致频率的急剧变化，这对于理解布洛赫表面波的传播特性和设计基于它的光学器件是非常关键的信息。

总之，通过 Comsol 对布洛赫表面波场分布图的绘制以及色散关系的分析，我们能更深入地理解这种特殊电磁模式的性质，为相关的科研和工程应用打下坚实的基础。希望今天分享的这些内容能给同样对这方面感兴趣的小伙伴一些启发。