四旋翼飞行器(UAV)跟随圆形轨迹模型预测控制(MPC)控制器设计 MPC控制器设计,用于无人机在保持0航向的情况下,以0.1 rad/sec的角速度在5米高度跟踪圆形轨迹。
最近在研究四旋翼飞行器(UAV)的轨迹跟踪问题,特别是如何让无人机在保持0航向的情况下,以0.1 rad/sec的角速度在5米高度跟踪一个圆形轨迹。这个问题听起来简单,但实际操作中涉及到很多控制理论和代码实现。今天就来聊聊如何用模型预测控制(MPC)来实现这个目标。
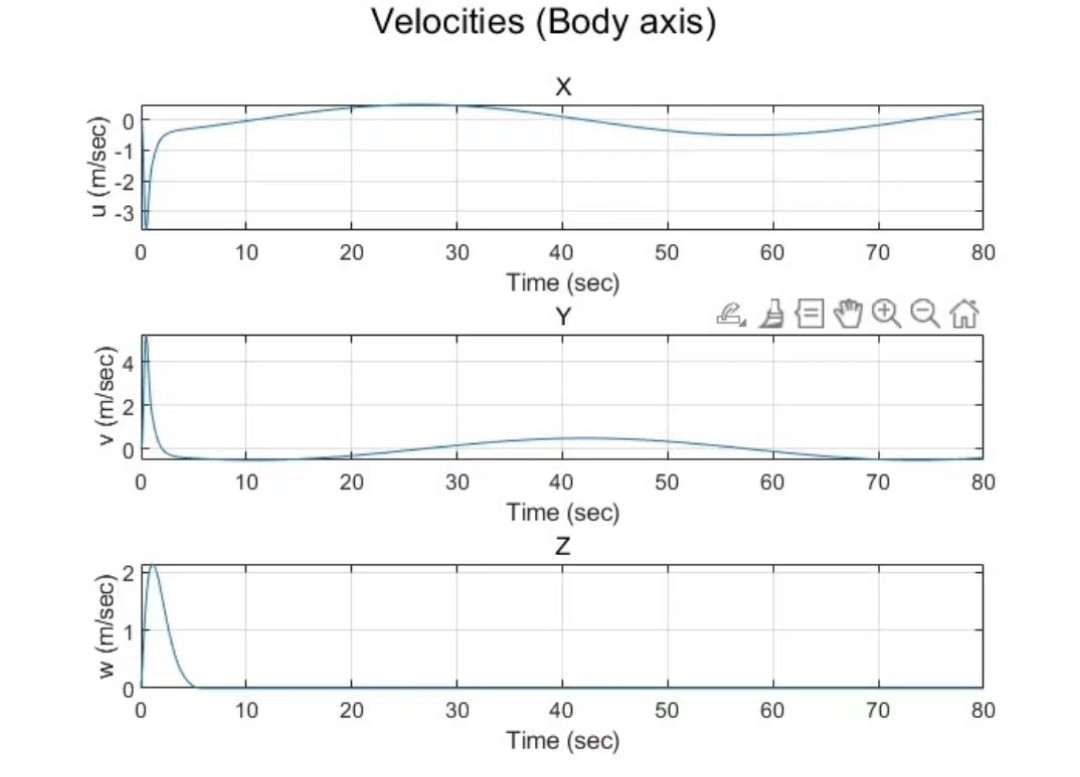
首先,我们需要明确MPC的基本原理。MPC是一种通过预测未来系统的行为来优化当前控制输入的方法。简单来说,就是通过不断预测未来的状态,然后调整当前的控制输入,使得系统能够沿着我们期望的轨迹运动。
对于四旋翼飞行器来说,我们需要建立一个状态空间模型。假设我们忽略一些复杂的动力学因素,可以用以下方程来描述无人机的运动:
import numpy as np
# 控制输入: [roll_cmd, pitch_cmd, thrust_cmd]
def state_space_model(state, control):
x, y, z, vx, vy, vz, roll, pitch, yaw = state
roll_cmd, pitch_cmd, thrust_cmd = control
# 假设重力加速度为9.81 m/s^2
g = 9.81
# 状态更新方程
x_dot = vx
y_dot = vy
z_dot = vz
vx_dot = thrust_cmd * np.sin(pitch_cmd)
vy_dot = -thrust_cmd * np.sin(roll_cmd)
vz_dot = thrust_cmd * np.cos(roll_cmd) * np.cos(pitch_cmd) - g
roll_dot = 0 # 假设保持0航向
pitch_dot = 0 # 假设保持0航向
yaw_dot = 0.1 # 角速度为0.1 rad/sec
return np.array([x_dot, y_dot, z_dot, vx_dot, vy_dot, vz_dot, roll_dot, pitch_dot, yaw_dot])这个模型虽然简化了很多,但足以让我们理解MPC的基本原理。接下来,我们需要设计一个MPC控制器。MPC的核心思想是通过优化问题来求解控制输入。我们可以用以下代码来实现一个简单的MPC控制器:
from scipy.optimize import minimize
def mpc_controller(state, setpoint, horizon=10):
def cost_function(control_sequence):
predicted_state = state
cost = 0
for control in control_sequence:
predicted_state = predicted_state + state_space_model(predicted_state, control) * dt
cost += np.sum((predicted_state - setpoint) ** 2)
return cost
# 初始猜测的控制输入序列
initial_guess = np.zeros((horizon, 3))
# 优化控制输入序列
result = minimize(cost_function, initial_guess, method='BFGS')
return result.x[0] # 返回第一个控制输入在这段代码中,我们定义了一个cost_function,它计算预测状态与设定点之间的误差。然后我们使用scipy.optimize.minimize来最小化这个误差,得到最优的控制输入序列。最后,我们只取第一个控制输入作为当前的控制命令。
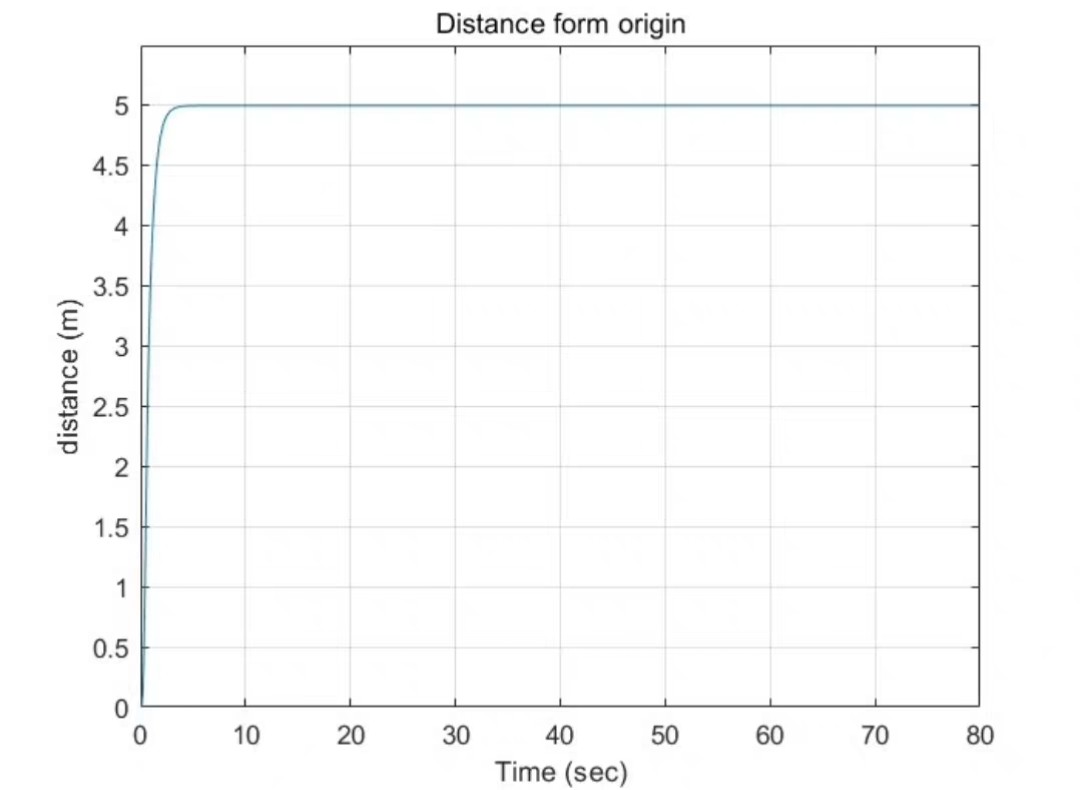
在实际应用中,MPC控制器的性能很大程度上取决于模型的准确性和优化算法的效率。为了进一步提高控制精度,我们可以考虑更复杂的动力学模型,或者使用更高效的优化算法。
最后,来看一下如何在仿真中应用这个MPC控制器:
import matplotlib.pyplot as plt
# 初始状态
state = np.array([0, 0, 5, 0, 0, 0, 0, 0, 0])
setpoint = np.array([5 * np.cos(0.1 * t), 5 * np.sin(0.1 * t), 5, 0, 0, 0, 0, 0, 0])
# 仿真时间步长
dt = 0.1
# 仿真时间
t = np.arange(0, 100, dt)
# 记录轨迹
trajectory = []
for time in t:
control = mpc_controller(state, setpoint)
state = state + state_space_model(state, control) * dt
trajectory.append(state)
# 绘制轨迹
trajectory = np.array(trajectory)
plt.plot(trajectory[:, 0], trajectory[:, 1])
plt.xlabel('X Position')
plt.ylabel('Y Position')
plt.title('UAV Circular Trajectory Tracking')
plt.show()在这个仿真中,我们让无人机从初始状态开始,通过MPC控制器不断调整控制输入,最终跟踪一个圆形轨迹。通过绘制轨迹图,我们可以看到无人机是否能够准确跟踪设定的圆形轨迹。
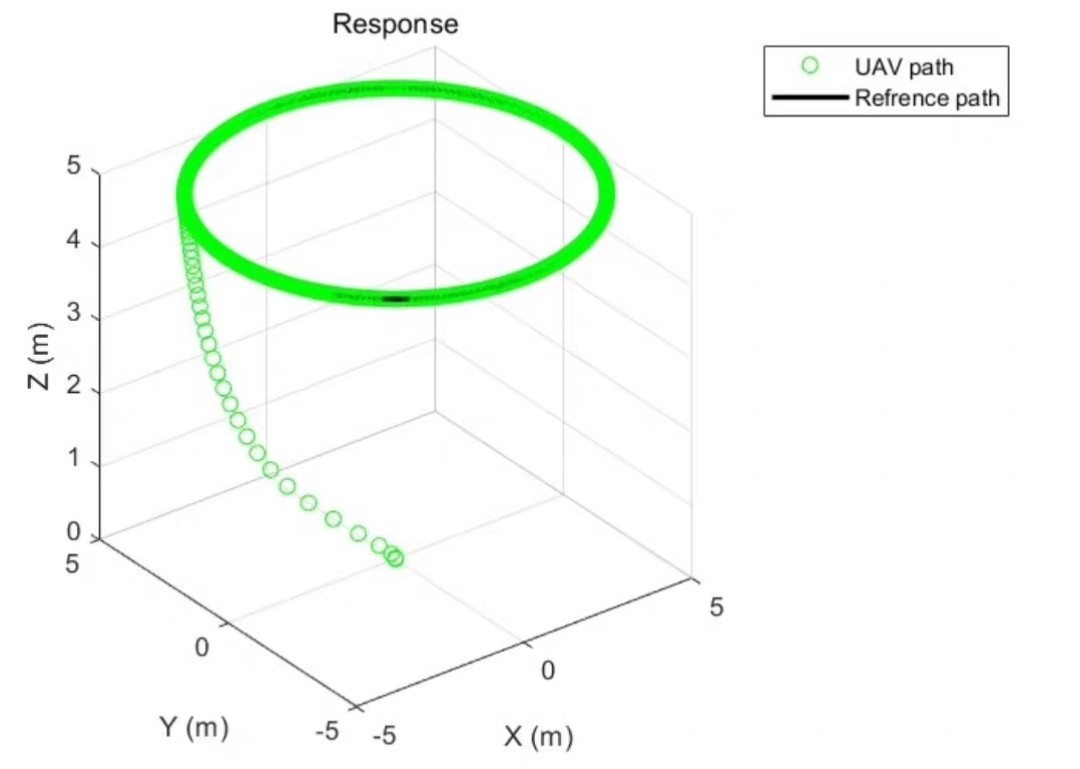
总的来说,MPC控制器在四旋翼飞行器的轨迹跟踪中表现出了良好的性能。虽然这里我们使用了一个简化的模型,但通过不断优化和调整,MPC控制器可以在更复杂的场景中发挥重要作用。希望这篇文章能对你在无人机控制方面的研究有所帮助!




















 126
126

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








