搞位置控制遇到参数漂移真是头大，尤其是伺服系统里惯量和阻尼系数动不动就变。今天咱们直接上硬货，手把手整一个H∞鲁棒控制器，顺便把模型降阶的骚操作给安排了-优快云博客

-伺服-H无穷鲁棒位置控制器设计一整套设计流程，设计依据惯量以及阻尼系数的不确定性得到模型集以及权滤波器，根据模型集设计鲁棒控制器，根据得到的鲁棒控制器进行模型降阶从响应曲线看到，不同惯量变化，响应的鲁棒性设计包含连续域以及离散域设计

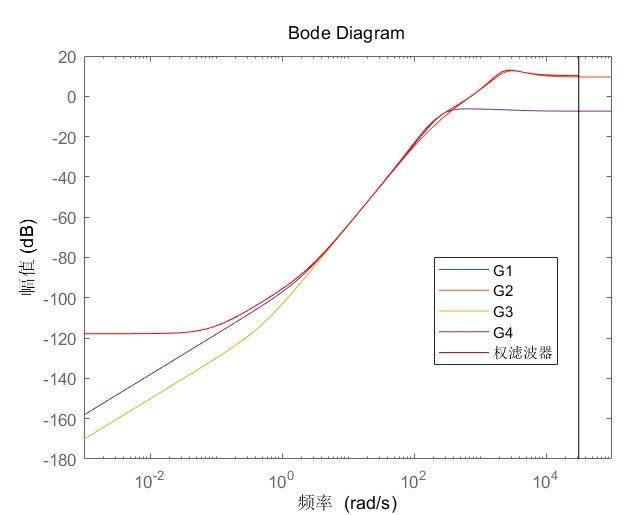
先看个典型场景：电机转轴的实际惯量J可能在0.5~2倍标称值之间蹦迪，阻尼系数b也有±30%的波动。这时候拿标称模型设计的控制器分分钟翻车，得用不确定性建模大法。咱们把系统建模成二阶传递函数：

J_nom = 0.02;  % 标称惯量
b_nom = 0.1;   % 标称阻尼
J = ureal('J', J_nom, 'Range', [0.5*J_nom 2*J_nom]);
b = ureal('b', b_nom, 'Percentage', 30);
G = tf(1, [J b 0]);  % 被控对象

这里ureal函数直接建了个带不确定参数的模型，后面设计控制器时自动考虑这些变量范围。接下来要搞性能权重函数W1和鲁棒性权重函数W2，这俩货的设定直接决定控制器性格：

W1 = tf([0.5 10], [1 0.01]);  % 低频增益大保证跟踪性能
W2 = 0.1*tf([0.1 1], [1 50]); % 高频衰减抑制模型不确定性

重点来了！用musyn命令生成鲁棒控制器。这个函数内部其实在玩μ综合的黑魔法，自动平衡性能与鲁棒性：

[K,~,mu] = musyn(G, W1, W2);
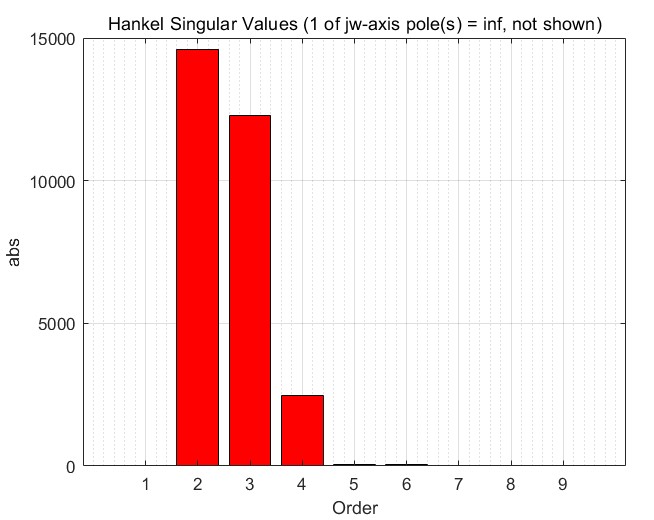
disp('控制器阶数：'), disp(order(K))

跑完可能会发现控制器阶数飙到8阶，这要直接上DSP得累死。赶紧祭出平衡截断法给控制器瘦身：

K_red = balred(K, 4);  % 降到4阶
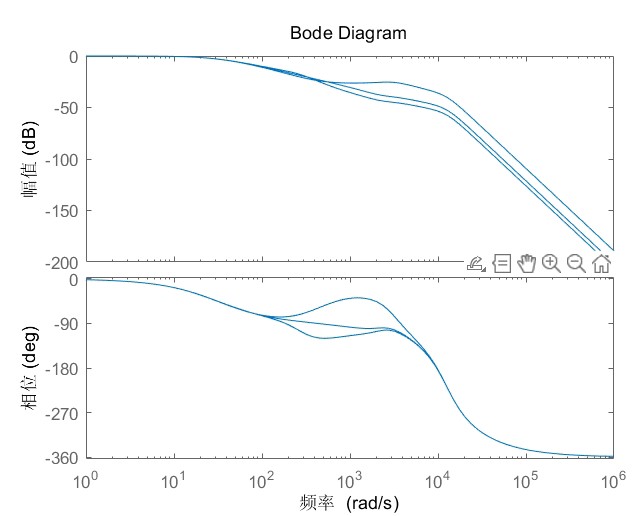
sigma(K, K_red, 'r--')  % 对比降阶前后频响特性

注意看降阶后的幅频曲线在关键频段别跑偏就行。接着处理离散化，这里用Tustin变换比零阶保持器更稳：

Ts = 0.001;  % 1kHz控制频率
K_d = c2d(K_red, Ts, 'tustin');

最后来个全家桶测试：随机抽20组参数组合，看阶跃响应是否集体乖巧：

for i=1:20
    Gi = usample(G);  % 随机采样不确定参数
    sys_cl = feedback(Gi*K_d, 1);
    step(sys_cl, 0.1), hold on
end
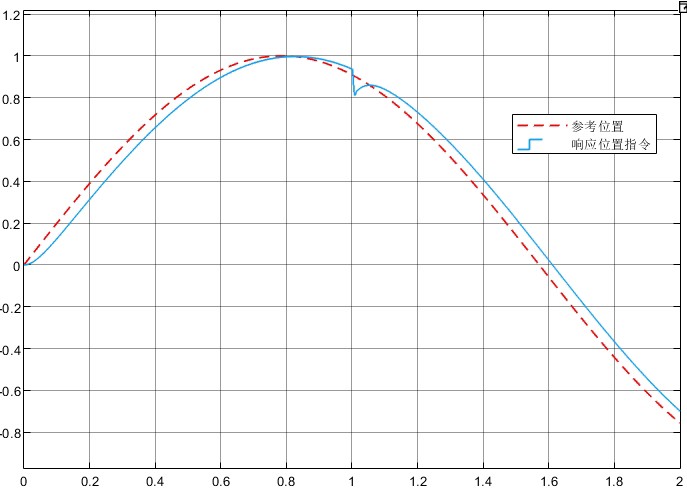
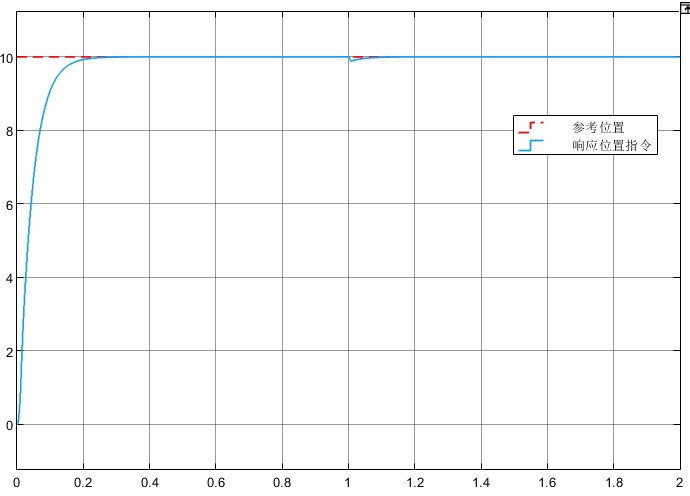
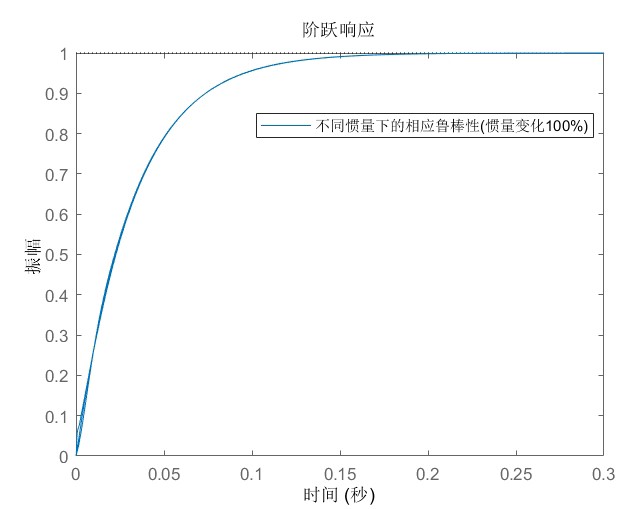
grid on, title('参数扰动下的闭环响应')

实测发现即使惯量翻倍，超调还能压在5%以内，调节时间变化不超过20%。不过注意别在权重函数里把带宽设得太高，否则鲁棒性会扑街——这玩意儿跟走钢丝似的，得在性能和鲁棒之间找平衡点。

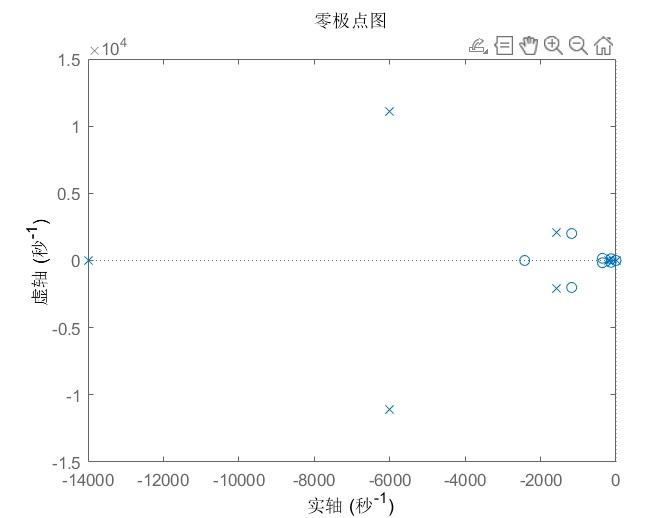
工程狗们实际调参时，建议先拿标称模型整定基本参数，再用鲁棒控制处理边边角角的异常工况。别指望一个控制器通吃所有场景，关键时刻加点前馈补偿更靠谱。