基于Logistic函数的负荷需求响应模型：利用Matlab编程实现电价激励下的负荷转移对比

原创于 2025-11-03 16:45:00 发布 · 587 阅读

8 ·

CC 4.0 BY-SA版权

文章标签：

#transformer

负荷需求响应模型基于Logistic函数采用matlab编程，考虑电价激励下的乐观响应和悲观响应，利用负荷需求响应模型得到峰转平、平转谷的实际负荷转移率，从而得到基于Logistic函数的负荷转移对比，程序运行稳定

引言

在现代电力系统中，负荷侧需求响应（Demand Response, DR）作为提升电网运行效率、促进可再生能源消纳、降低峰谷差的重要手段，正日益受到学术界与工业界的广泛关注。如何构建科学、合理的用户响应模型，准确刻画用户在不同电价激励下的用电行为变化，是需求响应策略成功实施的关键。本文基于上传的MATLAB实现代码，深入剖析一种结合Logistic函数、融合用户乐观与悲观心理预期的负荷侧需求响应建模方法，重点阐述其核心思想、功能流程与关键技术实现。

模型核心思想

该模型的核心在于利用Logistic函数模拟用户在不同电价差激励下的负荷转移意愿，并创新性地引入乐观响应与悲观响应两种边界情景，通过模糊隶属度机制进行动态加权融合，从而得到更贴近实际、更具鲁棒性的综合响应率。模型主要考虑三种典型的负荷转移路径：

峰转平（Peak-to-Flat）：将高峰时段的部分负荷转移至平段。
峰转谷（Peak-to-Valley）：将高峰时段的部分负荷转移至谷段。
谷转平（Valley-to-Flat）：将谷段的部分负荷转移至平段（代码中隐含实现）。

功能流程详解

1. 参数初始化与场景定义

代码首先定义了两组关键参数，分别对应用户的两种心理预期：

乐观参数集：代表用户对电价信号高度敏感，愿意积极响应。
悲观参数集：代表用户对电价变动反应迟钝或存在抵触情绪。

同时，模型设定了分时电价（峰、平、谷）的具体数值，并构建了全天24小时的电价序列 dj 和原始负荷数据 pload1。

2. 基于Logistic函数的边界响应率计算

对于任意两种时段（如峰与谷）之间的价差 Δprice，模型分别计算乐观与悲观情景下的负荷转移率（lammax 和 lammin）。

乐观转移率 (lammax)：使用乐观参数，通过Logistic函数计算得出，代表在该价差下用户可能达到的最大负荷转移比例。
悲观转移率 (lammin)：使用悲观参数，通过同样的Logistic函数计算得出，代表用户可能的最低负荷转移比例。

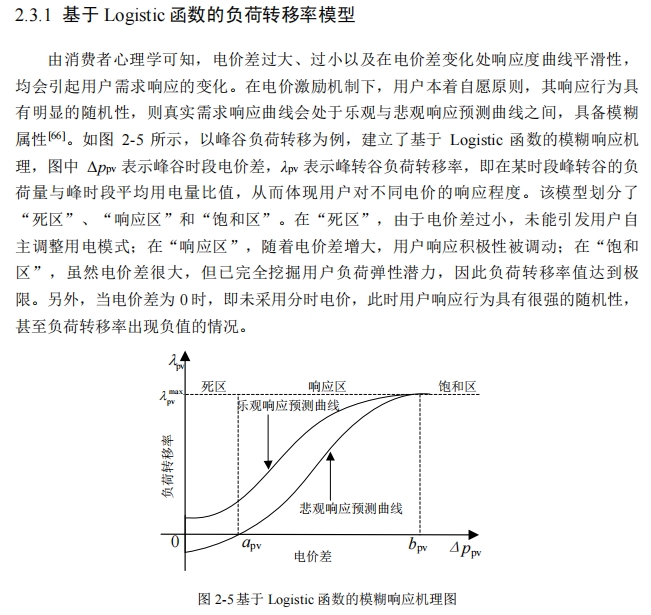
Logistic函数因其S型曲线特性，能够很好地描述用户响应意愿随激励强度（价差）增加而先缓慢上升、后快速上升、最终趋于饱和的心理过程。

3. 综合响应率的动态融合

模型引入一个模糊隶属度 m 来衡量当前价差在预设区间 [apv, bpv] 中的位置。该隶属度决定了乐观与悲观响应率的加权方式：

当价差过小（Δprice ≤ apv）：激励不足，用户几乎无响应，采用乐观与悲观响应率的简单平均值。
当价差处于中等水平（apv < Δprice ≤ bpv）：用户响应意愿随价差增大而增强，综合响应率在悲观值与平均值之间动态调整。
当价差足够大（Δprice > bpv）：激励效果充分，用户响应接近乐观预期，直接采用乐观响应率。

通过这种方式，模型避免了单一响应率的僵化，能够更细腻地刻画用户行为随激励强度变化的非线性特征。

4. 负荷转移量计算与新负荷曲线生成

在分别计算出“峰转平”、“峰转谷”和“谷转平”三种路径的综合响应率后，模型执行以下步骤：

时段分类：遍历24小时，根据电价序列 dj 将原始负荷 pload1 分类为谷段负荷、平段负荷和峰段负荷。
计算平均负荷：分别求出谷段、平段、峰段的平均负荷值，作为负荷转移的基准量。
计算负荷调整量 q：对于每一个时段 t：
如果是平段，负荷将减少，减少量由“峰转平”和“谷转平”两部分转移量共同决定。
如果是峰段，负荷将增加（来自峰段自身削减）并减少（转移出去），净调整量是两者的综合结果。
* 如果是谷段，负荷将增加，增加量由“峰转谷”和“谷转平”的反向转移量构成。
生成新负荷曲线：将原始负荷 pload1 与调整量 q 相加，得到实施需求响应后的新负荷曲线 pload2。

5. 结果可视化

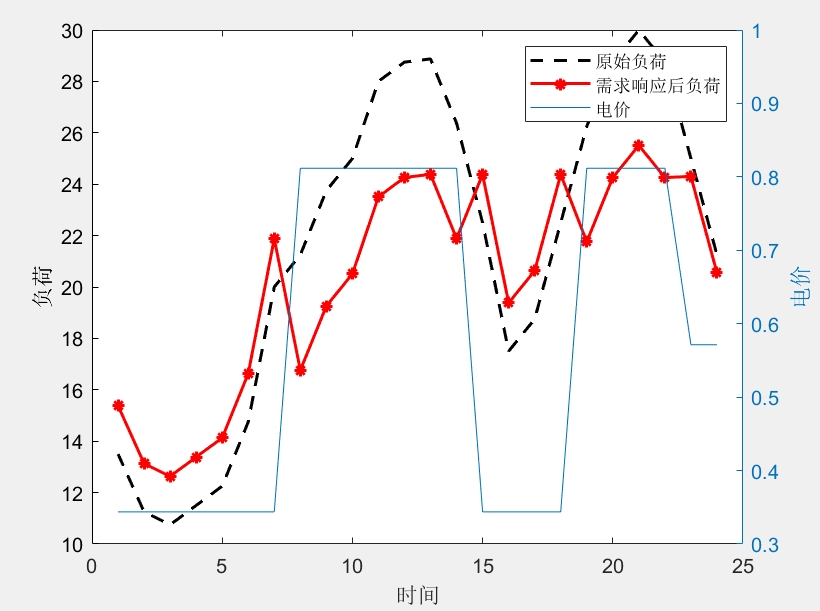
最后，代码通过绘图直观地对比了需求响应前后的负荷曲线，并在同一图中展示了分时电价的变化，清晰地呈现了电价信号如何有效引导负荷从高峰时段向平、谷时段转移，从而达到“削峰填谷”的优化目标。

总结

该需求响应模型通过融合用户心理预期的边界情景与Logistic函数的非线性特性，构建了一个灵活且贴合实际的负荷转移模拟框架。其核心优势在于能够动态适应不同的电价激励强度，为电网运营商或售电公司制定更精准、更有效的电价策略提供了有力的量化分析工具。此实现为负荷侧资源的精细化管理和电力市场的高效运行奠定了坚实的技术基础。