上一篇:凸函数总结
函数 的图像定义为
的图像定义为
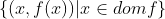 ,
,
它是空间的一个子集。函数
 的上境图定义为
的上境图定义为
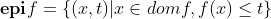 ,它也是
,它也是空间的一个子集。
定理 函数 是凸函数当且仅当
是凸函数当且仅当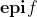 是凸集。
是凸集。
证明:
(必要性)显然成立,证明省略。
(充分性)假设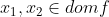 ,显然有
,显然有,又由于
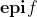 是凸集
是凸集
所以有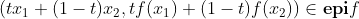 即得
即得
 成立,由于
成立,由于 的任意性可知
的任意性可知 是凸函数。
是凸函数。
亚图
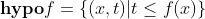 ,
,
类似上述定理有函数 是凹函数当且仅当其亚图是凸集。
是凹函数当且仅当其亚图是凸集。
上一篇:凸函数总结
函数 的图像定义为
的图像定义为
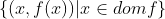 ,
,
它是空间的一个子集。函数
 的上境图定义为
的上境图定义为
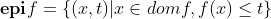 ,它也是
,它也是空间的一个子集。
定理 函数 是凸函数当且仅当
是凸函数当且仅当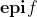 是凸集。
是凸集。
证明:
(必要性)显然成立,证明省略。
(充分性)假设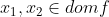 ,显然有
,显然有,又由于
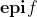 是凸集
是凸集
所以有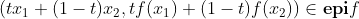 即得
即得
 成立,由于
成立,由于 的任意性可知
的任意性可知 是凸函数。
是凸函数。
亚图
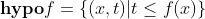 ,
,
类似上述定理有函数 是凹函数当且仅当其亚图是凸集。
是凹函数当且仅当其亚图是凸集。
 2224
2224
 274
274

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


