云安全定量评估方法研究

云安全的定量评估方法

1 引言

随着全球计算机技术的快速发展，云计算技术已成为新一轮技术革命的关键，并广泛应用于政府、企业、教育、数据中心等领域[1]。云平台为用户提供了服务便利、存储空间和计算能力的快速扩展以及更低的部署成本。然而，采用云计算意味着用户的核心数据和业务脱离了自身的控制，因此云平台的安全问题受到广泛关注[2, 3]。云计算平台突破了传统信息系统的边界，在共享IT基础设施上运行，这意味着基于边界防护的传统安全评估方法已无法发挥作用[4, 5]。

如何评估云计算平台的安全性，并为用户提供可量化的可评估指标，已成为重要的研究课题。近年来，针对云平台的安全防护技术，特别是数据安全技术，已成为国内外研究人员的关注焦点[6]，云平台整体安全的评估方法也引起了研究人员的兴趣[4, 7]。然而，由于云安全相关标准尚未建立，目前仍未找到被广泛认可的云安全评估方案。

云安全领域目前缺乏系统的评估和定量方法。基于云计算平台的特点，本文提出了一种建立云计算安全指标评估体系的方法。该体系利用模糊隶属函数表达主观评价元素，并采用G.A. 米勒理论对云计算平台的整体安全性进行量化。此外，文章中的示例展示了评估云平台安全性的完整流程，证明了该方法对建设者和用户具有可操作性。

2 相关工作

云计算平台通过互联网提供动态且可扩展的虚拟资源。凭借分布式计算、并行处理、存储和强大计算能力的特点，它属于大数据时代特定的信息系统模式。

然而，尽管云计算技术提供了便捷的服务，云安全问题也日益突出，制约了云计算技术的深入发展。目前已有大量关于云计算安全问题的研究工作。例如，冯等人[2]认为在云计算平台中应考虑安全问题；陈等人[1]提出了一套更为全面的云计算安全体系；林等人[3]则提出了一种云计算安全架构。

另一方面，为了提高信息和网络安全，我们建立了信息安全等级体系，并制定了一系列安全标准。然而，该安全等级体系主要针对传统信息系统的问题，未涉及云计算平台的边界模糊问题。也有一些研究工作考虑了云平台的特殊性来探讨安全评估方案。例如，陈等人[4]提出了基于等级保护的安全评估方法；江[7]构建了基于等级保护的安全评估模型。然而，这些评估方法通常侧重于如何使云评估与现有评估体系相兼容，未能提出适用于云平台安全评估的合适且可量化的评估方法。

因此，本文提出了一种针对云计算平台的指标体系，以及量化表达指标和整体方法论。该论文中的方法对评估云计算安全具有积极作用，并帮助用户选择合适的云服务，从而促进云计算产业的健康发展。

3 云计算安全指标体系

在云计算安全指标体系中，可以采用定性评估方法。首先可以使用列表记录所有需要评估的云计算安全指标，然后逐一审查这些指标。如果所有指标均满足基准要求，则测试通过。如果未满足要求，则需要进一步的证据。需要注意两点：（1）指标权重问题：不同类型的指标在安全中的重要程度不同。（2）指标评估结果：如果在安全指标评估中应用二值逻辑来判断结果，意味着安全评估只能是“通过”或“不通过”。但实际上，很少有指标完全符合标准或完全不符合标准。即使所有指标都被判定为“通过”，被测对象在安全性能上也存在差异，而二值逻辑的评估结果无法反映这些差异。

为了解决指标权重差异和评估过程控制的问题，我们提出了一种更全面的解决方案。所包含的方法——在云计算安全评估中选取连续范围内的数值——是一种比二值逻辑评估更客观的模糊评估方法。

3.1 指标体系构建原则

云安全指标体系的设计原则包括：（1）科学性：指标的选取基于云计算安全研究，符合相关法律法规。（2）层次性：云计算安全指标体系应根据不同属性划分为不同层级。（3）独立性：安全指标能够单独反映云计算的安全状况。（4）可操作性：云计算安全指标体系应客观实用，满足实际安全评估的需求。（5）系统性：需要考虑平台的各种因素，反映整体系统的内部关系。

3.2 指标体系的架构

云计算安全指标体系的构建过程包括：（1）根据国内外专家意见，结合实际情况，设计关于云计算安全评估指标体系的调研表，然后利用这些调研表收集专家提出的云计算平台安全指标。（2）通过调研表的反馈，可以获得专家认可的云计算安全指标。（3）重复前述两个步骤，直到大多数专家达成符合原则的安全指标体系。

云计算安全指标体系包括：技术指标体系和管理指标体系。技术安全指标体系包括：物理安全、网络安全、主机系统安全、应用安全、数据安全、备份与恢复等指标。管理安全指标体系包括：安全管理体系、安全管理、安全人员管理、建设管理和系统运行、维护管理等指标。这些指标体系涵盖了云计算安全评估的需求。

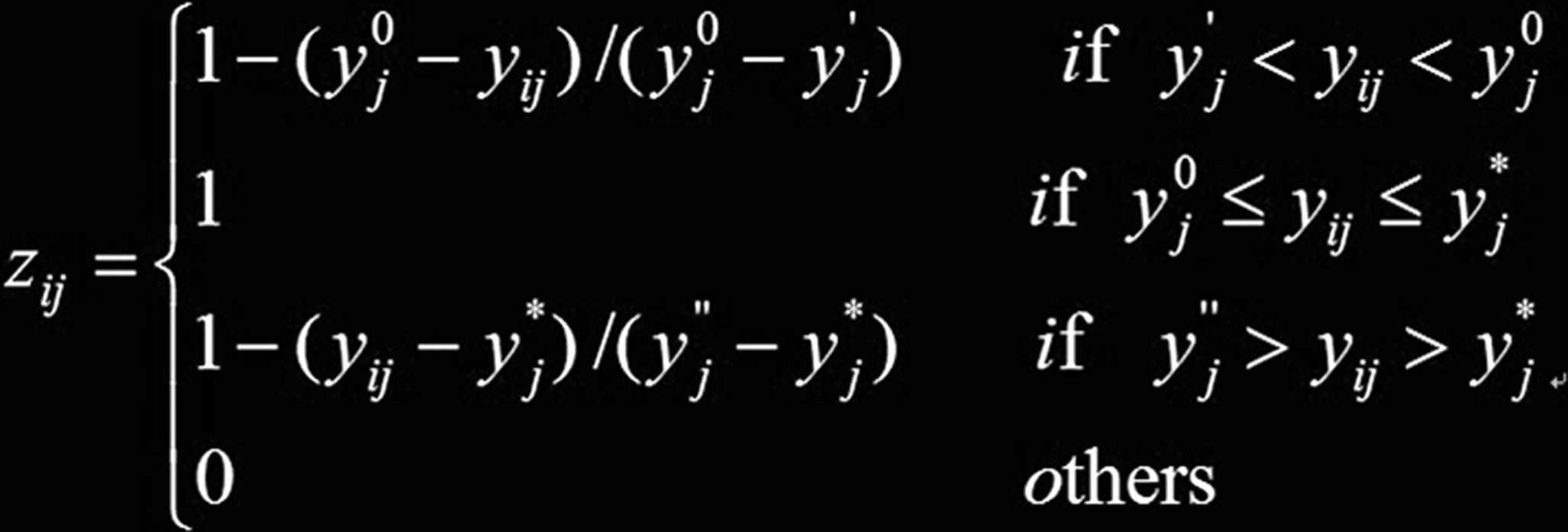
4 云安全的定量评估

云计算安全的定量评估具有很强的主观性，且“符合”与“不符合”之间没有绝对界限，通常采用模糊方法。模糊评价有助于表述安全问题。我们可以根据实际情况将整体问题分解为若干小问题，以便评估人员进行主观评价。评估人员作出类似百分比形式的模糊判断，能更准确地反映云安全状况。模糊评估方法是将模糊数学理论应用于云安全概率的量化[8, 9]。该概率可视为模糊数，通过建立云安全事件树并结合三角模糊树、LR模糊数等进行定量分析。然而，该评估方法依赖于评估人员对评价等级和权重的主观选择，因此其结果的科学性和客观性需要进一步验证。

为了确保客观评估，约桑的主观逻辑评价方法也为描述主观行为提供了有效途径，但该方法仍然过于依赖主观判断，其正确性值得怀疑。为解决上述问题，我们决定采用多属性决策方法对云平台安全进行定量评估，综合考虑云平台安全评估定量分析的三个特点——无统一的无量纲指标、覆盖范围广以及互斥性。关于云平台安全定量评估的多属性决策方法有多种：乐观型、悲观型、乐观‐悲观联合型、简单加权平均、折衷法。其中，折衷决策倾向于尽可能接近理想解，或尽可能远离负理想解，并在理想解与负理想解之间寻找一个相对满意的可行解。关键在于如何选择基准，以及如何衡量可行解与基准之间的距离，以满足安全定量评估的要求。

4.1 多属性决策指标体系

云计算平台是由相互作用的子系统构成的复杂系统。因此，对云平台的安全评估需要多个相互关联的评价指标。根据层次结构，这些指标被组合成一个具有特定评估功能的整体。该指标体系包括：经济指标、技术指标、资源指标、基础设施指标等。

4.2 决策指标的规范化

确定指标的成本效益值。 例如，随着云计算平台安全指数的数据共享率不断提高，资源利用率得到提升且成本降低，但同时也会带来安全性降低。因此，数据共享率必须被限制在适当范围内。

指标的无量纲化。 云计算平台安全评估的最大问题在于指标之间的不可公度性，换句话说，属性值列表中每一列的属性值具有不同的量纲，一旦对同一属性采用不同的计量单位，列表中的数值就会变得不同。

归一化思想。 在原始属性值列表中，不同指标的属性值量级差异很大。为了使用多目标评价方法对这些值进行比较，必须对属性值列表的值进行归一化，即将数值平移至区间[0, 1]。同时，在预处理数据时采用非线性变换方法解决不完全补偿性问题。

指标归一化方法：

（1）线性缩放变换。效益型属性：变换后最差值属性为 0，最优值为1。成本导向属性：变换后最差值属性为1，最优值为0。

（2）标准 0–1变换。对于每个属性，最优值为1，最差值为0，且变换后的差异是线性的。

（3）最优值在区间之间的变换。给出具体属性区间以便于判断。

（4）向量归一化。规范化后，同一指标各方案的属性值平方和为“1”，无论成本导向或效益导向类型，属性值的量级无法区分。

（5）定性指标的量化方法。某些指标为定性类型，只能进行定性描述。例如云平台安全指标的可靠性。将定性指标量化，将这些指标划分为若干等级，并赋以不同数值。

4.3 多属性决策

1. 多属性决策准备工作

(1) 决策矩阵 假设：
备选方案集为：$ X = {X_1, X_2, \dots, X_m} $；
方案的属性集为：$ Y = {y_1, y_2, \dots, y_n} $

(2) 决策矩阵定义为：
$$
Y =
\begin{bmatrix}
y_{11} & \cdots & y_{1n} \
\vdots & \ddots & \vdots \
y_{i1} & \cdots & y_{ij} & \cdots & y_{in} \
\vdots & \ddots & \vdots \
y_{m1} & \cdots & y_{mn}
\end{bmatrix}
$$

2. 数据预处理

(1) 线性变换
原始决策矩阵为 $ Y = {y_{ij}} $，经过变换后变为 $ Z = {z_{ij}} $，其中 $ i = 1,\dots,m $，$ j = 1,\dots,n $。假设 $ y_j^{\text{max}} $ 为矩阵第j列的最大值，

若 $ j $ 为效益型属性，则：
$$
z_{ij} = \frac{y_{ij}}{y_j^{\text{max}}} \tag{1}
$$
预处理数据时，最差值属性在变换后不一定为0，但最优值是1。

如果 $ j $ 是成本导向属性，则可以设置：
$$
z_{ij} = 1 - \frac{y_{ij}}{y_j^{\text{max}}} \tag{2}
$$
经过（2）变换后，最优属性值不一定为1，最差为0。成本导向属性可使用以下公式进行变换：
$$
z_{ij} = \frac{y_j^{\text{min}}}{y_{ij}} \tag{3}
$$
在使用（3）公式进行变换后，最差值不一定为0，最优值为1，且属于非线性变换。

(2) 0–1标准变换。
对于线性变换，经过线性变换后，如果属性j的最优值为1，则其最差值通常不是0；如果最差值为0，则最优值通常不是1。经过平移后，当属性的最优值为1且最差值为0时，可进行标准0–1变换。对于效益型属性j，设：
$$
z_{ij} = \frac{y_{ij} - y_j^{\text{min}}}{y_j^{\text{max}} - y_j^{\text{min}}} \tag{4}
$$
当j为成本导向属性时，设置：
$$
z_{ij} = \frac{y_j^{\text{max}} - y_{ij}}{y_j^{\text{max}} - y_j^{\text{min}}} \tag{5}
$$

(3) 最优值给定区间的平移。
文章设定了最优属性区间$[y_j^0, y_j^ ]$，其中$y_j’$为不可容忍下限，$y_j’‘$为不可容忍上限，然后：
$$
z_{ij} =
\begin{cases}
0, & y_{ij} \leq y_j’ \
\frac{y_{ij} - y_j’}{y_j^0 - y_j’}, & y_j’ < y_{ij} \leq y_j^0 \
1, & y_j^0 < y_{ij} \leq y_j^ \
\frac{y_j’’ - y_{ij}}{y_j’’ - y_j^ }, & y_j^ < y_{ij} < y_j’’ \
0, & y_{ij} \geq y_j’‘
\end{cases} \tag{6}
$$
属性值$z_{ij}$与原始$y_{ij}$之间的函数图像为梯形。

（4）向量归一化。该方法中的成本导向或效益型属性，均可采用以下公式进行转换：
$$
z_{ij} = \frac{y_{ij}}{\sqrt{\sum_{i=1}^{m} y_{ij}^2}} \tag{7}
$$
变换是线性的，因此无法区分变换后属性值的量级。规范化后，所有方案中同一属性值的平方和为1，通常用于计算所有方案与某个虚拟方案之间的欧氏距离。

（5）原始数据统计处理方法。
对于原始数据，通过统计平均法进行预处理。设M为百分制均值。将M设为方案集X的属性均值，然后使用以下公式进行转换：
$$
z_{ij} = \left( \frac{y_{ij} - \bar{y} j}{y_j^{\text{max}} - \bar{y}_j} \right)(1.00 - M) + M \tag{8}
$$
在公式中，$\bar{y}_j = \frac{1}{m} \sum {i=1}^{m} y_{ij}$是所有方案中属性j的均值，m为方案的数量，M的取值在0.5到0.75之间。

(6) 专家打分数据的预处理。
由于性能指标难以通过统计数据进行测量，通常会邀请专家对评价对象进行评分，并将评分均值作为相关指标的属性，以此来确定对象的状态。
鉴于专家意见可能存在差异，专家的意见也是评估的关键。在本文中，所有专家的评分都被标准化到同一区间$[M_0, M_ ]$内。不同的$M_0$和$M_ $不会影响结果，只要评分处于上述区间即可。具体算法如下：
$$
z_{ij} = M_0 + (M_ - M_0) \cdot \frac{y_{ij} - y_j^{\text{min}}}{y_j^{\text{max}} - y_j^{\text{min}}} \tag{9}
$$
当$M_0 = 0$、$M_ = 1$时，上述算法与效益型属性0–1变换公式（4）相同。

3. 基于最大化偏差的多属性决策方法

对于多属性决策问题，若权重信息未知且决策矩阵为 $ A = (a_{ij}) {n \times m} $，当对 $ A $ 进行标准化处理时，可得到标准化矩阵 $ R = (r {ij})_{n \times m} $

假设属性的权重向量为 $ w = (w_1, w_2, \dots, w_m) $，$ w_j \geq 0 $，$ j \in M $，并满足约束条件：
$$
\sum_{j=1}^{m} w_j^2 = 1 \tag{10}
$$
然后，每个方案的属性值可以定义为：
$$
z_i(w) = \sum_{j=1}^{m} r_{ij} w_j \tag{11}
$$
多属性决策是对所有方案的属性值排序进行比较。方案间$u_j$的差异越小，该属性对方案决策和排序的作用越弱；反之，方案间$u_j$的差异越大，该属性对方案决策和排序的作用越强。

从对所有方案进行排序的角度来看，本文可以得出结论：方案的属性值偏差越大，所赋予的权重就越大。如果所有方案的属性之间没有差异，则属性 $ u_j $ 对方案排序没有影响，其权重为 0。

5 定量分析示例

5.1 安全评估模块

该评估模块包含多属性决策方法，用于获取云平台的属性权重、方案偏好和决策权重。其中，基于多属性决策方法的属性特征，对云平台的安全属性权重进行多属性决策，并从两个方面对云平台的安全属性进行分类。首先，将云平台的安全属性分为定量类型和定性类型；其次，可分为效益导向型和成本导向型。其中，效益型属性的值越大越好，对评估结果具有正向影响；而成本型属性的值越小越好，对评估结果具有负向影响。本文提出的评估属性属于效益型属性和定量类型属性。方案偏好用于衡量决策者对方案和属性的偏好、属性重要性以及与方案相关的决策者权威性（权威系数）。通常使用区间数表示决策权重，可定义区间数的期望值，通过最小化方案评估值与期望值之间的差异，确保权重向量选择的客观性。

5.2 量化评估

云安全量化评估算法的步骤包括：（1）对云平台量化评估的属性进行模糊化处理，使用G. A. 米勒理论构建区间值形式较为实用，最终形成决策矩阵。（2）利用公式对云平台安全量化评估的归一化决策矩阵进行归一化处理。（3）根据专家对云平台安全量化评估的偏好水平和经验，确定各属性的期望值。（4）获取云平台安全量化评估的属性权重。（5）最后，计算各评估方案的属性值根据权重进行相应排序。（6）为验证模型的可用性，可对专家开展相关问卷调查，并通过聚合得到云计算量化评估方案（表1）。

（1）属性量化与规范性方法。
上述表格中定量属性值的规范性方法，结果如表2所示。
该文章对成本导向和效益导向属性进行了规范化，从而得到如下标准规范的决策矩阵：

表 1. 云计算安全量化评估的定量属性特征

评估方法	物理安全	Host 安全	应用程序 安全	Data 安全	管理
X1	不错	Bad	Good	Good	Good
X2	优秀	优秀	非常差	不错	不错
X3	不错	不错	优秀	Good	Good
X4	优秀	优秀	Bad	不错	不错
X5	非常差	poor	不错	Good	Good

表 2. 云计算安全量化评估指标的规范方法

评估方法	物理安全	Host 安全	应用程序 安全	Data 安全	管理
X1	[0.322 0.412]	[0.174 0.203]	[0.542 0.633]	[0.393 0.481]	[0.595 0.774]
X2	[0.522 0.656]	[0.561 0.618]	[0.129 0.181]	[0.268 0.330]	[0.174 0.207]
X3	[0.511 0.574]	[0.381 0.511]	[0.595 0.707]	[0.395 0.454]	[0.414 0.449]
X4	[0.548 0.631]	[0.522 0.588]	[0.127 0.169]	[0.327 0.357]	[0.214 0.263]
X5	[0.158 0.222]	[0.071 0.093]	[0.412 0.462]	[0.580 0.692]	[0.478 0.571]

（2）确定专家对每个云安全量化评估方案的主观判断和偏好。
例如，一些专家参与了云平台安全性的评判，权威性为 $ b’_p = (0.83, 0.74, 0.80, 0.94) $，属性重要度为 $ W_j = (0.25, 0.28, 0.15, 0.21, 0.11) $。根据本文所述公式，可获得专家对不同云安全量化评估方案的偏好。

(3) 选择客观属性的综合评价和最优权重值
本文根据不同参数分配$W_j$，然后参照不同参数的属性最优权重比较云平台安全等级（表 3）。
选择不同参数时权重分配存在差异。原因是随着权重的增加，专家的主观判断信息在模型中的作用逐渐放大，对云平台的量化结果影响最大。然而，由于模型的变换，其他属性的分配也发生了一些变化。

表3. 云计算安全的量化评估结果

模型 参数 a, b	属性优化权重 $W_j$	方案属性$Z_j$的综合值
a = 1.0, b = 0 (模型P1)	(0.37, 0.15, 0.12, 0.22, 0.14)	(0.4344, 0.4398, 0.4906, 0.4269, 0.3477)
a = 0.5, b = 0.5 (模型P1&P2)	(0.34, 0.19, 0.13, 0.18, 0.16)	(0.4215, 0.4438, 0.5060, 0.4247, 0.3347)
a = 0, b = 1（模型 P2）	(0.41, 0.13, 0.14, 0.21, 0.11)	(0.4205, 0.4430, 0.5004, 0.4312, 0.3403)

6 总结

综上所述，本文采用多属性决策方法对云计算安全进行评估，不仅确立了属性的权重，还综合考虑了专家对评估方案的偏好和客观最优排序两个因素。这是对模糊评估方法和主观逻辑评估方法的优化与改进，确保属性权重能够真实反映云平台的安全状况，为云计算的量化评估提供了高效实用的方法。