龙格库塔法比欧拉法有更高的精度。
Runge-Kutta Ansatz
Δ
y
(
t
)
=
a
∗
f
(
t
,
y
)
+
b
∗
f
(
t
+
α
h
,
y
+
β
f
)
(
a
,
b
,
α
,
β
i
s
f
r
e
e
p
a
r
a
m
e
t
e
r
s
)
=
a
f
+
b
f
+
b
(
f
t
α
+
f
y
f
β
)
h
:
=
h
f
+
h
2
2
(
f
t
+
f
y
f
)
\Delta y(t)=a*f(t,y)+b*f(t+\alpha h, y+\beta f) \quad (a, b, \alpha, \beta \quad is free parameters)\\ = af+bf+b(f_t\alpha+f_yf\beta)h\\ :=hf+\frac{h^2}{2}(f_t+f_yf)
Δy(t)=a∗f(t,y)+b∗f(t+αh,y+βf)(a,b,α,βisfreeparameters)=af+bf+b(ftα+fyfβ)h:=hf+2h2(ft+fyf)
其中
a
+
b
=
h
a+b=h
a+b=h,
α
b
=
h
2
\alpha b=\frac{h}{2}
αb=2h,
β
b
=
h
2
\beta b=\frac{h}{2}
βb=2h。
时间复杂度
O ( h 4 ) O(h^4) O(h4)。
C++ 实现 4 4 4 阶 RK
输入参数
类似欧拉法。
f ′ ( x ) f'(x) f′(x) 函数
类似欧拉法,采用外部函数的方式,定义好接口,每个具体问题具体实现。由于 RK 需要计算 k 1 , k 2 , k 3 , k 4 k_1, k_2, k_3, k_4 k1,k2,k3,k4,因此 RK 的函数原型对应如下。
//x,y 表示对应的坐标
//h 为步长
//k 为返回值,一个4大小的数组
void df(double x, double y, double h, double k[]);
主框架
参考欧拉法实现。
#include <iostream>
using namespace std;
/*f'(x)函数*/
//x,y 表示对应的坐标
//h 为步长
//k 为返回值,一个4大小的数组
void df(double x, double y, double h, double k[]);
int main() {
//变量定义
double x0, y0;//起点坐标
double xn;//终点坐标
int step;//迭代次数
cout<<"Enter Initial Condition x0:";
cin>>x0;
cout<<"Enter Initial Condition y0:";
cin>>y0;
cout<<"Enter calculation point xn:";
cin>>xn;
cout<<"Enter number of steps:";
cin>>step;
double delta;//x的增量
delta=(xn-x0)/step;
/* Runge Kutta Method */
double yn;
double k[4];
cout<<"Step:\tx0\ty0\t\tyn\n";
cout<<"-----------\n";
for (int i=1; i<=step; i++) {
df(x0, y0, delta, k);
yn=y0+(k[0]+2*k[1]+2*k[2]+k[3])/6;
cout<<i<<":\t"<<x0<<"\t"<<y0<<"\t"<<yn<<"\n";
x0=x0+delta;
y0=yn;
}
//结果输出
cout<<"\nValue of y at x= "<<xn<<" is " <<yn<<"\n";
return 0;
}
样例
样例 1
给定 d y d x = y 2 − x 2 y 2 + x 2 \frac{dy}{dx}=\frac{y^2-x^2}{y^2+x^2} dxdy=y2+x2y2−x2,初始条件为 y ( 0 ) = 1 y(0)=1 y(0)=1,计算 y ( 0.6 ) y(0.6) y(0.6) 的值,用 3 3 3 步。
f ′ ( x ) f'(x) f′(x) 函数实现
static double df1(double x, double y) {
return (y*y-x*x)/(y*y+x*x);
}
//x,y 表示对应的坐标
//h 为步长
//k 为返回值,一个4大小的数组
void df(double x, double y, double h, double k[]) {
k[0]=h*df1(x, y);
k[1]=h*df1(x+h/2, y+k[0]/2);
k[2]=h*df1(x+h/2, y+k[1]/2);
k[3]=h*df1(x+h, y+k[2]);
}
编译
测试环境为 Win10+MinGW,使用 g++ 编译器。
g++ -g -o RK.exe main.cpp df1.cpp
计算机输出
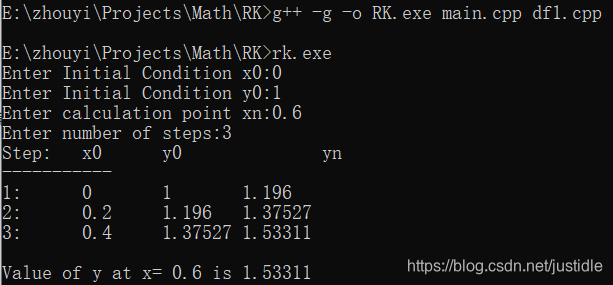
 龙格库塔法解析
龙格库塔法解析





 本文介绍了数值解常微分方程中龙格库塔法的基本原理及其C++实现过程。对比欧拉法,龙格库塔法具有更高的精度。文章详细展示了4阶龙格库塔法的具体步骤,并通过一个实例说明了如何应用该方法进行计算。
本文介绍了数值解常微分方程中龙格库塔法的基本原理及其C++实现过程。对比欧拉法,龙格库塔法具有更高的精度。文章详细展示了4阶龙格库塔法的具体步骤,并通过一个实例说明了如何应用该方法进行计算。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










