SSE图像算法优化系列2-高斯滤波

PS

这篇文章似乎写歪了啊，因为我测试SSE优化的代码，发现和原始版本的C代码速度是一致？不知道是有什么核心的地方没注意到？我再研究研究吧。

前言

本算法的原理以及优化过程都是偷师ImageShop，也可以把这篇文章理解为https://www.cnblogs.com/Imageshop/p/6376028.html 这篇文章的一篇阅读总结。

原理

首先，高斯滤波是可以用递归算法来实现的。这最早见于《Recursive implementation of the Gaussian filter》论文中：
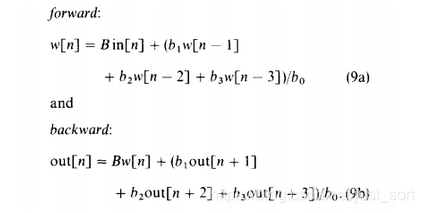在forward的过程中，n是递增的，所以，我们在进行forward之前将in数据复制给w，然后上式即可变形为：
$w[n]=Bw[n]+(b_{1}w[n-1]+b_{2}w[n-2]+b_{3}w[n-3])/b_0$-------(1a)。
同理backward过程中n是递减的，因此在backward前将w的数据完整的拷贝到out中，则式9b则变为:
$out[n]=B$