OpenCV图像处理专栏七 | 直方图均衡化算法及代码实现

前言

这是OpenCV图像处理专栏的第七篇文章，主要为大家介绍一下直方图均衡化算法的原理以及提供一个我的C++代码实现。

介绍

直方图均衡化，是对图像进行非线性拉伸，使得一定范围内像素值的数量的大致相同。这样原来直方图中的封顶部分对比度得到了增强，而两侧波谷的对比度降低，输出的直方图是一个较为平坦的分段直方图。具体来讲可以表现为下面这个图：

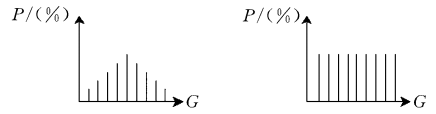
通过这种方法可以按照需要对图像的亮度进行调整，并且，这种方法是可逆的，也就是说知道了均衡化函数，也可以恢复原始的直方图。

算法原理

设变量$r$代表图像中像素灰度级。对灰度级进行归一化处理，即$0<=r<=1$，其中$r=0$表示黑，$r=1$表示白。对于一幅给定的图片来说，每个像素在$[0,1]$的灰度级是随机的，用概率密度$p_r(r)$来表示图像灰度级的分布。为了有利于数字图像处理，引入离散形式。在离散形式下，用$r^k$代表离散灰度级，用$p_r(r^k)$代表$p_r(r)$，并且下式子成立：$P_r(r^k)=\frac{n^k}{n}$，其中$0<=r^k<=1,k=0,1,2,...,n-1$。式子中$n^k$代表图像中出现$r^k$这种灰度的像素个数，$n$是图像的总像素个数，图像进行直方图均衡化的函数表达式为:$S_i=T(r_i)={\sum }_{i=0}^{k-1}\frac{n_i}{n}$，式子中，$k$为灰度级数(RGB图像为255)。相应的反变换为$r^i=T^{-1}(S_i)$

代码实现

//直方图均衡化
Mat Histogramequalization(Mat src) {
    int R[256] = {0};
    int G[256] = {0};
    int B[256] = {0};
    int rows = src.rows;
    int cols = src.cols;
    int sum = rows * cols;
    //统计直方图的RGB分布
    for (int i = 0; i < rows; i++) {
        for (int j = 0; j < cols; j++) {
            B[src.at<Vec3b>(i, j)[0]]++;
            G[src.at<Vec3b>(i, j)[1]]++;
            R[src.at<Vec3b>(i, j)[2]]++;
        }
    }
    //构建直方图的累计分布方程，用于直方图均衡化
    double val[3] = {0};
    for (int i = 0; i < 256; i++) {
        val[0] += B[i];
        val[1] += G[i];
        val[2] += R[i];
        B[i] = val[0] * 255 / sum;
        G[i] = val[1] * 255 / sum;
        R[i] = val[2] * 255 / sum;
    }
    //归一化直方图
    Mat dst(rows, cols, CV_8UC3);
    for(int i = 0; i < rows; i++){
        for(int j = 0; j < cols; j++){
            dst.at<Vec3b>(i, j)[0] = B[src.at<Vec3b>(i, j)[0]];
            dst.at<Vec3b>(i, j)[1] = B[src.at<Vec3b>(i, j)[1]];
            dst.at<Vec3b>(i, j)[2] = B[src.at<Vec3b>(i, j)[2]];
        }
    }
    return dst;
}

效果

原图

直方图均衡化后的图

后记

本文为大家介绍了直方图均衡化算法，以及它的简单代码实现，希望可以帮助到你。

---

欢迎关注我的微信公众号GiantPandaCV，期待和你一起交流机器学习，深度学习，图像算法，优化技术，比赛及日常生活等。