微分方程:凡含有参数,未知函数和未知函数导数 (或微分) 的方程,称为微分方程,有时简称为方程,未知函数是一元函数的微分方程称作常微分方程,未知函数是多元函数的微分方程称作偏微分方程。微分方程中出现的未知函数最高阶导数的阶数,称为微分方程的阶(order)

Ordinary Differential Equation常微分方程(ODE)
若未知函数是一元函数的微分方程称为常微分方程。一般的 n 阶常微分方程的形式(也称隐式表达式)。可以看到全部都是一元函数的导数和自变量x,没有出现(xy)'的多元函数导数,注意一元函数可以是高幂的函数

separable differential equations 可分离的微分方程
常微分方程通常可以用分离变量法解出通解,但可分离变脸的不一定是常微分方程

通过将变量分离到方程两边,即将与 yy 有关的项放在一边,与 xx 有关的项放在另一边,最后可以对两边分别积分来求解


Exponential growth model
指数增长,一定是增长率与一个也不断增长的东西有关kp,t是线性变化,如果dp/dt = kt就不可能是指数变化。重点是increasing / decreasing exponential 后面的with不重要,因为一定是dy/dt = kp(增长就是+p,减小就是-p)



![]()
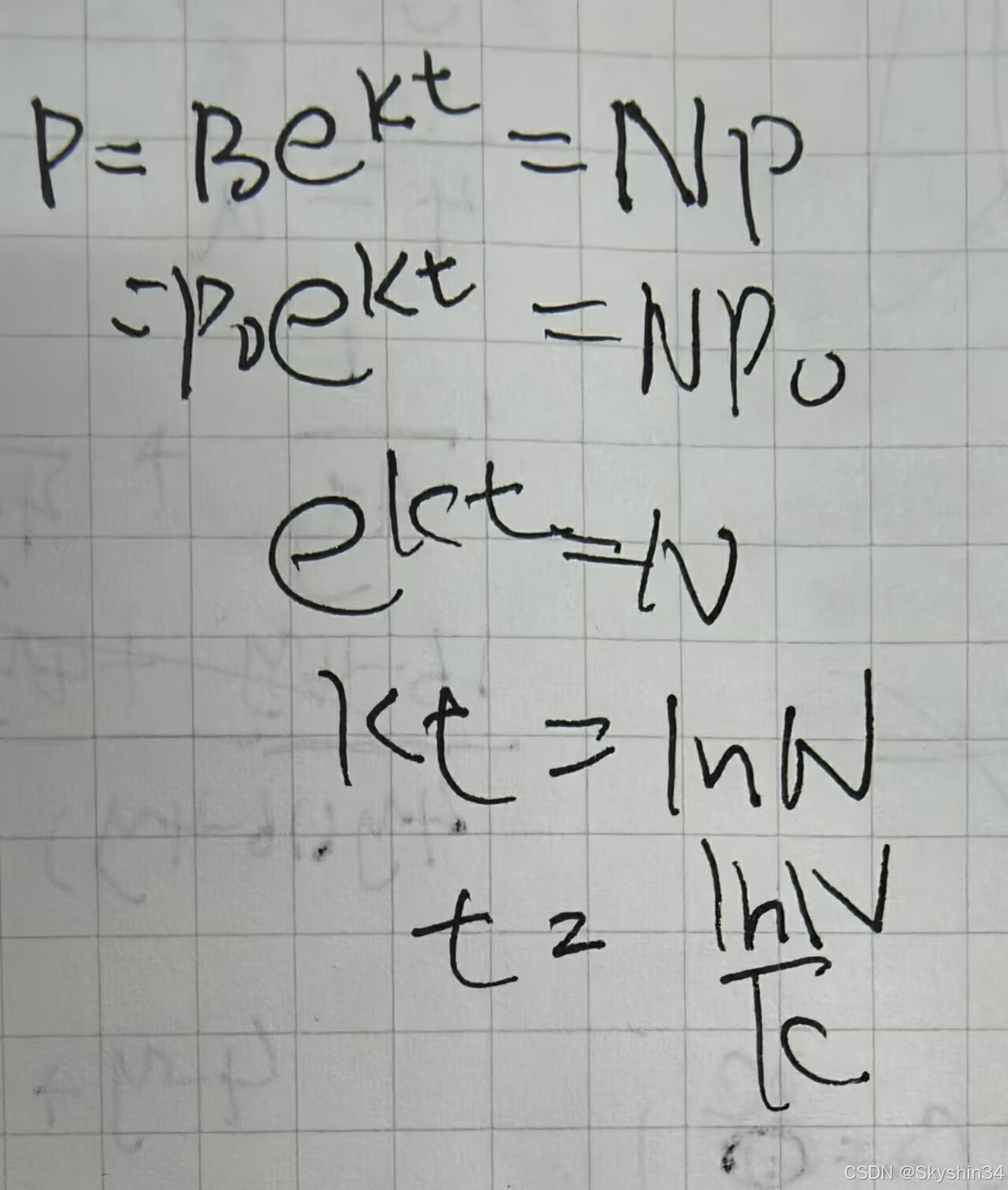

计算倍数,需写成通解形式
First-order Autonomous ODEs 一阶自治(常)微分方程
常微分方程的一种,等式中没有自变量


其中y在应用中会被其他变量影响,比如后面提到的指数增长模型


无解的一阶自治微分方程,看微分方程解的性质:
平衡解正是当y取某些值时,方程的解不再随t变换而变化
y与x无关,y的导数也就与x无关。
相直线,广义线性回归增长模型-Logistic模型





完整分析一个一阶自治微分方程
Equilibrium solution 平衡点 : stable稳定/unstable不稳定/semistable半稳定解
函数的导数值为0的x值称之为critical point,但![]() 即使自治微分方程导数值为0的y值称之为平衡点/静止点
即使自治微分方程导数值为0的y值称之为平衡点/静止点



\
 如果微分方程含x项,则会在X轴某处平衡,其他部分依然不平衡
如果微分方程含x项,则会在X轴某处平衡,其他部分依然不平衡
 对于方程,绝对值需要拆开,当y大于5时为(y-5)y小于5为(5-y)
对于方程,绝对值需要拆开,当y大于5时为(y-5)y小于5为(5-y)
不能认为永远大于0

Direction Field 方向场
相直线只是描述微分方程的解-函数大概的趋势,并不能精确描述函数的性质。为了精确描述的特征,并且可以解决一些我们无法用分离变量找到原函数(解)的微分方程,我们通过方向场



Modeling with ODEs: Variations of exponential growth/decay model 指数增长/衰减模型的变体
该模型的特点为:变量的变化率与变量自身的值成比例
在数学上通过特定的微分方程来描述:将一阶自治微分方程的右侧的f(y)设为ky。用分离变量求y可得为指数函数,讨论K取不同值的图像


变体形式:将y(t)设为k(y-Y),其中Y是常数,由此我们知道该一阶自治方程的平衡点是Y

本例微分方程可解,所以我们求出可分离变量的微分方程通解来验证我们对解性质描述的图像

接下来看指数增长/衰减模型如何运用在生活中:
e.g.1 Newton’s law of cooling
加热和冷却模型, 加热物体放置一段时间后,会随着周围介质中热量的散失而冷却。
物体的温度降低,最终达到周围环境的温度(环境温度)。
可以合理地推断出,被加热物体的温度与环境温度之间的差值越大。物体的冷却率就越高。




判断模型是否合理


e.g.2 Drug by injection 注射 / intravenous infusion 静脉注射
f两种注射方式分别对应最初讨论的两种“指数变化模型变体”


药物吸收的最简单模型基于以下假设
任何时候药物浓度的下降率都与当时的浓度成正比。
让我们考虑两种情况:
情况 1. 通过注射给药。
情况 2. 通过静脉注射将药物持续输入血液输注

重点
Case2:持续注射


e.g.3 分段注射
举例说明。病人血液中的药物浓度在首次注射后 30 分钟内降至初始值的一半。
任何时候药物浓度的下降速度都与浓度成正比(成正比是指y=kx)的关系
假设 4 小时后再注射一次。求首次注射 5 小时后的药物浓度

利用衰减是指数,如上面所说,可以利用相同时间内变化的比例不变这一点

下面一个例题再次说明这一点

如何判断函数是否为指数衰减模型:
人话-化简后是不是指数函数

Bounded Growth Models
在更现实的模型中,在有利环境中增长的种群最初可以按照指数增长定律增长。• 然而,人口增长不会无限期地持续下去


Logistic Model 广义线性回归模型
之前的K是固定的,此时的K是与P有关的k = r(M-P),图像为一次函数。而P又和t有关。


Harvesting Model 收获模型
其实就是有外界因素对环境有持续影响

r、M、H都是正的常数,在logistic模型的基础上再减一个H,代表外界对系统的一个影响率
为方便我们分析该模型人数和时间的关系。将模型写成一个二次方程的形式,利用通解公式写出两个解的表达式,注意该方程的解即为PT图像的平衡点。

根据不同的H取值有平衡点的情况有3种
有两个平衡点的情况:即原方程有两个不同的正解

有一个平衡点,原方程只有一个大于0的解

无平衡点,原方程无解。外界对系统影响过大导致物种灭绝



例题:

先将模型的表达式化为二次方程(错因没写右边的=0,你是要求解,光写个左边的方程有啥用呢)






First order linear ODEs with constant coefficients 一阶线性常系数微分方程
一阶自治微分方程是一阶线性常系数的齐次形式,所以齐次通解是一样的
eg:



在air conditioner没打开的时间段0-10,即Newton's law的模型,是一阶自治微分方程(一阶线性齐次常系数方程)

在air conditioner打开的时间段10- 20,air condition对温度的改变是关于自变量t的函数,所以不再是一阶自治微分方程,而是一阶线性非齐次常系数方程
求非齐次一阶线性微分方程的步骤:
1.求齐次形式的通解
2.根据方程设特解,代回原式(非齐次),通过将相同参数的放在一起,求解特解中的系数。
最后将题目要求的自变量代入





Modeling periodic behaviour using ODEs


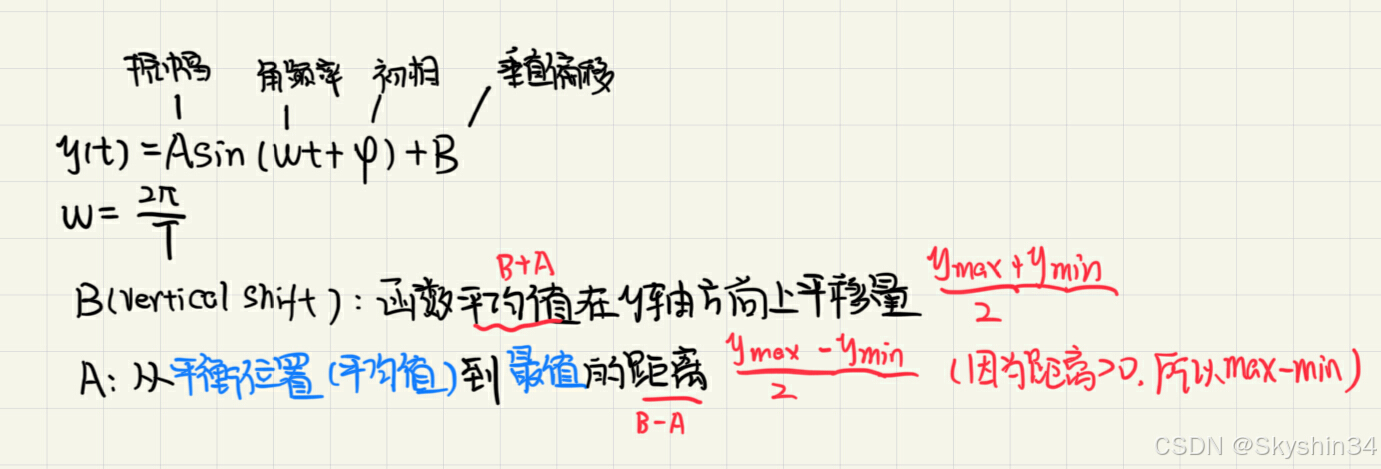



例2:
例3:



用欧拉法解常系数微分方程

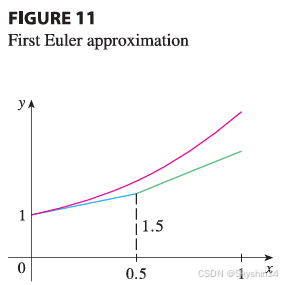





可以想象当h很短的时候,函数值即为这个区域的面积,三角形也可近似为矩形
使用不同步长的欧拉近似来逼近一个微分方程的解。步长减小到 0.25,这样得到的近似解更接近真实解。这表明减小步长可以提高欧拉方法的近似精度。


PDE定义:偏微分方程(Partial Differential Equation)
Reference:












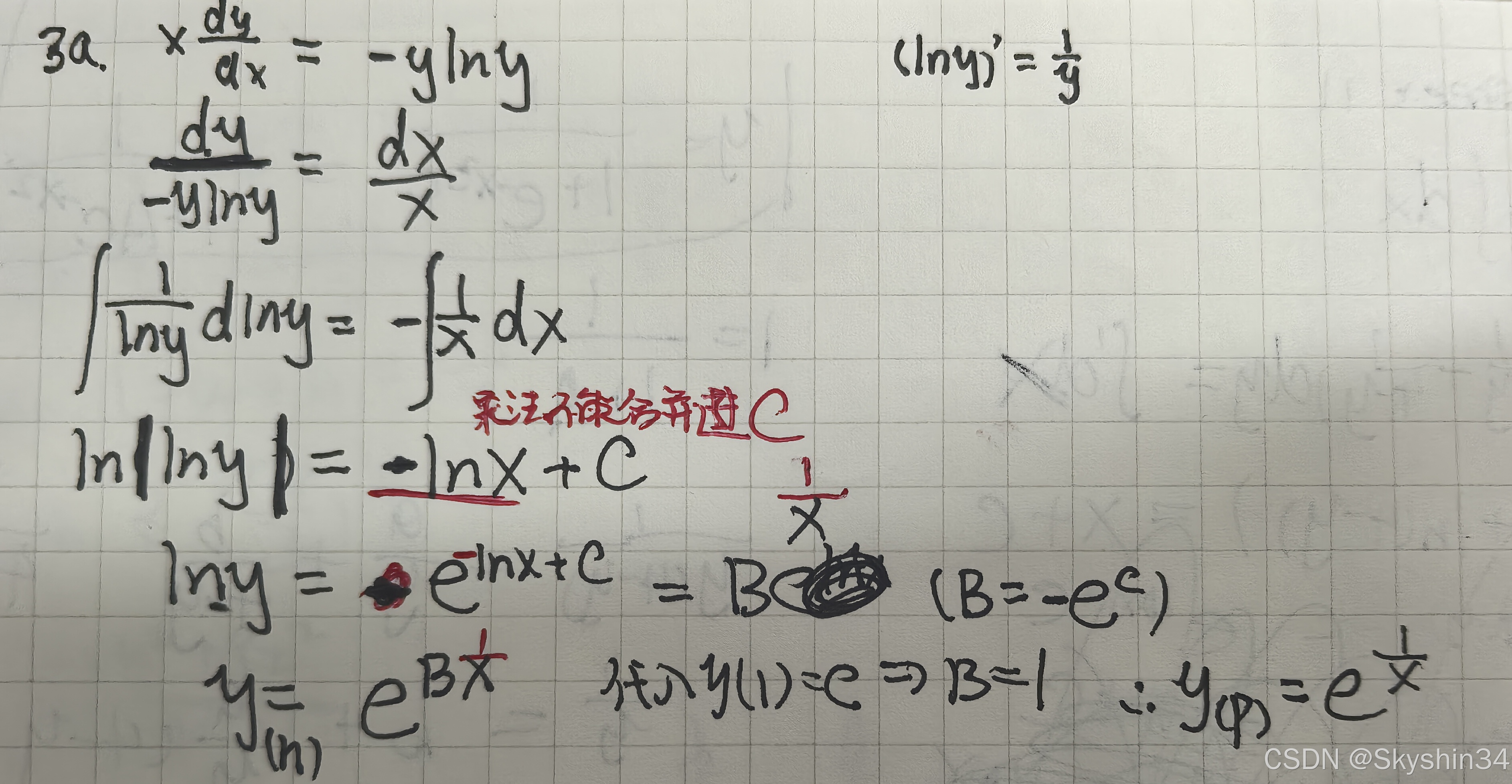








































 124
124

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








