基于结构相似性的垃圾邮件聚类

基于结构相似性的垃圾邮件快速有效聚类

1 引言

垃圾邮件是一个臭名昭著且长期存在的问题，远未得到解决。去年，全球平均每天发送的1914亿封电子邮件中[20]，超过70%为垃圾邮件。垃圾邮件引发了许多问题，从直接的经济损失，到互联网流量、存储空间和计算资源的滥用[22]。此外，垃圾邮件正逐渐成为实施各种网络犯罪的工具，例如网络钓鱼、恶意软件分发或基于社会工程学的诈骗。

鉴于该问题的相关性，已有多种方法被提出以应对垃圾邮件问题。目前，用于对抗垃圾邮件的最常用方法是通过过滤器在接收方设备上识别并拦截这些邮件，这些过滤器通常基于机器学习技术或内容特征，例如关键词或非ASCII字符[5,8,25]。

不幸的是，这些防御措施仅能略微缓解问题，而该问题仍然给用户和公司带来不可忽视的成本。为了有效应对垃圾邮件问题，必须找到并追查那些通常隐藏在复杂受感染设备网络背后的垃圾邮件发送者，这些设备违背用户意愿发送垃圾邮件，即僵尸网络。因此，应通过分析电子邮件的文本、附件及其他元素（如链接）来推断有助于发现垃圾邮件发送者的信息。因此，对相关垃圾邮件进行早期分析至关重要[2,7]。然而，由于垃圾邮件数量巨大且每小时持续大幅增长（每小时80亿封）[20]，以及由于使用混淆技术导致相关邮件本身具有高度方差[19]，此类分析任务极具挑战性。为了简化这一分析过程，通常通过蜜罐收集的大量垃圾邮件应被划分为不同的垃圾邮件活动[29]。垃圾邮件活动是指垃圾邮件发送者为实现特定目的（如广告产品、传播思想或出于犯罪意图）而传播的一组消息[6]。

本文提出了一种基于结构相似性快速且有效地对大量垃圾邮件进行分组的方法论。通过考虑一组21个区分性结构特征，获得同质邮件组，以识别不同的垃圾邮件活动。基于电子邮件的相似性对其进行分组是一种已知的方法。然而，先前的研究主要集中在少数特定参数的分析上[2,21,29,30]，其结果的准确率仍然在某种程度上受限。本文提出的方案基于一种名为分类层次聚类的算法，该算法称为分类聚类树（CCTree），在[27]中提出，构建一棵叶节点代表各种垃圾邮件活动的树。该算法通过结构相似性对电子邮件进行聚类（分组），并在每一步验证所获得聚类的同质性，将不够同质（纯）的组根据产生最大方差（熵）的属性进行划分。所提出方法的有效性已在从真实近期数据集提取的1万封垃圾邮件[1]上进行了测试，并与其他知名的类别型聚类算法进行了比较，在聚类质量（即纯度和准确率）和时间性能方面均取得了最佳结果。

本文的贡献可以总结如下：
- 我们提出了一种基于分类聚类树（CCTree）算法的框架，用于有效且高效地分析和将大量原始垃圾邮件聚类为垃圾邮件活动。
- 我们引入了一组代表邮件结构的21个类别型特征，并简要讨论了数值特征的离散化过程。
- CCTree的性能已通过内部评估进行了全面评估，以估计其生成同质聚类的能力，以及通过外部评估来评估其在已知类别的情况下有效分类相似元素（电子邮件）的能力。内部评估和外部评估分别在一个包含10k条未分类垃圾邮件的数据集和一个包含276封人工分类电子邮件的数据集上进行。

• 我们提出并通过在20万封垃圾邮件上的分析验证了一种方法论，该方法论基于同质性-簇数量图上的最大曲率点（拐点）检测，以选择最优的CCTree配置参数。
• 我们将提出的方法与两种通用的类别聚类算法以及其他针对垃圾邮件聚类的特定方法进行了比较。

本文的其余部分结构如下。第2节报告了分类聚类树（CCTree）算法的形式化描述和理论背景。第3节描述了所提出的框架，详细说明了提取的特征并报告了实现细节。第4节报告了用于评估CCTree在垃圾邮件聚类方面能力的实验，并将其结果与两种著名的类别聚类算法的结果进行了比较。同时报告并验证了设置CCTree参数的方法论。第5节讨论了所提出方法的局限性和优势，并与一些相关工作进行了结果比较。关于垃圾邮件聚类的其他相关工作在第6节中介绍。最后，第7节简要总结并提出了未来研究方向。

2 分类聚类树

2.1 CCTree 构建

CCTree通过类似决策树的结构迭代构建，树的叶节点即为期望的聚类。图1中展示了CCTree的一个示例。CCTree的根节点包含所有待聚类的元素。每个元素通过一组类别型属性进行描述，例如消息的语言。由于是类别型属性，每个属性只能取有限个离散值，这些值构成其域。例如属性语言的域可以是：{英语、法语、西班牙语}。在每一步中，若前一层的节点同质性不足，则将其分裂，生成树的新一层。香农熵[26]被用于定义一种称为节点纯度的同质性度量，并用于选择分裂节点所使用的属性。具体而言，非叶节点根据能产生最大香农熵值的属性进行划分。这种划分通过对应于特定属性各个可能结果的分支来表示。从父节点引出的每个分支或边都标记有选定的特征，该特征将数据导向子节点。CCTree构建过程可形式化如下。

输入 ：设 D为一组数据点，包含在属性集 A上的 N个元组，共有 d个属性，并设 S为一组停止条件。

属性 ：给定一个包含 d个属性的有序集合 A={A1, A2,…, Ad}，其中每个属性是一个互斥值的有序集合。因此，第 j个属性可表示为 Aj={v1j, v2j,…, v(rj)j}，其中 rj是属性 Aj的特征数量。

数据点 ：给定一组 D，包含 N 个数据点，其中每个数据点是一个向量，其元素为属性的特征。

停止条件 ：给定一组停止条件 S=({μ, ε})。 μ 是“节点中元素的最小数量”，即当节点中的元素数量少于 μ 时，即使节点纯度不够高，也不再进行划分。 ε 表示每个簇的“期望的最小纯度”，即当节点的纯度达到或优于 ε 时，该节点将被视为叶节点。为了计算节点纯度，定义了一个基于香农熵的函数如下：

设 Nkji 表示在节点 i中具有第 j个属性的第 k个值的元素数量。令 Ni为节点 i中的元素数量。因此，考虑 p(vkji) = Nkji / Ni ，节点 i的纯度，记为 ρ(i)，定义如下：

ρ(i) = −∑ {j=1}^{d} ∑ {k=1}^{rj} p(vkji) log(p(vkji))

其中 d为属性数量， rj为第 j个属性的特征数量。

输出 ：CCTree算法的最终输出是由CCTree的叶节点构成的簇集合。有关 CCTree算法的更多详细信息，我们建议读者参考[27]。

3 框架

所提出的框架分为两个步骤进行。首先，通过解析器对原始邮件进行分析，以提取结构特征向量。随后，利用引入的CCTree算法对收集的向量（元素）进行聚类。本节报告了有关分析与聚类垃圾邮件的所提出框架及提取的特征的详细信息。

3.1 特征提取与定义

为了描述垃圾邮件，我们选择了一组21个类别型属性，这些属性代表了电子邮件的结构属性。原因是属于同一垃圾邮件活动的消息通常在整体外观上基本保持不变，尽管垃圾邮件发送者通常会插入随机文本或链接[6]。所选属性扩展了[18]中提出的用于将电子邮件标记为垃圾邮件或非垃圾邮件的结构特征集。表 1列出了这些属性及其简要描述。

属性	描述
收件人数量	收件人地址的数量。
NumberOfLinks	邮件文本中的总链接数。
NumberOfIPBasedLinks	显示为IP地址的链接数。
NumberOfMismatchingLinks	文本与实际链接不同的链接数。
链接中域名数量	链接中的域名数量。
每条链接平均点数	文本中链接的平均点数。
包含“@”的链接数量	包含“@”的链接数量。
包含十六进制字符的链接数量	包含十六进制字符的链接数量。
主题语言	主题的语言。
含非ASCII字符的链接数量	含有非ASCII字符的链接数量。
是否为HTML	如果邮件包含HTML标签，则为True。
邮件大小	电子邮件的大小，包括附件。
语言	电子邮件的语言。
附件数量	附件的数量。
附件总大小	电子邮件附件的总大小。
最大附件的文件类型	最大附件的文件类型。
主题中的字数	主题中的字数。
主题中的字符数	主题中的字符数。
主题中包含“Re”或“Fwd”	如果主题中包含“Re”或“Fwd”，则为真。
主题中的非ASCII字符数	主题中非ASCII字符的数量。
电子邮件文本中的图片数量	电子邮件文本中的图像数量。

由于聚类算法是类别型的，因此所有选定的特征也都是类别型的。值得注意的是，某些特征原本用于表示数值型值，例如附件总大小，而非类别型特征。然而，我们总可以通过定义区间并将每个区间分配一个特征值，将这些特征从数值型转换为类别型。我们基于Chimerge离散化方法[15]来选择这些区间，该方法在决策树类问题的离散化中表现出色[10]。

3.2 实现细节

在实现方面，已使用Java开发了一款电子邮件解析器，用于自动分析原始邮件文本并以向量形式提取特征。该软件利用JSoup[14]进行HTML解析，并利用 LID1 Python工具进行语言识别。LID软件采用n‐gram技术来识别文本的语言。

对于LID需要识别的每种语言，必须向软件提供相应的词库，以便提取 n‐gram。LID所训练的语言包括：英语、意大利语、法语、德语、西班牙语、葡萄牙语、中文、日语、波斯语、阿拉伯语、克罗地亚语。

我们使用MATLAB2软件实现了CCTree算法，该算法以解析器提取的电子邮件特征矩阵作为输入。

值得注意的是，完整的框架，即特征提取和聚类模块，完全可以在不同的操作系统上移植。事实上，特征提取模块和聚类模块（即MATLAB）都是基于 Java的，可在绝大多数通用操作系统（Java、 UNIX、 iOS等）上运行。此外，用于语言分析的Python模块也具有可移植性。而且，LID被设计为一个可选组件，即如果缺少Python解释器，分析也不会中断。对于无法推断语言的电子邮件，将使用UKNOWNLANGUAGE作为该属性的值。

4 评估与结果

本节报告了用于评估CCTree算法在垃圾邮件聚类问题上性能的实验结果。首先，在一个包含10,000封近期垃圾邮件的数据集上（二月 2015[1]的第一周）进行了一组实验，以评估CCTree算法生成同质聚类的能力。这种评估称为内部评估，用于衡量聚类算法的质量，通过计算每个簇内元素之间的相似性以及与其他簇元素的相异性来评估聚类结果的质量。第二组实验旨在评估CCTree使用已知基准类别的小型数据集正确分类数据的能力。该评估被称为外部评估，用于衡量特定算法生成的聚类结果与预分类数据集中期望的聚类（类别）之间的相似性。

在外部评估中，CCTree在一个由276封电子邮件组成的数据集上进行了测试，这些电子邮件被手动标注为29个类别3。这些电子邮件的划分同时考虑了消息的结构和语义。因此，属于同一类别的电子邮件可被视为同一垃圾邮件活动的一部分。CCTree的结果与两种类别型聚类算法，即COBWEB和CLOPE。选择COBWEB和CLOPE是因为它们分别以高准确性和极快速度而著称。在前述相同的数据集上，对内部评估和外部评估均进行了比较。同时，还报告了时间性能分析。值得注意的是，这三种算法均基于Java工具实现，因此时间比较具有有效性。

COBWEB[9]是一种类别型聚类算法，它构建一个树状图，其中每个节点都关联一个条件概率，用于概括属于特定节点的对象的属性值分布。与 CCTree算法不同，COBWEB还包含合并操作，可将两个独立的节点合并为一个节点。COBWEB在计算上开销较大且耗时，因为它在每一步都会重新分析每一个数据点。然而，由于其较高的准确率，COBWEB算法被广泛应用于多个领域，其被称为类别效用的相似性距离度量也被用于评估分类聚类的准确率[3]。实验中使用了WEKA[12]中实现的COBWEB。

CLOPE[32]是一种快速的类别型聚类算法，旨在最大化具有相同属性值的元素数量，以提高每个获得簇的同质性。对于CLOPE，我们在实验中使用了 WEKA的实现。

4.1 内部评估

内部评估用于衡量聚类算法获得同质聚类的能力。在内部评估中得分较高的聚类算法能够最大化簇内相似性（即同一簇内的元素相似），并最小化簇间相似性（即不同簇的元素不相似）。簇之间的相异性通过计算各个簇中元素（数据点）之间的距离来度量。所使用的距离函数随具体问题而变化。特别是对于由分类属性描述的元素，无法使用常见的几何距离（如欧几里得距离）。因此，在本研究中采用汉明和雅可比距离度量[13]。内部评估可直接在聚类算法所操作的数据集上进行，即无需事先知道类别（期望的聚类）。内部评估指标包括邓恩指数[4]和轮廓系数[23]，定义如下：

邓恩指数 。设 Δi为簇 Ci的直径，可定义为 Ci中元素的最大距离：Δi= max{x,y∈Ci, x≠y}{ d(x, y)}，其中d(x, y)度量了元素对 x和 y之间的距离， |C|表示属于簇 C的元素数量。同时，设 δ(Ci, Cj)为簇 Ci和 Cj之间的簇间距离，该距离通过两个簇中元素之间的成对距离计算得到。那么，在 k个聚类组成的集合上，邓恩指数[11]定义为：

DIk= min_{1≤i≤k}{min_{1≤j≤k}{ δ(Ci ,Cj) / max_{1 ≤ t ≤ k} Δt }}

较高的邓恩指数值意味着更好的聚类质量。值得注意的是，邓恩指数的值会受到最大直径的负面影响。

轮廓系数 。令 d(xi)表示数据点 xi与其所在同一簇内的其他数据点之间的平均相异度。同时，令 d′(xi)表示 xi到任何其他簇（不包括 xi所属的簇）的最低平均相异度。那么，数据点 xi的轮廓系数 s(i)定义为：

s(i)= (d′(i)− d(i)) / max{d(i), d′(i)} =
⎧
⎪⎨
⎪⎩
1 − d(i)/d′(i) if d(i)< d′(i)
0 if d(i)= d′(i)
d′(i)/d(i) −1 if d(i)> d′(i)

其中定义结果为 s(i) ∈[−1, 1]。 s(i)越接近1，表示数据点 xi的聚类越合适。一个簇中所有数据的 s(i)的平均值反映了簇内数据的紧密程度。因此， s(i)的平均值越接近1，聚类结果越好。为了便于解释，所有已聚类点的轮廓系数也通过轮廓图进行展示。

性能比较 。如第2节所述，CCTree算法需要两个停止条件作为输入，即节点中最少元素数量（μ）和簇的最小纯度（ε）。此后，符号CCTree(ε, μ)将用于表示 CCTree算法的具体实现。

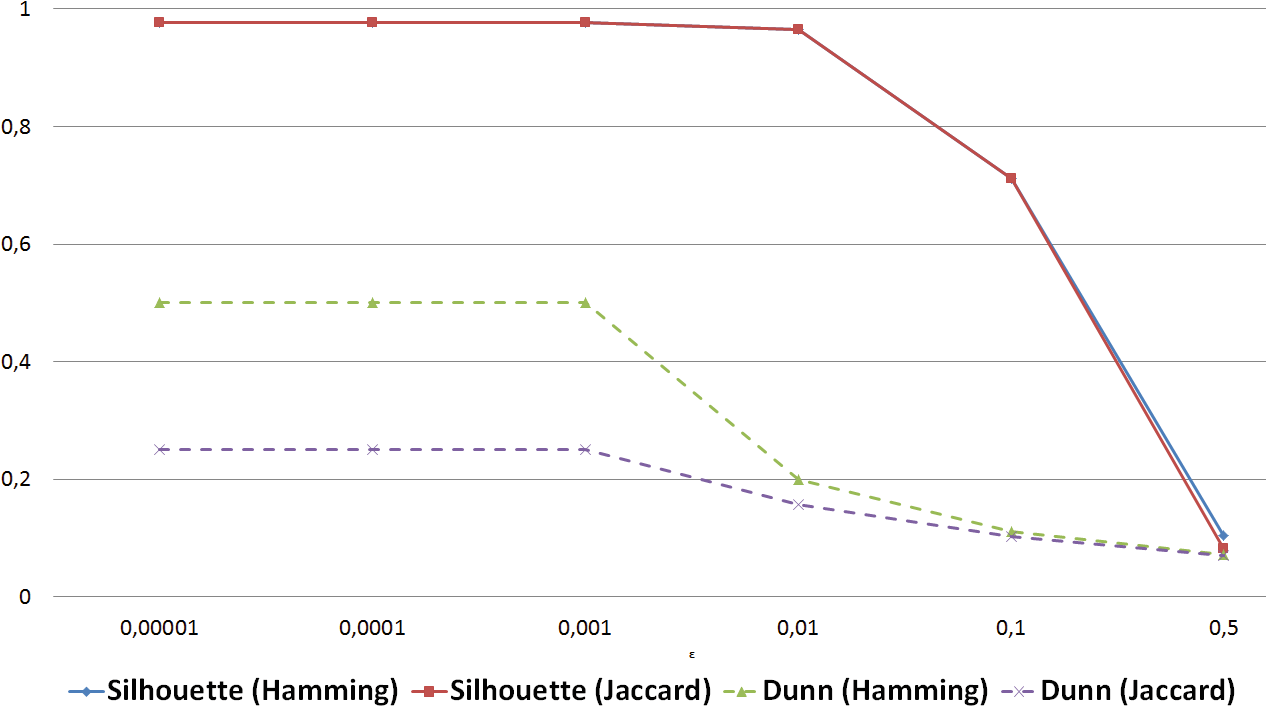
图2展示了当最小元素数量 μ设为1时，CCTree在五种不同 ε值下的内部评估指标。值得注意的是，如果 μ= 1，唯一影响结果的停止条件就是节点纯度。因此，我们首先固定 μ= 1，以找出该数据集所需的最优节点纯度。

如图2所示，当ε= 0.001时，纯度值达到最大并稳定。更严格的纯度要求（即 ε< 0.001）不会进一步提高精度。该 ε值将在后续评估中保持不变。

固定节点纯度 ε= 0.001，我们寻找更合适的 μ参数值，以便能够将 CCTree的性能与精确的COBWEB和快速的CLOPE进行比较。为此，我们提供了簇中最小元素数量的四个不同取值。表2展示了针对 μ所提数值（即1、10、100和1000）的轮廓系数和邓恩指数结果。此外，表2最后两行报告了生成的聚类数量以及生成聚类所需的时间。表2还报告了与前述两种类别型聚类算法 COBWEB和CLOPE的比较结果。从左起前两列显示了在轮廓指数方面的聚类精度具有可比性的结果。事实上，当CCTree的纯度设置为 ε= 0.001且最小元素数量设置为 μ= 1时（CCTree(0.001,1)），COBWEB和CCTree都表现出良好的精度。对于两种距离度量方式，COBWEB在轮廓指数上表现略优。然而，这种差异（小于2%）可以忽略不计，因为COBWEB生成的聚类数量几乎是 CCTree(0.001,1)的两倍。可以推断，更多数量的小型聚类会提高内部同质性（例如，单个元素的聚类是完全同质的）。但正如接下来将详细说明的那样，聚类数量远大于预期组数是不可取的。此外，CCTree(0.001,1)在邓恩指数上的表现优于COBWEB。需要指出的是，邓恩指数的值受最差结果聚类的聚类同质性影响较大。CCTree(0.001,1)返回的值表明，与COBWEB相比，所有返回的聚类整体上具有更好的同质性，即CCTree(0.001,1)的最差聚类比 COBWEB的最差聚类要同质得多。表2最右列报告了CLOPE聚类算法的结果。CLOPE是一种类别型聚类算法，以其快速生成尽可能纯的聚类而闻名。CLOPE在轮廓系数上的准确率相当有限，在邓恩指数上则为零。

算法	COBWEB	CCTree - ε= 0.001	CCTree - ε= 0.001	CCTree - ε= 0.001	CCTree - ε= 0.001	CLOPE
算法	µ= 1	µ= 10	µ= 100	µ= 1000
轮廓系数 (汉明)	0.9922	0.9772	0.9264	0.7934	0.5931	0.2801
轮廓系数 (杰卡德)	0.9922	0.9777	0.9290	0.8021	0.6074	0.2791
Dunn (汉明)	0.1429	0.5	0.1	0.0769	0.0769	0
Dunn (杰卡德)	0.1327	0.25	0.1	0.0879	0.0857	0
聚类	1118	619	392	154	59	55
时间（秒）	17.81	0.6027	0.3887	0.1760	0.08610	3.02

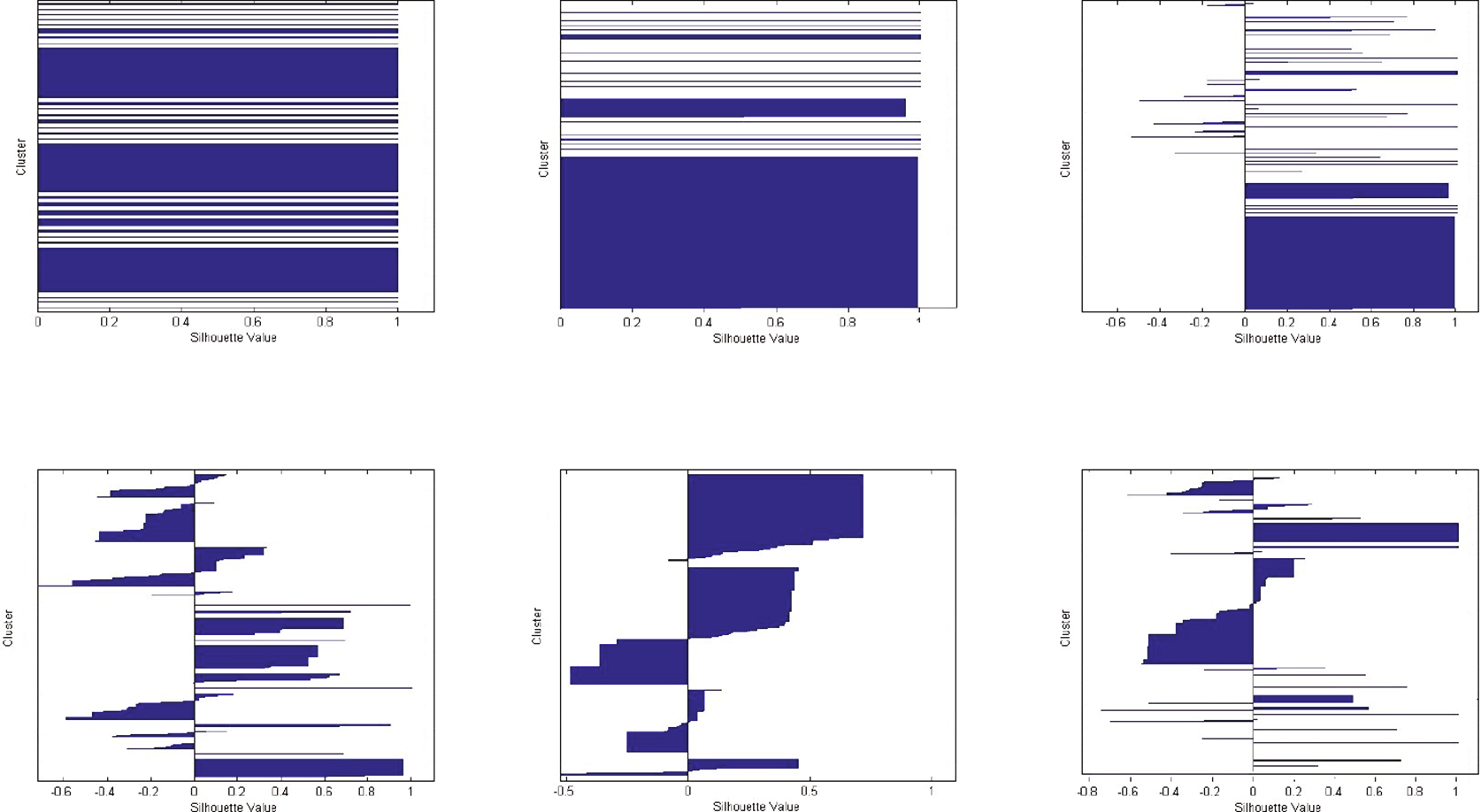
表2中聚类准确率差异的图形化描述可从图3的汉明轮廓图中推断得出。这些图是水平直方图，其中每个条形代表每个数据点s(i) ∈[−1, 1]的轮廓系数结果 xi，依据前述定义。两者均 COBWEB 和 CCTree(0.001,1)未出现负值，大多数数据点的得分为 s(i)= 1。事实上，对于CCTree(0.001, 1000)，最差的数据点得分不低于 −0.5，而 CLOPE的一些数据点轮廓系数为 −0.8，这将导致其聚类中存在严重的非同质性。此外，具有正值的数据点数量在CCTree(0.001,1000)中远多于CLOPE。

最后，表2还报告了各算法执行聚类所消耗的时间。可以看出，COBWEB以准确率为代价，在包含1万封电子邮件的数据集上耗时17秒，而速度更快但准确率低得多的CLOPE仅耗时3秒。CCTree算法优于COBWEB和CLOPE，在最精确的配置（CCTree(0.001,1)）下仅需0.6秒。从内部评估结果可以得出结论： CCTree算法获得的聚类质量与COBWEB相当，且所需计算时间甚至少于快速但不准确的算法CLOPE。

4.2 CCTree参数选择

通过内部评估以及表2和3中报告的结果，我们展示了内部评估指标和聚类数量对 μ和 ε参数值的依赖性。接下来我们将简要讨论一些正确选择CCTree参数以最大化聚类效果的指南。

关于 ε参数，我们在第4节中表明，可以通过设置 ε并调整 μ= 1来改变 ε，从而在准确率上找到固定点，即认为最优的 ε是当进一步减少 ε不再提升准确率时的取值。

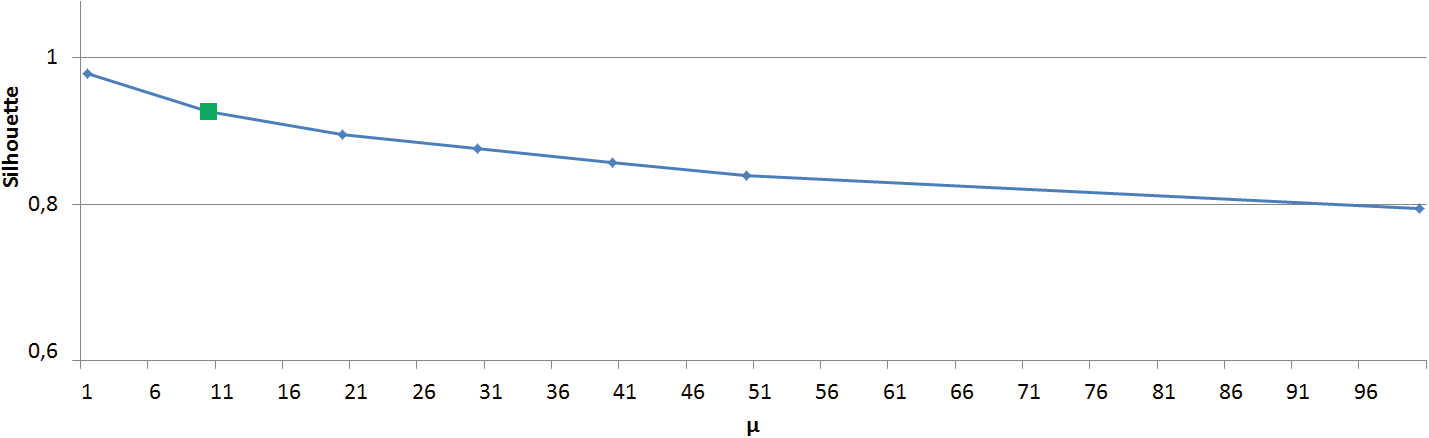
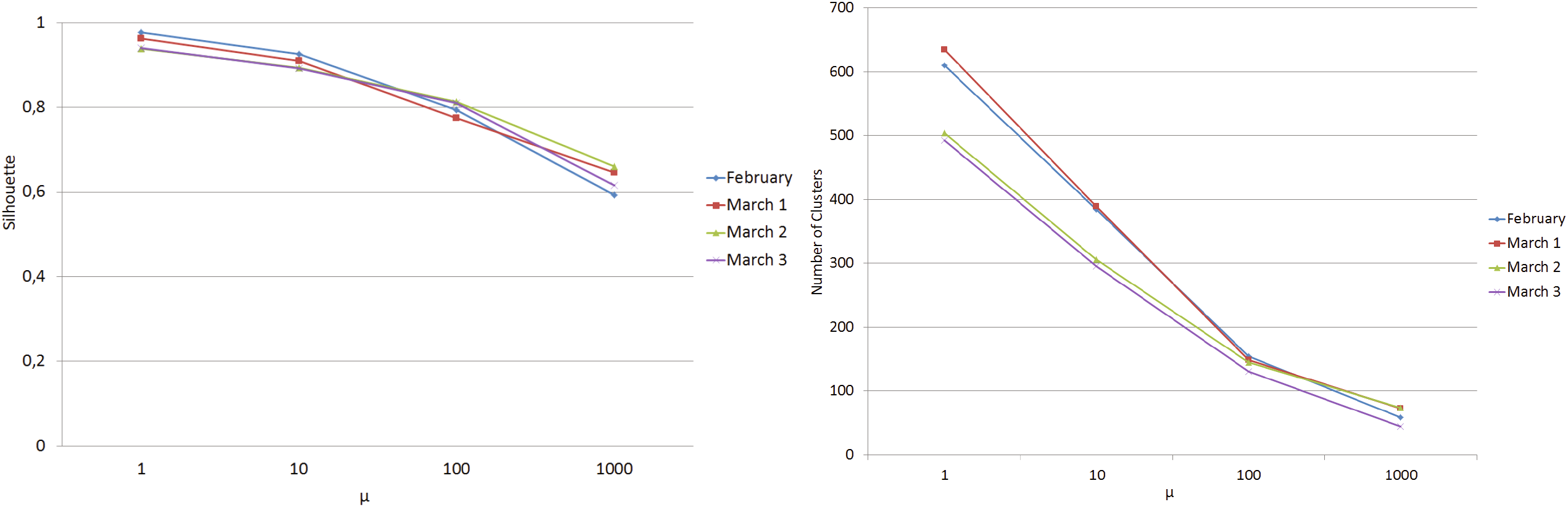
固定参数 ε，必须选择参数 μ以在准确率和生成的聚类数量之间取得平衡。由于聚类数量是受 μ参数影响，可以通过已知的最优簇数来选择 μ的最优值。层次聚类算法的最优簇数估计问题已在[24]中通过确定簇间距离随聚类数量变化曲线上的最大曲率点（拐点）得以解决。考虑到轮廓指数与簇间距离成反比关系，因此在图 4所示的基于内部评估所用数据集、采用七种不同 μ值计算得到的轮廓系数（汉明）图上寻找拐点是合理的。该图报告了在相同内部评估数据集上计算的结果。为了便于表示，本图未显示 μ大于100时的曲线。应用文献[24]中描述的L‐方法，可以发现拐点位于 μ= 10。进一步的分析可从表3和图5的结果中得出，它们展示了来自2015年3月三个不同周的垃圾邮件蜜罐[1]中的三个额外垃圾邮件数据集的分析结果。这些数据集的规模与用于内部评估的数据集（2015年2月第一周）相近，分别包含10k、10k和9k封垃圾邮件。从表格和图形中均可看出，所有测试数据集在轮廓值和聚类数量上的趋势保持一致。因此我们验证了：(i) 拐点方法论的有效性；(ii) 对于相同类型且规模相近的数据集，可以使用相同的 CCTree参数。

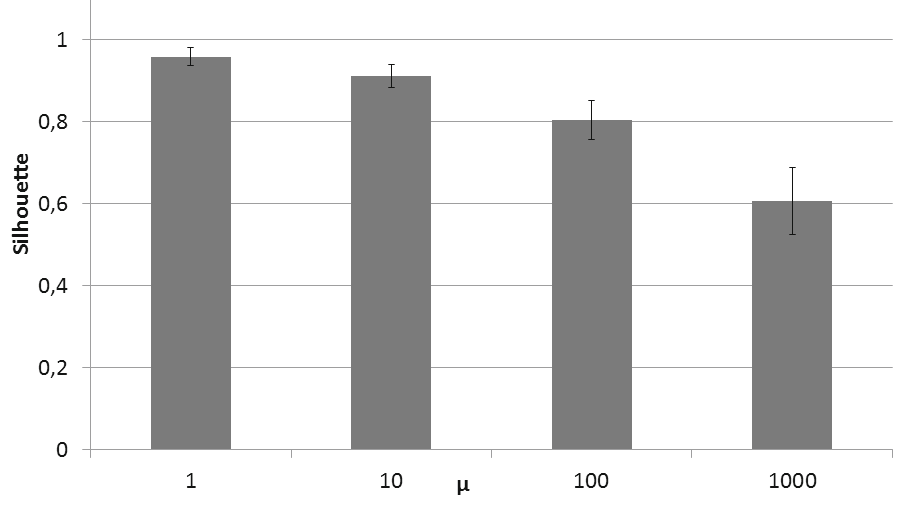
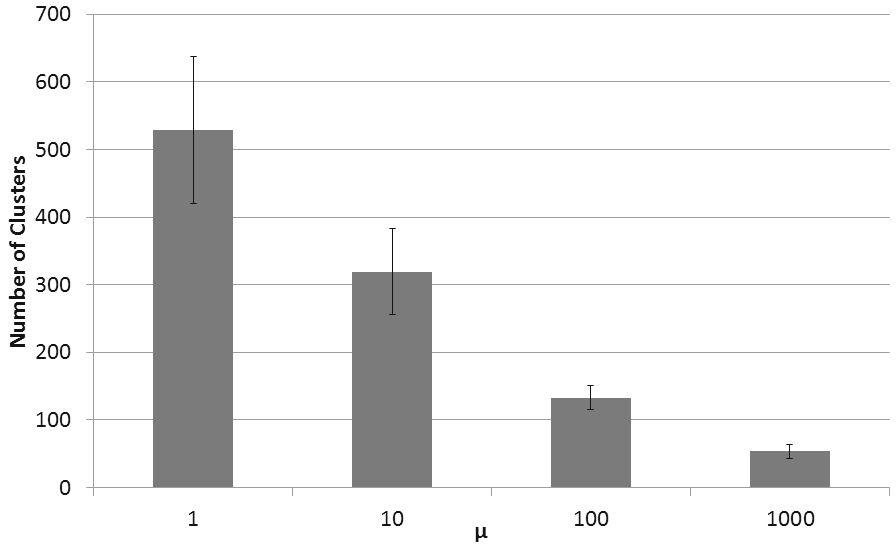
为了对参数确定性分析提供统计有效性，我们分析了一个包含2014年10月至2015年5月从[1]蜜罐收集的超过20万封电子邮件的数据集。这些电子邮件被分为20个数据集，每个数据集包含1万封垃圾邮件。每个数据集代表一周垃圾邮件。图5显示了在20个数据集上计算的聚类数量和轮廓系数平均值，这些值随着先前实验中设定的 μ参数（即1、10、100、1k）的变化而变化。标准差也以误差条形式标出。值得注意的是， μ={1, 10}在20个数据集上的标准差略高于2%，而对于 μ= 100则达到4%，对于 μ= 1000则达到8%，这与表3的结果一致。在聚类数量方面也获得了类似的结果，其中标准差的最大值如预期一样出现在 μ= 1，高达108，这也与表3的结果一致。因此，对于所有分析的20个数据集（涵盖八个月的垃圾邮件），我们总能在 μ= 10时找到轮廓系数和聚类数量的拐点（图6）。

Data	轮廓系数	聚类	轮廓系数	聚类	轮廓系数	聚类	轮廓系数	聚类
Data	μ= 1	μ= 1	μ= 10	μ= 10	μ= 100	μ= 100	μ= 1000	μ= 1000
二月	0.9772	610	0.9264	385	0.7934	154	0.5931	59
三月 I	0.9629	635	0.9095	389	0.7752	149	0.6454	73
三月 II	0.9385	504	0.8941	306	0.8127	145	0.6608	74
三月 III 0.9397	493	0.8926	296	0.8102	131	0.6156	44

4.3 外部评估

外部评估是一种衡量聚类算法正确分类数据能力的标准技术。为此，会在一个类别（即期望的聚类）已知的小型数据集上进行外部评估。预先。用于外部评估的一个常见指标是F‐值[17]，它将正确分类元素和错误分类元素的性能合并为一个单一指标。

形式上，设集合{C1, C2,…, Ck}为数据集 D的期望聚类（类别），并设 {C1′, C2′,…, Cl′}为在 D上应用聚类算法所得到的簇集合。那么，每个簇 Ci的 F‐值 F(i)以及数据集上的全局F‐值 Fc定义如下：

F(i)= max_{i,j} \frac{|C_i ∩ C’_j|^2}{|C_i| \cdot |C’_j|}

Fc= \sum_{i=1}^{k} F(i) \frac{|C_i|}{| \cup_{j=1}^{k} C_j |}

F‐值的结果返回范围为[0,1]，其中1表示理想情况，即该簇 Ci恰好等于所得聚类中的一个。

Experimental Results . 为了进行外部评估，已手动分析并分类了从不同邮箱的垃圾邮件文件夹中收集的276封垃圾邮件。这些电子邮件根据原始邮件消息的结构相似性被划分为29个组（类别）。外部评估集与用于内部评估的集合没有交集。

算法 COBW	EB CCTree	- ε= 0.001	- ε= 0.001	- ε= 0.001	- ε= 0.001	CLOPE
算法 COBW	EB CCTree	µ= 1	µ= 5 0.6331 0	µ= 10 .6330 0.	µ= 50	CLOPE
F‐值 0.3582		0.62				0.0076
聚类	194	102	73	50	26	15

外部评估的结果如表4所示。在内部评估结果的基础上，节点纯度的值被设置为 ε= 0.001以获得同质聚类。以下是对 μ取值的合理性说明。 μ= 1表示一个CCTree实例化过程，其中 μ参数不影响结果。另一方面 μ= 50返回的聚类数量与手动收集的29个聚类相当。对于此规模的数据集，更高的μ值不会改变结果。最佳结果出现在 μ={5, 10}时。这两个值的F‐值高于0.63，差异可以忽略不计，即使生成的聚类数量高于预期数量。

表4还报告了与COBWEB和CLOPE算法的比较。结果表明，CCTree算法在F‐值指标上优于COBWEB和CLOPE，显示出其在正确分类垃圾邮件方面具有更强的能力。我们回顾一下，在内部评估中，COBWEB的结果略优于 CCTree。这种差异的原因在于生成的聚类数量。事实上，COBWEB总是返回较多的簇（表4）。这通常会产生较高的聚类同质性（多个小型且同质的聚类）。然而，这并不一定意味着具有良好的分类能力。事实上，如表4所示，COBWEB 在包含 276 封电子邮件的数据集上生成了近 200 个聚类，是预期聚类数量（即 29 个聚类）的六倍。这导致了 COBWEB 算法较低的F值分数。值得注意的是，即使不考虑每个节点的最小元素数量（即μ= 1）， CCTree 的表现仍优于 COBWEB。另一方面，CLOPE 在 276 封电子邮件的数据集上在F值上的表现也较差。实际上，CLOPE 算法仅生成了 15 个聚类，少于预期聚类数量的一半，其F‐值分数为 0.0076。

5 讨论与比较

结合对21个特征的分析，提出的方法能够适用于分析几乎任何类型的垃圾邮件。这是相较于其他方法的主要优势之一，因为其他方法主要利用一两个特征将垃圾邮件聚类为活动。这些特征分别是链接[2,16]，关键词[5,8,25]，或图像[33]，且通常单独使用。这些方法论的分析仅局限于确实包含相应特征的垃圾邮件。然而，不含链接和/或图像的电子邮件在垃圾邮件中占有相当大的比例。事实上，从用于内部评估的数据集分析来看，在10165封电子邮件中，有4561封不包含任何链接。此外，仅有810封电子邮件包含图像。为了验证这些方法的聚类能力，我们实现了三个程序，基于内部评估数据集中电子邮件所包含的URLs、报告的域名以及远程图像链接进行聚类。不含链接和图片的电子邮件未被纳入考虑。

表5列出了每种方法生成的聚类数量。值得注意的是，在大规模数据集上，这些聚类方法高度不准确，生成的活动数量接近于分析元素的数量，因此，几乎每个簇都只包含单个元素。作为对比，我们列出了CCTree和COBWEB最精确实现的结果，这两种方法能够产生极度同质的聚类，并报告了99%的轮廓系数值。我们指出，由于不同组的使用特征存在差异，因此比较轮廓系数并无意义。我们还与基于FPTree等其他方法进行了对比。

簇 方法论	分析的电子邮件 生成的活动
基于链接的聚类	4561 4449
基于域的聚类 4561	4547
基于图像的聚类	810 807
COBWEB (21个特征)	10165 1118
CCTree (0.001,10)	10165 392

6 相关工作

魏等人[31]提出了一种利用电子邮件主题成对比较的聚类方法。该提出的方法通过两种聚类算法引入了十一项特征来对垃圾邮件进行聚类。首先，使用凝聚层次聚类算法基于主题的成对比较对整个数据集进行聚类。随后，采用 connected componentgraph算法以提升性能。[29]的作者应用了一种基于k‐均值算法的方法论，称为O‐均值聚类，该方法利用从每封电子邮件中提取的十二项特征。O‐均值算法的前提是聚类数量事先已知，但这并不总是一个可行的假设。此外，作者使用了欧几里得距离，而对于他们所使用的多个特征而言，这种距离度量并不能提供有意义的信息。与此方法不同，CCTree采用了更通用的距离度量方式，即香农熵。此外，CCTree不需要将期望的聚类数量作为输入参数。[28]中讨论了该方法在基于目标的垃圾邮件分类问题中的应用。

频繁模式树（FP‐树）是另一种用于在大规模数据集中检测垃圾邮件活动的技术。[6,7]的作者从每封垃圾邮件中提取一组特征。FP‐树基于特征的频率构建。由于对邮件布局和URL特征的敏感表示，导致即使两封垃圾邮件仅有微小差异，也会被分配到不同的活动。因此，FP‐树方法容易受到文本混淆技术[19]的影响，这些技术被用来欺骗反垃圾邮件过滤器，以及动态生成的链接的电子邮件。我们的方法论基于不考虑文本和链接语义的分类特征，对这类欺骗更具鲁棒性。

7 结论与未来方向

本文提出了一种基于名为CCTree的类别型聚类算法的方法论，用于在垃圾邮件活动中对大量垃圾邮件进行聚类，并根据结构相似性对其进行分组。表示邮件结构的特征集已被精心选择，并通过离散化方法确定了每个特征的区间。CCTree算法已在两个垃圾邮件数据集上进行了广泛测试，以衡量其生成同质聚类的能力以及识别预定义垃圾邮件组的特异性。文中提供了选择CCTree参数的指南，同时在统计上证明了对于相同规模的相似数据集，所选参数具有确定性。鉴于已验证的准确率和效率，提出的方法可作为一种有价值的工具，帮助执法机构快速分析大量垃圾邮件，以发现并追查垃圾邮件发送者。

作为未来的工作，我们计划扩展提出的框架，以针对通过垃圾邮件发起的特定攻击。特别是我们认为，可以从CCTree结构中提取规则，用于识别与已知网络犯罪（如网络钓鱼或诈骗）相关的电子邮件。该框架将用于在大量真实的垃圾邮件中快速检测和分组与特定网络犯罪相关的垃圾邮件活动。