【强化学习】价值迭代

价值函数定义为

带入 R 的定义：

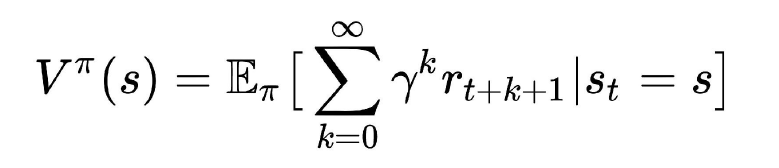
角标 $\pi$ 说明，所有状态的价值依赖于 agent 采取的策略。这是显然的，如果agent 永远不动，那么所有状态的价值都是 0，假设环境不会自己变化。

要求到最优的策略，先找最优的价值评估。

借助于价值函数的贝尔曼方程：

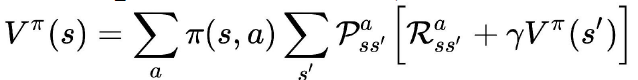
用迭代的方式求解出任意 策略$\pi$ 对应的价值函数。

最优的策略，就是每一步都选择价值最大的下一个状态。

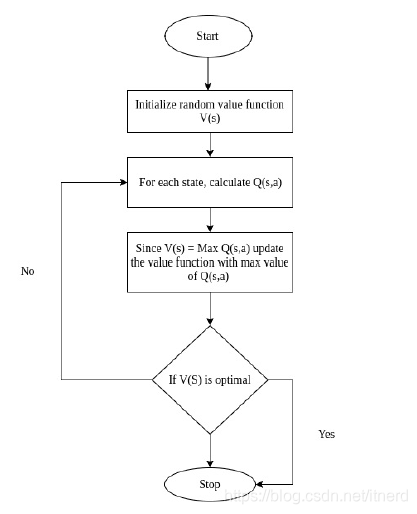
import gym
import numpy as np
env = gym.make('FrozenLake-v0')

def value_iteration(env, gamma = 1.0):
    value_table = np.zeros(env.observation_space.n) #随机初始化
    no_of_iterations = 10000 #最大迭代次数
    threshold = 1e-7 # 允许误差上限
    for i in range(no_of_iterations):
        updated_value_table = np.copy(value_table) #上一次迭代的价值函数
        for state in range(env.observation_space.n): #对每一个状态
            Q_value = [] # 记录每一个动作对应的 Q(s,a)，因为 V = max_a Q(s,a)
            for action in range(env.action_space.n):
                next_states_rewards = []
                for next_sr in env.P[state][action]: # 由于环境是随机的
                    trans_prob, next_state, reward_prob, _ = next_sr
                    next_states_rewards.append((trans_prob * (reward_prob + gamma *
                                                  updated_value_table[next_state])))
                Q_value.append(np.sum(next_states_rewards)) # 所有可能下一状态的价值的加权和
            value_table[state] = max(Q_value) # V = max_a Q(s,a)
        if (np.sum(np.fabs(updated_value_table - value_table)) <= threshold):
            print('Value-iteration converged at iteration# %d.' % (i + 1))
            break
    return value_table

def extract_policy(value_table, gamma = 1.0):
    policy = np.zeros(env.observation_space.n)
    for state in range(env.observation_space.n): # 对每一个状态
        Q_table = np.zeros(env.action_space.n)
        for action in range(env.action_space.n): # 对每一个动作
            for next_sr in env.P[state][action]:
                trans_prob, next_state, reward_prob, _ = next_sr
                Q_table[action] += (trans_prob * (reward_prob + gamma *
                                    value_table[next_state]))
        policy[state] = np.argmax(Q_table)
    return policy

optimal_value_function = value_iteration(env=env,gamma=1.0)
optimal_policy = extract_policy(optimal_value_function, gamma=1.0)
print(optimal_policy)