无信息搜索之迭代加深（iterative deepening）

The Rotation Game

描述
The rotation game uses a # shaped board, which can hold 24 pieces of square blocks (see Fig.1). The blocks are marked with symbols 1, 2 and 3, with exactly 8 pieces of each kind.

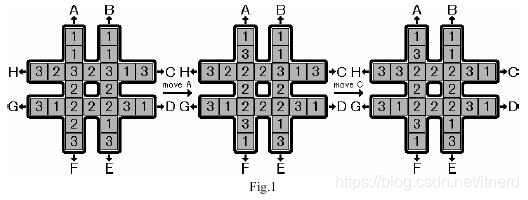
Initially, the blocks are placed on the board randomly. Your task is to move the blocks so that the eight blocks placed in the center square have the same symbol marked. There is only one type of valid move, which is to rotate one of the four lines, each consisting of seven blocks. That is, six blocks in the line are moved towards the head by one block and the head block is moved to the end of the line. The eight possible moves are marked with capital letters A to H. Figure 1 illustrates two consecutive moves, move A and move C from some initial configuration.

输入
The input consists of no more than 30 test cases. Each test case has only one line that contains 24 numbers, which are the symbols of the blocks in the initial configuration. The rows of blocks are listed from top to bottom. For each row the blocks are listed from left to right. The numbers are separated by spaces. For example, the first test case in the sample input corresponds to the initial configuration in Fig.1. There are no blank lines between cases. There is a line containing a single ‘0’ after the last test case that ends the input.

输出
For each test case, you must output two lines. The first line contains all the moves needed to reach the final configuration. Each move is a letter, ranging from ‘A’ to ‘H’, and there should not be any spaces between the letters in the line. If no moves are needed, output `No moves needed’ instead. In the second line, you must output the symbol of the blocks in the center square after these moves. If there are several possible solutions, you must output the one that uses the least number of moves. If there is still more than one possible solution, you must output the solution that is smallest in dictionary order for the letters of the moves. There is no need to output blank lines between cases.

样例输入

1 1 1 1 3 2 3 2 3 1 3 2 2 3 1 2 2 2 3 1 2 1 3 3
1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
3 1 1 2 1 1 1 3 2 2 1 1 2 2 2 2 3 3 3 3 2 3 3 1
1 3 3 3 1 1 2 2 1 1 1 2 2 3 3 3 2 2 2 1 1 3 2 3
1 3 1 3 2 2 3 3 1 1 3 2 1 3 3 2 1 2 1 3 1 2 2 2
2 3 1 3 3 2 1 3 3 1 1 2 1 3 2 3 2 1 2 1 3 2 1 2
1 2 2 3 2 1 3 3 1 1 3 1 3 3 2 3 2 1 1 1 2 2 3 2
1 2 2 2 1 3 3 3 1 3 2 1 1 1 3 2 3 2 3 1 2 1 3 2
2 2 3 2 1 3 1 3 1 3 2 3 1 1 3 2 2 2 3 1 3 1 1 2
3 2 1 2 1 3 1 3 3 3 2 2 1 1 3 3 2 2 3 1 1 1 2 2
1 2 2 2 1 3 3 3 3 3 2 1 1 3 1 2 3 3 2 2 1 1 1 2
1 3 1 1 2 3 2 2 2 1 3 3 2 2 3 1 1 3 1 2 2 3 1 3
1 3 1 1 2 1 3 2 2 1 3 2 2 2 3 3 1 3 1 2 1 3 2 3
1 2 2 2 3 2 1 1 3 2 1 1 3 2 3 3 1 3 1 2 2 3 3 1
3 2 1 2 2 1 2 2 1 1 3 3 3 2 3 1 1 3 1 2 3 3 2 1
3 2 2 1 3 2 3 1 2 3 1 1 1 2 2 2 1 3 3 1 3 1 3 2
3 1 2 2 3 2 3 1 2 3 1 1 1 1 2 2 2 2 3 3 3 1 3 1
3 2 3 1 3 2 3 1 2 3 1 2 1 2 2 1 2 3 3 1 2 1 3 1
3 1 3 2 1 2 1 1 3 2 3 2 3 1 2 2 1 2 1 3 2 3 3 1
3 3 3 1 1 2 3 1 1 2 3 1 2 1 2 2 2 3 3 3 1 1 2 2
0

样例输出

AC
2
DDHH
2
No moves needed
1
AHADDE
2
CACGAH
2
AAHEGACA
1
BDFFDHHFD
1
CBGFGBHHFD
1
ABGEECGAGAC
1
BBDFHBBHFG
2
AGAEHEEDHF
2
ABBCAACDE
1
ECGEGAACG
2
DBBFGHBHA
3
BDAEECGACB
3
BFHBDDFFHF
3
GEGHBFDBH
1
DDDBHBBFH
1
DADECCAEG
2
ADHAEECCG
2
DBDFCBFHHF
2

import java.util.Scanner;
import java.io.*;
//import java.util.Random;

/**
 *          A     B
 *          01    02
 *          03    04
 * H  05 06 07 08 09 10 11 C
 *          12    13
 * G  14 15 16 17 18 19 20 D
 *          21    22
 *          23    24
 *          F     E 
 *  
 *  input cases:
 * 1 1 1 1 3 2 3 2 3 1 3 2 2 3 1 2 2 2 3 1 2 1 3 3
 * 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3
 * 0
 */

public class Main {
	
	static class State{
		public String boardStr;
		public String lastOp;
		public State parent;
		public int depth;
		public State(State parent, String o, String s){
			State.this.parent = parent;
			State.this.lastOp = o;
			State.this.boardStr = s;
		}
		@Override
		public int hashCode(){
			return State.this.boardStr.hashCode();
		}
		public boolean check(){
			if(boardStr.charAt(6) == boardStr.charAt(7) &&
			   boardStr.charAt(7) == boardStr.charAt(8) &&
			   boardStr.charAt(8) == boardStr.charAt(11) &&
			   boardStr.charAt(11) == boardStr.charAt(12) &&
			   boardStr.charAt(12) == boardStr.charAt(15) &&
			   boardStr.charAt(15) == boardStr.charAt(16) &&
			   boardStr.charAt(16) == boardStr.charAt(17) )
				return true;
			return false;
		}
		public State move(String action){
			char[] board = boardStr.toCharArray();
			char temp;
			switch(action){
			case "A":
				temp = board[0];
				board[0] = board[2];
				board[2] = board[6];
				board[6] = board[11];
				board[11] = board[15];
				board[15] = board[20];
				board[20] = board[22];
				board[22] = temp;
				break;
			case "B":
				temp = board[1];
				board[1] = board[3];
				board[3] = board[8];
				board[8] = board[12];
				board[12] = board[17];
				board[17] = board[21];
				board[21] = board[23];
				board[23] = temp;
				break;
			case "C":
				temp = board[10];
				board[10] = board[9];
				board[9] = board[8];
				board[8] = board[7];
				board[7] = board[6];
				board[6] = board[5];
				board[5] = board[4];
				board[4] = temp;
				break;
			case "D":
				temp = board[19];
				board[19] = board[18];
				board[18] = board[17];
				board[17] = board[16];
				board[16] = board[15];
				board[15] = board[14];
				board[14] = board[13];
				board[13] = temp;
				break;
			case "E":
				temp = board[23];
				board[23] = board[21];
				board[21] = board[17];
				board[17] = board[12];
				board[12] = board[8];
				board[8] = board[3];
				board[3] = board[1];
				board[1] = temp;
				break;
			case "F":
				temp = board[22];
				board[22] = board[20];
				board[20] = board[15];
				board[15] = board[11];
				board[11] = board[6];
				board[6] = board[2];
				board[2] = board[0];
				board[0] = temp;
				break;
			case "G":
				temp = board[13];
				board[13] = board[14];
				board[14] = board[15];
				board[15] = board[16];
				board[16] = board[17];
				board[17] = board[18];
				board[18] = board[19];
				board[19] = temp;
				break;
			case "H":
				temp = board[4];
				board[4] = board[5];
				board[5] = board[6];
				board[6] = board[7];
				board[7] = board[8];
				board[8] = board[9];
				board[9] = board[10];
				board[10] = temp;
				break;	
			}
			
			State newState = new Main.State(State.this, action, new String(board));
			return newState;
		}
		public boolean solvable(int limit){
			char[] board = boardStr.toCharArray();
			char[] center = {board[6],board[7],board[8],board[11],
					board[12],board[15],board[16],board[17]};
			int[] count = new int[3];
			for(char c: center){
				count[c-'1'] += 1;
			}
			int maxCount = Math.max(Math.max(count[0], count[1]),count[2]);
			if(8 - maxCount > limit){
				return false;
			}
			return true;
		}
	}
	
	static Scanner input;
	static String boardString;
	static String[] actions = {"A","B","C","D","E","F","G","H"};
	static State targetState;
	static char targetNum;
	
	
	static public void showBoard(State s){
		char[] board = s.boardStr.toCharArray();
		System.out.println("  "+board[0]+" "+board[1]);
		System.out.println("  "+board[2]+" "+board[3]);
		System.out.println(""+board[4]+board[5]+board[6]+board[7]+board[8]+board[9]+board[10]);
		System.out.println("  "+board[11]+" "+board[12]);
		System.out.println(""+board[13]+board[14]+board[15]+board[16]+board[17]+board[18]+board[19]);
		System.out.println("  "+board[20]+" "+board[21]);
		System.out.println("  "+board[22]+" "+board[23]);		
	}	
	
	static public void search(State origin){	
		for(int i=1; i<1000; ++i){
			if(DepthLimitedSearch(origin, i)){
				break;
			}
		}
		String path = "";
		while(targetState.parent != null){
			path = targetState.lastOp + path;
			targetState = targetState.parent;
		}
		System.out.println(path);
		System.out.println(targetNum);
	}
	
	static public boolean DepthLimitedSearch(State curr, int limit){
		if(limit < 0 || !curr.solvable(limit)){
			return false;
		}
		if(curr.check()){
			targetState = curr;			
			targetNum = curr.boardStr.charAt(7);
			return true;
		}else{
			if(limit > 0)
				for(String act:actions){
					if(DepthLimitedSearch(curr.move(act), limit-1)){
						return true;
					}
				}
		}
		return false;
	}
	
//	static public void genTest(){
//		Random rand =new Random();
//		State o = new State(null,null,"111111112222222233333333");
//		State tmp = o;
//		for(int i=0; i<20; ++i){
//			for(int j=0; j<7; ++j){
//				tmp = tmp.move(actions[rand.nextInt(8)]);
//			}
//			System.out.println(tmp.boardStr);
//		}
//	}
		
	public static void main(String[] args) throws FileNotFoundException{

		input= new Scanner(new BufferedReader(new FileReader("E:\\workspace\\rotate\\bin\\data.txt")));
		//input= new Scanner(System.in);

		 while(true){
			 int[] board = new int[24];
			 board[0] = input.nextInt();
			 if (board[0] == 0)break;
			 StringBuilder sb = new StringBuilder();
			 sb.append(board[0]);
			 for(int i=1; i<24;++i){
				 board[i] = input.nextInt();
				 sb.append(board[i]);
			 }
			 boardString = sb.toString();
			 
			 State originState = new Main.State(null, null, boardString);
			 
			 if(originState.check()){
				 System.out.println("No moves needed");
				 System.out.println(board[7]);
			 }else{
				 search(originState);
			 }
		 }
	}
}