非线性状态空间模型与非线性自回归模型的联系

非线性状态空间模型

$$\begin{array}{ll}{r}_t& =(1-\alpha )r_{t-1}+\alpha f(A{r}_{t-1}+W_{in}{u}_t)\\ v_t& =W_{out}{r}_t\end{array}$$
其中 $r\in R^N$ 表示状态， $u\in R^d$ 表示输入， $A\in R^{N\times N},W_{in}\in R^{N\times d},f(\cdot )=tanh(\cdot )$ 组成了非线性的状态转移方程。

非线性自回归模型

$$v_t=g(u_t,u_{t-1},\dots ,u_{t-q+1})$$

两者的联系

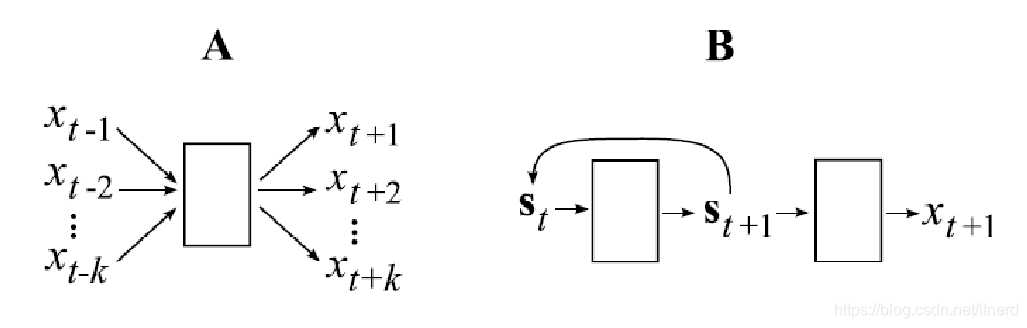
若具有如下特殊结构：
$$A={\left[\begin{array}{ll}O& O\\ I_{N-p}& O\end{array}\right]}_{N\times N}$$
$$W_{in}={\left[\begin{array}{l}W\\ O\end{array}\right]}_{N\times d},W\in R^{p\times d}$$
假设 $\alpha =1,N/p=q$
$$\begin{array}{ll}{r}_t& =f\left(\left[\begin{array}{ll}O& O\\ I_{N-p}& O\end{array}\right]r_{t-1}+\left[\begin{array}{l}W\\ O\end{array}\right]u_t\right)\\ & \\ & =f\left(\left[\begin{array}{l}W{u}_t\\ r_{t-1,1:N-p}\end{array}\right]\right)\\ & \\ & =\left[\begin{array}{c}f(W{u}_t)\\ f\circ f(W{u}_{t-1}))\\ ⋮\\ \underset{q}{\underbrace{f\circ \cdots \circ f}}(W{u}_{t-q+1})\end{array}\right]\end{array}$$

$$\begin{array}{ll}{r}_t& =f\left(\left[\begin{array}{ll}O& O\\ I_{N-p}& O\end{array}\right]r_{t-1}+\left[\begin{array}{c}{W}_1\\ ⋮\\ W_q\end{array}\right]u_t\right)\\ & \\ & =\left[\begin{array}{c}f(W_1{u}_t)\\ f(f(W_1{u}_{t-1})+W_2{u}_t)\\ ⋮\end{array}\right]\\ & \\ & =F(u_t,u_{t-1},\dots ,u_{t-q+1})\end{array}$$
因此
$$v_t=W_{out}F(u_t,u_{t-1},\dots ,u_{t-q+1})\triangleq g(u_t,u_{t-1},\dots ,u_{t-q+1})$$
即把状态空间模型转化成了自回归模型。