自适应多密钥图像加密

面向数字图像安全的自适应最优多密钥加密

摘要

数字图像安全在共享通信模型中是一项重要且具有挑战性的任务。通常，高安全的工作环境和数据通过使用私钥和公钥的加密和解密方法进行保护。本文提出了一种用于图像安全的创新加密技术，即基于多密钥的同态加密（MHE）技术。为了提高加解密过程的安全级别，采用自适应鲸鱼优化（AWO）算法选择最优密钥。优化过程中以明文图像和密文图像的峰值信噪比（PSNR）作为适应度函数。原始图像被划分为块，并通过加密过程进行重新排列，该工作实现了最高安全性，远优于其他加密技术。从实验结果可以看出，所提模型表现出卓越的性能，具有最高的PSNR和最小的均方误差（MSE），相较于其他加密方案具有显著优势。

关键词
解密、加密、图像、优化、安全、鲸鱼优化（WO）和同态

1 引言

随着媒体应用的不断扩展，安全在通信和图像容量中正变得至关重要，而加密是确保安全的方法之一。近年来提出了多种图像数据安全方案，加密是其中一种重要的常用方法。加密过程通过引入算法将明文图像数据转换为数字图像，从而将原始图像与至少一个密钥结合。加密是应用特殊数学算法和密钥将数字数据在传输前转换为密文的过程。在解密过程中，利用科学算法和密钥从数字代码中恢复原始数据。大部分普通图像及其相邻像素的值具有强相关性（即任何给定像素的值可以根据其邻近像素的值合理预测）。因此，采用了特殊的安全系统以提供所需保护。

数字图像安全在当今数字世界中由于网络的快速发展而变得越来越重要。在现有的算法中，基于混沌的算法提出了一种有效的方法来应对快速且高度安全的图像加密所面临的难题。同态密码系统是一类特殊的密码系统，其局限性在于能够对加密数据执行加法和增量操作，而不会泄露任何有关感兴趣数据的信息。同态加密似乎是保护外包应用隐私的一种良好方法，尤其是在处理整数数据类型时。然而，由于分布式计算中的数据类型不同，如何在不同类型中使用同态加密仍然是一个具有挑战性的问题。例如，由于摄影设备的普及，每天都会产生大量数字图像。这已成为用户最受欢迎的个人数据类型之一。该模型并不实用，因为它需要非共谋服务器，因此仅提供弱安全保证。此外，它为每个受保护任务使用了不同的预处理。通过自举，很多时候在评估不可预测电路和更新中间密文时会消耗大部分计算时间，这极大地影响了通用运行时。提出了一种高效的加密算法，该算法满足同态性质，可对图像进行加密和解密。该图像可用于存储，并可在其上执行任务。

2 文献综述

根据文加达普尔瓦杰等人在2017年的研究，云注册为医疗服务机构提供了不同的管理服务，其中数据存储在云中。云的三个关键部分是执行、可访问性和安全。因此，需要高效的同态加密算法。本文提出了一种高效的同态加密算法，用于加密医疗图像，并在其上执行有价值的活动而不破坏机密性。

2017年，杨等人提出了首个密钥同态加密（IGHE），该技术被开发用于图像编码。IGHE能够高效地对打乱的浮点数进行操作，以适应图像处理服务的需求。通过将传统图像处理方法转化为对加密像素的操作，可实现对加密图像的同态处理。因此，管理员可直接处理加密图像，解密后的结果与对明文图像进行处理的结果相同。为说明该研究方案，本文给出了三个常规的图像处理应用场景。实验表明，该方案安全、准确，且足以应用于实际的图像处理应用中。

2015年，辛格兄弟提出了一种指数级难度的问题，即理解椭圆曲线离散对数问题。在椭圆曲线密码学中，与其他依赖于整数分解或离散对数问题的加密方法相比，其以较小的密钥尺寸提供了更高的安全水平。在本文中，研究人员采用了椭圆曲线密码学对数字图像进行加密、解密和数字签名，以提供真实性和合法性。

WOA是由马法尔贾和米尔贾利于2014年提出的一种新算法，目前尚未被刻意应用于特征选择问题。本文提出了两种两阶段的WOA算法变体，用于搜索用于分类的理想元素子集。在第一种方法中，研究人员旨在研究在搜索过程中使用锦标赛选择和轮盘赌选择组件相较于使用随机算子的影响。在第二种方法中，采用了混合和转换操作机制以提升对WOA算法的利用效率。所提出的方法在标准基准数据集上进行了测试，并与三种算法——粒子群优化（PSO）、遗传算法（GA）和蚁狮优化器（ALO）——以及五种标准滤波式特征选择方法进行了比较。该论文还对所提方法的参数设置进行了广泛的分析。

2016年，哥帕拉克里希南和拉马克里希南提出了多重混沌映射，用于置乱和扩散以加密图像。图像加密过程重复进行四轮，且在每一轮中选择不同的密钥以抵抗已知明文攻击。该方法对黑白和彩色图像均进行了加密，并实现了较高水平的安全性。可能发生的仿真测试包括密钥空间分析、密钥敏感性分析、直方图分析、数量分析、相关系数和平行关联分析、信息熵分析以及差分攻击分析。

2018年，张等人提出了明文攻击的假设。在这项研究中，分析了一个强扩散组件的安全性，该组件被用作基于前述复杂强大现象的一些图像密码系统中的核心密码原语。该研究从理论上发现，无论密钥调度过程如何帮助增加数据的复杂性，都可以从这些分布中恢复相应密钥的每个组成部分。所提出的分析方法通过数值示例进行了验证。

在电子商务市场和客户产品评论的在线排名分析中，一篇论文利用聚类方法进行观点挖掘。模糊专家系统用于设计分层的软件可用性模型以预测实时拍卖门户和软件开发生命周期模型。古普塔和坎纳的研究讨论了实时拍卖和SDLC数据集。已提出并实施了多种生物启发算法，以有效提取基于软件的可用性模型特征，例如改进的乌鸦搜索算法、改进的二进制蝙蝠算法以及改进的鲸鱼优化算法。使用灰狼优化识别出了甲状腺疾病的最优特征。疾病预测可以被同步并唯一识别。

兰等人提出的开发框架可以通过ICS生成更多复杂的混沌映射。为了展示ICS的有效性，还基于ICS概述了一种图像加密方案。对多种类型的图像进行的仿真结果以及广泛的安全分析表明，提出的方法在图像加密方面具有良好的性质。

3 图像安全中的现有问题

由于在大规模数据集中使用传统隐私保护策略，导致出现可扩展性差和无能问题。

• 现有的安全系统还使用加密或隐写术，或它们的组合。图像加密具有一种独特、可安全保护且完美的解决方案，能够防止未授权访问。
• 如果未授权用户试图窃取存储的数据，则必须撤销其权限，但现有的加密方法并不支持用户撤销机制。

在高级加密标准中，每个块的加密过程都是以类似的方式持续进行加密，这使得编程实现较为困难。计数器模式在考虑性能和安全性的前提下，编程实现也较为困难。

• 加密和解密应足够快速，以免影响系统性能。用于加密和解密的算法必须足够简单，以便用户在PC上完成。

4 方法论

图像加密算法可以成为图像传输过程中不可或缺的一部分，以确保其有效性，同时保持最高安全级别。由于当今数字世界中网络的快速发展，数字图像安全变得越来越重要。我们提出的方法论首先将原始图像的感兴趣区域（ROI）划分为随机数量的块，随后在图像内部对这些块进行打乱。图像中存在的可理解信息是由于图像元素在特定排列下的相关性所致。为了实现图像安全，采用了多密钥同态加密（MHE）方法，该方法在图1中进行了图示展示。这是一种用于图像安全和隐私保护的新技术。

在不解密的情况下计算加密数据，其结果与从原始图像获得的“确定结果”相同。大多数情况下，加解密过程利用私钥和公钥进行MHE，以实现更好的图像安全，并通过AWO算法对密钥进行优化。该优化旨在推动发送‐接收方法中加密安全的私钥和公开密钥的性能提升。在解密策略之后，输出图像最终被还原为原始图像，以便使用峰值信噪比熵对其执行效果进行评估。该技术旨在通过降低图像组件之间的关联性并提高其熵值，来提升编码图像的安全级别。

4.1 感兴趣区域（ROI）用于图像

它是图像中滤波器执行其他操作的一部分。通过创建二值掩码，感兴趣区域（ROI）是一种二值图像，其大小与需要处理的图像相同。在掩码图像中，表示感兴趣区域的像素被设置为1，其余所有像素被设置为0。

4.2 图像安全阶段

图像加密算法可以成为图像传输过程中的基本组成部分，特别是在它们旨在提高效率的同时还能保障最高安全级别的情况下。以下小节简要描述了四种对称图像加密算法。所提模型使用MHE与理想密钥进行图像安全处理。

4.3 基于多密钥的同态加密（MHE）

语义安全的同态公钥加密方法是解决一些安全多方计算问题的核心密码工具。同态特性有助于构建具有高安全性数据恢复方案的安全系统。这些加密框架可用于对编码数据执行操作而无需知晓私钥（即无需解密），也就是说，客户是密钥的唯一持有者。

同态评估算法考虑了在N个密钥下加密的多项式多个密文图像，以及相关的评估密钥，并生成一个密文图像。多重加密是转换原始消息的唯一方法。

通过多次执行相同或不同的算法过程进行加密，可将数据转换为混乱的形态。这被称为级联加密、级联加密以及多重加密。在实验过程中，加密和解密是通过多个密钥完成的。所提出的MHE包含三个阶段：多密钥生成、最优密钥确定以及加解密技术。

4.3.1 密钥生成

密钥用于加密或解密正在被加密/解密的数据。该系统使用对称密钥进行编码与解码密钥及关联图像；同时提供了保密性和信任值安全。多密钥集合中的私钥（prk）和相应的公钥（puk）如图2所示。

使用非对称密钥算法进行密钥匹配；在此，为MHE生成多个密钥K={K1,K2,.....Kn}。在某些情况下，密钥通过随机数生成器随机生成。为了从多个密钥中选择最优密钥，将采用优化技术。

4.4 多密钥优化

优化的动机在于增强图像加解密过程中密钥选择的安全性。最后，将最佳加密帧选为最终的加密帧。为了改进多密钥集中的私钥和公钥，采用自适应狼群优化（AWO）。随后，利用变换算法尽可能地增强加密过程。最终，将最优加密内容选为最终的加密内容。WO算法、自适应过程及系统的动机在下一节中进行了描述。

4.4.1 鲸鱼优化(鲸鱼优化)

鲸鱼优化源于鲸鱼的行为。座头鲸最引人注目的特点是其个体捕猎策略。这种觅食行为被称为气泡网捕食策略。然而，在狼群优化中，当前的最优候选解被设定为目标猎物或接近最优解的位置。从根本上说，气泡网诱捕/追逐行为可以这样理解：座头鲸先潜入水下10‐15米的深处，随后开始以螺旋形状向上释放气泡包围猎物，然后跟随气泡上升至水面。

目标函数
该多密钥优化过程将适应度函数视为具有较高重建图像质量的峰值信噪比（PSNR）。该算法适用于放大多种线性和非线性问题。正确图像矩阵的维度与退化图像矩阵的维度必须相同。我们提出的密钥优化过程，以峰值信噪比（PSNR）作为衡量标准，描述如下：
$$ F_i = \text{Max}(PSNR) \quad (1) $$

(i) 为MHE初始化鲸鱼（多个密钥）
这里，密钥值指的是随机值 $ K_i (i= 1, 2, 3…n) $，其中“n”表示密钥值总数。第一阶段还包括在所提算法运行过程中对不同参数使用的手动分配特征进行整合，并初始化鲸鱼的系数向量，例如 y, Y, 和 S
$$ K = { K_1, K_2, ..... K_n } \quad (2) $$
鉴于此，鲸鱼密钥解会为每个图像块解计算峰值信噪比，若获得最佳适应度，则程序结束；若未达到理想结果，则通过以下更新机制刷新新的私钥和公钥解。

(ii) 包围猎物
座头鲸能够感知猎物位置并包围它们。对于搜索空间中理想设计位置不明确的情况，在WO算法中，当前最优竞争解即为目标猎物或接近理想设计。一旦确定了最优搜索代理，其他搜索智能体将因此努力将其位置更新至最优搜索代理
$$ \vec{U} = | S \cdot \vec{K^ }(t) - \vec{K}(t) | $$
$$ \vec{K}(t+ 1) = \vec{K^ }(t_{\text{best}}) - Y \cdot \vec{U}. $$
上述条件下，S = 2·r 和 Y = 2·l·r - l，其中“l”在迭代过程中从2减小到0，搜索智能体的新位置可以位于智能体的原始位置与当前最优智能体位置之间的任意位置。

(iii) WO的自适应函数
新解旨在实现理想适应度，整合包含较少参数依赖性的最佳特征。无需描述初始参数、步长或朝向理想解的位置。根据其在迭代过程中的函数适应度值，确定获得通用概率函数的系数向量 “y”
$$ y \Rightarrow \text{Probability} =
\begin{cases}
C_1(f_{\text{max}} - f_x) / (f_{\text{max}} - F_{\text{avg}}), & f_x \geq F_{\text{avg}} \
C_3, & f_x \leq f_{\text{avg}}.
\end{cases} $$
这里，$ f_{\text{min}} $ 和 $ f_{\text{max}} $ 是最大和最小适应度函数，而 $ C_1 $ 和 $ C_3 $ 的取值范围为 (0, 1)。在整个迭代过程中，位置根据其函数适应度值自适应地向理想解变化。因此，元启发式算法在结合自适应系统后，能够以更少的计算时间实现理想解、邻近极小值逃逸以及更快的收敛速度。

(iv) 气泡网攻击方法
为了数学上描述座头鲸的气泡网行为，采用了两种增强方法。气泡袋网策略可通过两种方法实现。第一种是收缩环绕，可通过减少对系数向量的估计来实现。

开发阶段
螺旋方程用于模拟座头鲸的螺旋框架式前进，该方程描述了鲸鱼位置与猎物之间的关系，可表示如下：
$$ \vec{K}(t+ 1) = e^{bt} \cdot \cos(2\pi \cdot y) \cdot \vec{U’} + \vec{K^*}(t). \quad (3) $$
需要注意的是，座头鲸在捕食时会沿着收缩圆内部围绕猎物游动，同时以蜿蜒路径行进。为了体现这种同步行为，在优化过程中期望以50%的概率在收缩包围系统和螺旋模型之间进行选择，以更新鲸鱼的位置。其数学模型如下：
$$ \vec{K}(t+ 1) =
\begin{cases}
\vec{K}(t) - y \cdot \vec{U} & \text{if } p < 0.5 \
\vec{U’} \cdot e^{bs} \cdot \cos(2\pi s) + \vec{K}(t) & \text{if } p \geq 0.5,
\end{cases}
\quad (4) $$
其中 $ \vec{y} $ 为−1到1之间的随机值，展示了这种同步行为，同时也表明在优化过程中，有50%的概率在收缩包围系统和螺旋模型之间进行选择，以恢复鲸鱼的位置。

探索阶段
在向量选择方面，可采用一种比较方法来搜索猎物（探索）。总体而言，座头鲸根据彼此的位置进行无目的游走。为了获得整体分析器，请求管理员由一个随机选择的搜索专家激活，而不是最优搜索算子
$$ \vec{U} = | \vec{S} \cdot \vec{K} {\text{rand}} - \vec{K} | \quad (5) $$
$$ \vec{K}(t+ 1) = \vec{K} {\text{rand}} - \vec{Y} \cdot \vec{U}. \quad (6) $$
因此，使用随机值的概率高于1或低于−1，以迫使搜索智能体远离参考鲸鱼。在探索阶段，不同于开发阶段，搜索专家的位置会根据随机选择的搜索算子而非迄今为止发现的最优搜索算子进行更新。该系统 $ |\vec{Y}| > 1 $ 强调探索能力，使WO算法能够实现全局最优，并 $ |\vec{Y}| > 1 $ 用于激活搜索智能体的位置。

(v) 终止准则
该过程重复进行，直到达到较高的迭代次数。新的解集根据上述更新步骤进行评估和跟踪，直至满足停止准则。

4.4.2 加密

同态加密是一种对明文图像和密文图像均采用相同代数函数进行处理的加密方式。同态加密使得服务器能够在不知道原始明文图像的情况下，对加密数据执行操作。用户利用密钥对私最钥优图像并创建prk和puk−最优以及，连同公钥（puk），该密文图像将被发送到服务器。puk=（k，i）和K=（p，q）Enc（I，prk）以选取随机变量 $ r \in Z^*_k $，计算密文数据 $ c = I \cdot r^k \mod k^2 $。

一种加密算法最近对原始图像的秘密图像非常有效。在加密过程中，建议使用锁来编码图像的每个像素。该MHE‐AWO过程如图3所示，可将其视为图像位，以获得密文图像。

4.4.3 解密

在解密策略中，包含加密像素的图像通过 $(p, q)$ 和秘密向量进行处理。解密过程采用两个掩码，即秘密掩码和偶数掩码，以稳定递进的方式进行。用于从密文图像和其他秘密参数中解密消息位（像素值）$ m $。

4.4.4 评估

同态操作，例如加法和乘法，可以在编码图像上执行，从而生成新的加密图像，对该加密图像进行解密将输出具有相似功能的结果。同态任务可以关联到查看两个编码图像的像素。

所提模型获取原始图像进行安全处理，从这些图像中提取感兴趣区域，生成用于同态加密的多个密钥，进行多密钥优化过程，执行WO更新过程，通过自适应函数选择最优密钥 $ prk \Rightarrow {1, 2, …, n} $ 和 $ puk \Rightarrow {1, 2, …, n} $，执行基于最优密钥的加密和解密。

5 结果与讨论

5.1 实验结果

所提出的图像安全模型在MATLAB 2016a中运行，使用i5处理器和4GB内存。采用不同的测试图像来评估所提出图像安全方法的性能。仿真模型选用四幅标准图像Lena、房屋、Pepper和狒狒，取得了较好的结果。这些图像来自USC-SIPI图像数据库。表1展示了Lena、Pepper、狒狒和房屋的原始图像、加密图像和解密后的图像的实验结果。

5.2 性能分析

所提出的方案通过使用一些指标（如PSNR、MSE、CC和熵）进行了评估，并与传统加密和优化方法进行了比较。

$$
\text{Peak Signal to Noise Ratio (PSNR)} = 10 \log_{10}\left( \frac{(255)^2}{\text{MSE}} \right) \quad (7)
$$

$$
\text{Mean Square Error (MSE)} = \frac{1}{N} \sum (P_{\text{Act}}(i,j) - P_{\text{encry}}(i,j))^2 \quad (8)
$$

$$
\text{Entropy} = \log(\log(P(E_s))) \ast \frac{N_{\text{edges}}(E_s)}{l \cdot m} \ast H_{\text{entropy}}(E) \quad (9)
$$

$$
\text{Correlation Coefficient (CC)} = \frac{\text{CON}(x, y)}{\sqrt{\text{mean}(x) \ast \text{mean}(y)}} \quad (10)
$$

$$
\text{密钥敏感性} = \frac{\text{正确密钥数量}}{\text{正确密钥} + \text{错误密钥}} \quad (11)
$$

表2展示了所提出的（MHE-AWO）图像安全结果。针对四幅标准图像，分别列出了各指标的性能，即熵、峰值信噪比、相关系数、均方误差、熵以及密钥敏感性。此外，首先在第一行显示了原始图像，在后续的图示部分中展示了通过MWO算法获得的加密图像。然后对图像的安全性表现进行了评估。分析基于不同密钥长度的敏感性结果，并得出最大敏感度水平为82.33%。例如，Lena图像的PSNR、CC、MSE和熵分别为64.93、0.9983、0.020和7.6554，其他图像的结果也如上表所示。

表2 所提模型的图像安全分析

图像	PSNR	CC	MSE	熵	密钥敏感性
Lena	64.93	0.9983	0.020	7.6554	83.22
Pepper	65.75	0.9988	0.017	7.5256	84.08
狒狒	67.194	0.9998	0.031	7.7719	79.5
房屋	58.14	0.9965	0.099	7.7751	76.22

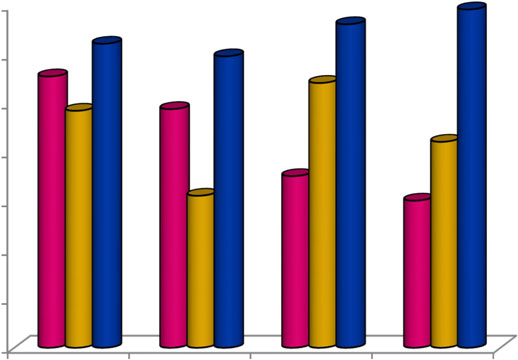
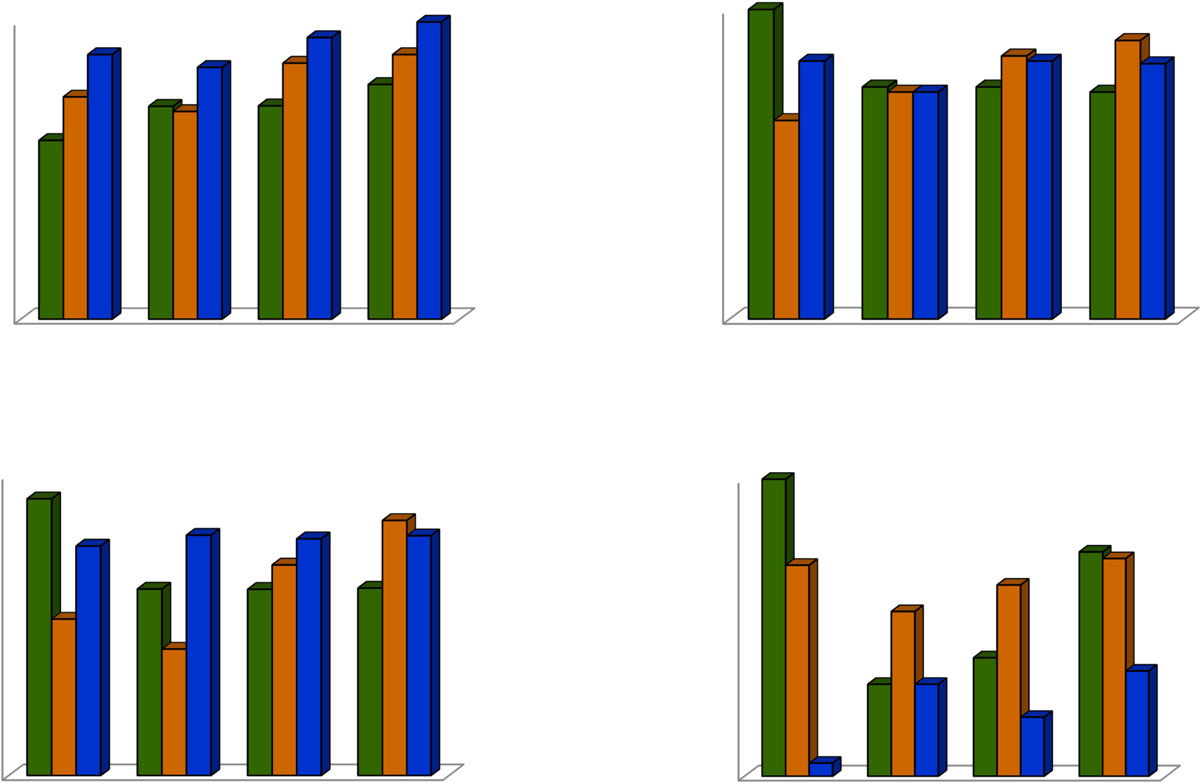
图4展示了使用HE、MHE和MHE-AWO等不同策略对图像安全进行的相对检验。图4A显示了各种图像的PSNR，其中MHE-AWO对应的最高值为67.194 dB。在基于密像的方法中，通过加密和解密来恢复原始图像。此外，熵、均方误差和相关系数值分别在图4B、C和D中进行了说明。从均方误差值可以看出，它反映了原始图像与解密后图像之间的差异，且该值应尽可能低。通过使该技术能够更好地加密多媒体数据或任何其他需要安全传输的信息，此过程可以进一步改进。

图5展示了各种优化方法的适应度评估，例如遗传算法GA、WO和AWO。在椒盐图像的迭代中，AWO达到了最高的适应度。在此，对四幅图像进行了PSNR检验，其中AWO的表现优于遗传算法，其估计值为45.28。分析了所提模型与现有算法在不同图像上的执行时间。最后，如图6所示，该安全流程在加解密过程中所需的对比执行时间最短。上述方法已通过多种编码与解码图像的评估研究进行了验证。

表3 攻击应用结果

原始图像	被攻击	PSNR	CC	MSE	熵
		48.22	0.9912	0.078	6.7851
		52.75	0.9898	0.087	7.1387
		56.89	0.9900	0.061	6.9719
		45.57	0.98725	0.147	6.5946

当攻击应用于不同图像时，所提策略图像的峰值信噪比估计值更高。在不同图像上应用攻击后的峰值信噪比估计值与所提策略进行对比，85.65%恢复了原始图像。当计算相关系数时，其值为1时，其图像质量在提出的方法中得以保持，并且应用了攻击。通常情况下，图像质量受其图像清晰度影响，而图像清晰度未被保持。

6 结论

本文提出了一种基于最优密钥的MHE加密图像的数字图像安全操作分析模型。结果表明，在应用加密技术之前，使用基于块的变换方法可提高图像安全。所提策略的性能通过执行时间分析和安全级别评估方法进行评价。从实现结果来看，该策略明显实现了最低的加解密时间。在所提技术中，针对所有标准图像，以峰值信噪比作为适应度函数得到了理想检验。所提系统的执行情况还根据通信时间对监听方面进行了探讨。所提安全工作的缺点在于选择公钥和私钥选择模型时消耗了最大计算时间。因此，未来我们将主要关注更高级别的安全研究，并探索新型启发式算法以提升MHE的执行效率。