增强型电路平均建模技术

采用增强型电路平均技术对非理想低功率PWM DC‐DC转换器在连续导通模式和断续导通模式下进行精确建模

1. 引言

对于集成电路和系统的电子设计自动化（EDA）而言，电路设计人员能够获得不同复杂程度的元件和系统模型，并将其应用于广泛的应用场景中，这一点尤为重要。通常，模型复杂度的权衡体现在计算时间与精度之间。复杂的详细模型旨在精确地描述器件的物理行为。然而，使用此类模型进行仿真时，由于模型规模较大且需要精细的时间分辨率，通常会导致较高的CPU成本。对于某些类型的电路，例如在开关电源转换电路中，设计人员可能更关注电路的整体性能，而非获取详细的时域波形。在这种情况下，如果认为开关周期很短，则可以使用紧凑电路宏模型准确预测开关转换器的基本工作特性。特别是，时域开关转换器模型可以捕捉关键的设计特性，如开关纹波、对负载或输入瞬态的响应以及小信号频率响应 [Vorperian 1990a]。通过这些紧凑电路模型，并忽略开关过渡过程中不必要的细节，可以利用通用的计算机辅助设计（CAD）工具高效地完成多个开关周期的仿真。

电路平均模型长期以来一直被用于预测电力电子转换器的动态和稳态响应 [Vorperian 1990a, 1990b；Maksimovic 等 2001]。平均法是一种系统化的方法，可获得简化模型，专注于逐周期行为，而无需考虑开关周期的细节。平均方法包括基于方程的平均状态空间模型 [Davoudi 等 2006]，以及依赖于建立等效平均电路模型的电路平均技术 [Maksimovic 等 2001]。这些技术提供了物理洞察，并有助于建立可用于设计过程的解析关系，以根据给定的设计要求和性能指标选择元件和控制器参数值 [Maksimovic 等，2001；Sanders 和 Verghese 1991]。然而，这些模型中的大多数是为建模片外转换器的性能而开发的，这些转换器通常用于控制流向大型设备和电器的功率。此外，文献中提出的大多数模型依赖理想或线性化元件来模拟电路中存在的损耗和非理想特性 [Kovar 等，2009；Nirguade 等 2001]。这是一个显著的局限性，特别是在低功率电子转换器的情况下，因为这些模型无法涵盖微电子电路的许多性能特性。

在本文中，我们首次提出了一种增强型电路平均模型，该模型经过优化，可用于准确捕捉脉宽调制（PWM）DC‐DC变换器的动态行为，特别是在低功耗集成电路（IC）应用中。该增强模型采用非线性受控源和元件，以准确描述变换器中半导体器件的非理想特性。更具体而言，我们的增强模型能够考虑二极管和MOS晶体管在转换器工作过程中的非理想行为，从而相比文献中传统的PWM电路平均模型显著提高了分析结果的精度。我们将证明，所提出的模型在不同工作条件下均能良好地适用于大信号和小信号动态仿真。我们还将展示如何通过引入对亚阈值漏电流效应的建模来进一步提升模型的精度。此外，我们提出了一种技术，可通过基于仿真的器件表征方法，从工业标准器件模型（如BSIM4 [Dunga等 2006]）中自动提取所提出模型的器件参数，以进一步提高精度。最后，我们的新型建模方法具有较强的通用性，可应用于连续导通模式（CCM）和断续导通模式（DCM）下的降压型和升压型转换器，以及标准配置和同步配置，这对于低功率应用尤为重要。该新方法能够同时捕捉大信号和小信号动态行为，使其易于集成到通用电子设计自动化（EDA）工具中。需要特别指出的是，增强模型在提升精度的同时，并未给使用该模型的仿真带来显著的计算开销，从而保留了电路平均技术所具有的低CPU成本优势。当使用标准行为级建模语言（即Verilog‐A）进行编码时，我们的模型相较于耗时的晶体管级仿真，提供了超过一个数量级的运行时间加速比。因此，如本工作所采用的电路平均法，成为电路设计人员研究用于低功率应用的开关模式 DC‐DC变换器动态特性的一种高效实用工具。

2. PWM DC‐DC转换器的精确建模

电路平均模型长期以来一直被用于预测电力电子转换器的动态和稳态响应。然而，文献中提出的大多数模型都是采用理想或线性化元件来建模电路中存在的非理想器件，以保持模型的简洁性和高效性。

本文提出了一种增强型电路平均模型，该模型通过使用平均量的非线性表达式来对电路中的非理想器件进行建模，从而获得更精确的结果。本节首先概述了我们对非线性二极管和晶体管表达式的建模方法，然后介绍所提出的增强型电路平均模型及其方程。模型的详细推导借助示例转换器电路进行说明更为清晰。除非另有说明，本节将以图1(b)所示的标准降压转换器为例，其工作在连续导通模式（CCM），开关波形q(t)如图1(a)所示。随后，在给出详细推导的基础上，将进一步展示适用于工作在连续导通模式（CCM）和断续导通模式（DCM）下的PWM转换器以及同步拓扑结构的通用化模型。所提出的精确模型可用于多种类型的分析，包括大信号仿真（用于计算工作点和稳态纹波）、小信号仿真以及动态行为的仿真。

2.1. 非理想器件的建模

所提出的增强型电路模型适用于一般的电路非理想性。本文重点讨论集成电路（ICs）中通常存在的两种非线性半导体器件，即PN结二极管和MOS晶体管。这些器件对模型的精度影响最大。

2.1.1. 二极管

半导体PN结二极管是开关电源转换电路中通常存在的基本元件之一。二极管电流 $I_D$ 与二极管电压 $V_D$ 之间的关系为
$$
I_D = I_s(e^{V_D / nV_T} - 1) \approx I_s e^{V_D / V_T}.
\tag{1}
$$
在此关系中，$I_s$ 是饱和电流，$V_T$ 是热电压。对于微电子电路而言，$I_s$ 通常在 $10^{-15}$ 安培范围内，这会在正常工作条件下产生显著的正向压降。典型的平均模型为这种关系包括理想二极管模型（具有零电压降）、恒定压降模型（具有固定电压降）和小信号模型（具有线性电流‐电压关系）[Sedra 和 Smith 2009]。对于低功率应用，这些传统模型所提供的精度是不够的。当在模型中包含非线性电流‐电压关系时，可以获得更高的精度，这正是我们方法的主要目标。对于我们的模型，将平均二极管电压 $\bar{V}_D$ 表示为平均电流 $\bar{I}_D$ 的函数更为方便，如下所示：
$$
\bar{V}_D \approx V_T \ln\left(\frac{\bar{I}_D}{I_s}\right).
\tag{2}
$$
在此关系中，我们假设对数的平均值近似等于平均值的对数。在这种情况下，这是一个合理的假设，因为 $I_D(t)$ 与其平均值偏离不大。

2.1.2. MOS晶体管

在PWM转换器中，有源功率开关通常使用由占空比固定的PWM信号驱动的MOS晶体管实现，并在其导通时偏置工作于三极管区。传统的平均模型要么假设无电压降（理想开关情况），要么对电流‐电压关系进行线性化。为了获得更精确的平均模型，我们将MOS器件的电流‐电压关系作为非线性电阻处理，该非线性电阻将平均电压降与平均漏极电流关联如下：
$$
I_d = f(V_{DS}) = k’(W/L) V_{OV}(V_{DS} - \frac{1}{2} V_{DS}^2)
\tag{3}
$$
$$
\bar{V} {DS} = f(\bar{I}_d) \approx \frac{\bar{I}_d}{k’(W/L) V {OV}},
\tag{4}
$$
其中 $k’$ 和 $(W/L)$ 为晶体管参数，而 $V_{OV} = V_{GS} - V_{th}$ 和 $V_{DS}$ 分别为过驱动电压和漏源电压，$I_d$ 为晶体管漏极电流 [Sedra 和 Smith 2009]。需要指出的是，尽管我们在模型中仅关注了每个二极管和MOS晶体管的一种非理想性的影响（如公式(2)和(4)所示），但也可以采用类似的方法将其他非理想性的影响纳入模型，以进一步提高其精度。一个例子是亚阈值漏电流的影响，我们将在第4节中进行说明。

2.2. 非理想大信号PWM开关模型

2.2.1. 标准转换器

考虑图1(b)所示的降压转换器。当MOS开关由如图1(a)所示的波形 $q(t)$ 驱动时，该转换器实际上工作于两种配置之一。我们应用电路平均法来推导一个能够捕捉输出负载上大信号变化的动态模型。在此情况下，我们假设转换器的开关频率快于转换器中其他信号的时间尺度，从而这些信号的瞬态效应可以在每个开关周期内被平均掉。为简化起见，我们还将忽略通过电感电阻 $r_L$ 的小电压降。

第一种情况是晶体管导通且二极管反向截止，第二种情况是晶体管关断且二极管导通。

在一个开关周期内取平均后的电路控制方程为：
$$
L \frac{d \bar{I} L}{dt} = d_1 (\bar{V} {in} - \bar{V} {DS}) - (1 - d_1) \bar{V}_D - \bar{V} {out}
\tag{5}
$$
$$
C \frac{d \bar{V} {out}}{dt} = \bar{I}_L - \frac{\bar{V} {out}}{R_L}
\tag{6}
$$
$$
\bar{I} D = (1 - d_1)\bar{I}_L
\tag{7}
$$
$$
\bar{I}_S = d_1 \bar{I}_L,
\tag{8}
$$
其中 $d_1$ 是固定占空比变换器的开关波形 $q(t)$ 的占空比。附加变量 $\bar{V}_D$ 和 $\bar{V} {DS}$ 的额外方程分别由公式(2)和公式(4)中给出的非线性关系获得。我们还注意到，在稳态下，电感上的平均电压降和电容中的平均电流为零。公式(5)到(8)中的关系可以合并为一个等效的增强型平均电路模型，如图2所示。可以看出，电路平均模型的简洁性得以保留，同时相较于线性化或理想模型，能更好地表征半导体器件的非理想特性。

本节的推导基于图1(b)所示的标准降压转换器在连续导通模式下的工作情况。对于断续导通模式以及其他PWM转换器类型，也可进行类似的推导。为了便于在Verilog‐A等标准行为建模语言中应用该模型，图3(a)展示了适用于连续导通模式和断续导通模式的 PWM开关的混合通用精确模型。其表达式 $d_2$ 随工作模式的不同而变化，具体如下：
$$
d_2 = 1 - d_1 \quad (\text{for CCM})
\tag{9}
$$
$$
d_2 = D_{con} - d_1 \quad (\text{for DCM}),
\tag{10}
$$
其中
$$
D_{con} = \frac{2L}{T} \frac{| \bar{I} C |}{\bar{V} {AC} d_1}.
\tag{11}
$$
当 $D_{con} \leq 1$ 时，转换器工作在连续导通模式。当 $D_{con} > 1$ 时，转换器工作在断续导通模式。在这些关系中，$L$ 为电感 $L$ 的值，$T$ 为开关频率 [Ben‐Yaakov 和 Adar 1994]。

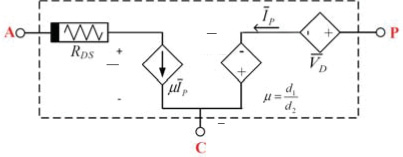
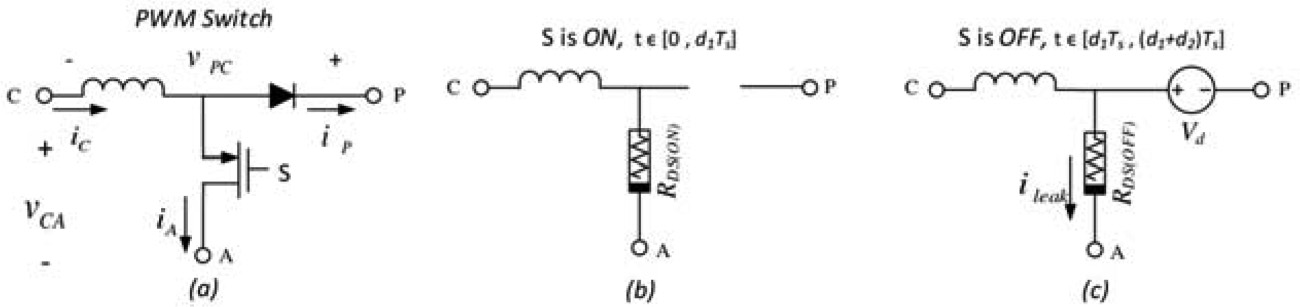
2.2.2. 同步转换器

需要注意的是，增强型电路平均模型也可以开发用于同步转换器，这类结构在低功率应用中尤为流行。同步转换器结构采用两个开关，而不是一个开关和一个二极管。通过考虑额外MOS器件的器件级非理想效应，而非二极管的效应，并假设开关之间的过渡“死区”时间可忽略且存在零电流检测电路 [Chen et al. 2008; Yousefzadeh and Maksimovic 2006]，可以建立与标准转换器基本相似的建模方法。在这种情况下，在推导公式(5)至(8)时，$V_{DS}$ 被替换为 $V_{DS1}$，而 $V_D$ 被替换为 $V_{DS2}$，以表示与两个MOS器件开关相关的电压降。最后，图3(a)的混合模型将在依赖源 $\bar{V}_D$ 的位置增加一个非线性电阻，从而形成如图3(b)所示的混合模型。

2.3. 非理想大信号输出纹波表达式

大多数DC‐DC变换器由于输入电压和输出负载的大信号变化而在输出端产生大信号直流纹波 [Hart 2011]。因此，我们所提出的确切模型在纹波波形的表达式中也必须考虑 $\bar{V} D$ 和 $\bar{V} {DS}$ 的影响。同样，我们基于图1(b)中的降压转换器进行详细的推导。

当金属氧化物半导体晶体管开关导通且二极管处于反向偏置时，我们可以推导出在一个开关周期内电感电流 $\Delta I_L$ 的变化表达式。假设电流呈线性变化，则在晶体管的开通和关断周期内，电感电流的变化可表示为：
$$
(\Delta I_L) {ON} = \frac{(V_S - V {DS} - V_{out}) d_1 T}{L}
\tag{12}
$$
$$
(\Delta I_L) {OFF} = \frac{(-V_D - V {out})(1 - d_1) T}{L},
\tag{13}
$$
其中 $d_1$ 为之前的占空比，$T$ 为开关周期。

输出端纹波电压的表达式由电容 $C$ 上的电荷量 $Q$ 的两个关系式得到。第一个是电容的电荷‐电压关系，该关系源自电容的定义，即 $\Delta Q = C \Delta V_{out}$。第二个关系来自电荷与电容电流之间的关系。由于电容的稳态平均电流为零，降压转换器中电容电流的波形将与通过电感的电流成比例变化 [Hart 2011]。将这两个关系式与公式(13)结合，可得
$$
\Delta V_{out} = \frac{T \Delta I_L}{8C} = \frac{T}{8LC} (-V_D - V_{out})(1 - d_1)T.
\tag{14}
$$

现在可以通过对公式(14)中的表达式进行平均法处理，得到输出纹波电压的平均值，结果如下：
$$
\Delta \bar{V} {out} = \frac{(1 - d_1)(\bar{V}_D + \bar{V} {out})}{8LCf^2}.
\tag{15}
$$
公式(15)中的表达式可用于在利用第2.2节和第4节中提出的平均模型确定大信号工作点后，对变换器输出端的稳态大信号纹波波形进行改进估计。对于其他标准PWM变换器拓扑，也可推导出类似的表达式。

2.4. 非理想小信号动态PWM开关模型

与之前推导的大信号模型不同，为了表征占空比的变化，需要做出小信号假设，因为转换器工作本质上依赖于占空比。一旦确定了稳态工作点，就可以建立小信号动态模型，以跟踪占空比或电源电压 [Maksimovic等 2001] 的小幅变化。在这种情况下，如果 $\hat{v}_s(t)$ 和 $\hat{d}(t)$ 分别表示相对于稳态电源电压和占空比的小偏差，则有
$$
V_S(t) = V_S + \hat{v}_s(t)
\tag{16}
$$
$$
d_1(t) = d_1 + \hat{d}(t).
\tag{17}
$$

一旦所有瞬态过程结束后，与变换器相关的电压和电流也将由平均大信号工作点值加上小信号交流变化组成。通过将电压和电流的复合关系代入方程（5），并忽略直流项（由于稳态下电感电压为零，这些直流项之和为零），同时根据小信号假设忽略二阶交流项，所得表达式变为
$$
L \frac{d\hat{i}_l(t)}{dt} = d_1 \hat{v}_s(t) + \hat{d}(t)V_S - \hat{v}_o(t) - (1 - d_1)\hat{v}_d(t) + \hat{d}(t) \bar{V}_D
\tag{18}
$$
$$
C \frac{d\hat{v}_o(t)}{dt} = \hat{i}_l(t) - \frac{\hat{v}_o(t)}{R_L}
\tag{19}
$$
$$
\hat{i}_s(t) = \hat{d}(t)\bar{I}_L + d_1 \hat{i}_l(t).
\tag{20}
$$

这些方程可以使用等效的小信号电路模型进行建模，如图4所示。

3. 基于仿真的器件表征

在第2.1节中，我们通过使用公式(2)和(4)中给出的非线性表达式，对二极管和晶体管的时间平均行为进行了建模。虽然这种方法虽然精确且简单，但也存在一些局限性。首先，它是一种特定器件的方法，这意味着为了评估公式(2)和(4)中的非线性表达式，需要针对不同的工艺和技术重新计算二极管和晶体管参数。这使得任意电路和器件的器件模型参数计算难以自动化。此外，公式(2)和(4)中的关系仅捕捉了非理想器件最基本的特性行为，从而限制了使用该模型进行仿真时的精度。

为了解决这些问题，本文提出了一种基于仿真的器件表征新方法。该方法能够在平均电路的仿真过程中，精确且自动地计算二极管正向压降 $V_d$ 和晶体管电压降 $V_{ds(ON)}$，同时还能量其他参数，例如第4节中介绍的亚阈值漏电流 $i_{leak}$。通过一个示例可以更好地说明该方法。考虑计算MOS晶体管器件的 $V_{ds(ON)}$ 的情况。图5(a)显示了一个升压转换器，其中晶体管 $Q_1$ 处于导通状态，其栅源电压为 $V_s$，漏源电流为 $I_{ds(ON)}$。图5(b)展示了在平均电路仿真过程中用于评估 $V_{ds(ON)}$ 的电路。该电路设计成使 $Q_2$ 的尺寸、栅源电压和漏源电流与图5(a)中的情况相同，以确保在图5(b)中测得的 $V_{DS(ON)}$ 与图5(a)中 $Q_1$ 的 $V_{ds(ON)}$ 一致。使用平均电路模型可以方便地计算 $I_{ds(ON)}$ 和 $V_s$。其中，$V_s$ 就是开关信号的幅值，而 $I_{ds(ON)}$ 可通过图7确定。
$$
I_{ds(ON)} = \frac{\bar{I} {ds}}{d_1 + d_2} = \frac{\bar{I}_A}{d_1 + d_2}.
$$
可以执行基本相似的步骤来计算 $i {leak}$ 和 $V_d$。

所提出的基于仿真的器件表征方法考虑了原始晶体管和二极管器件模型中包含的所有非理想特性。因此，平均模型的精度可能与器件模型本身的精度相当。这是所提出模型相较于其他方法的主要优势之一。在本文中，我们对所有晶体管使用BSIM4模型 [Dunga等人 2006]。因此，在进行基于仿真的器件表征时，许多非理想特性，包括短沟道效应和亚阈值效应，都被考虑在内。然而，需要注意的是，该技术仅捕捉器件的直流特性，意味着由快速开关活动引起的高阶响应被忽略。这与平均电路模型的本质一致，因为平均电路模型本质上仅捕捉实际电路响应的直流（平均）分量。

4. 进一步增强：考虑亚阈值电流效应

在对图3(a)中的混合模型进行测试时，针对工作在连续导通模式和断续导通模式下的标准降压转换器，所得结果准确，并且与仿真完整变换器电路相比显著减少了计算时间，具体将在第5节中展示。然而，当该模型应用于其他一些PWM变换器拓扑和设计时，由于非理想器件的电路平均模型存在局限性，部分结果准确性有所下降。造成结果差异的一个根本原因是未考虑晶体管开关关断周期中亚阈值漏电流的影响 [Rabaey等 2003]，特别是当该漏电流与负载电流相比不可忽略时。

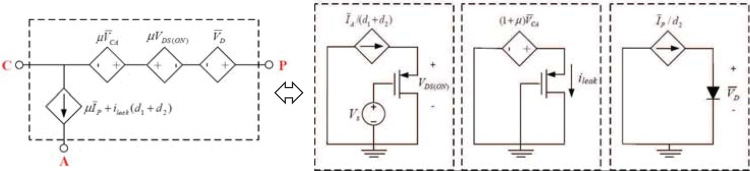
图3(a)所示PWM开关的电路平均混合模型可以进行改进，以考虑亚阈值导通的影响。在本节改进模型的推导中，我们假设变换器工作在断续导通模式，因为连续导通模式是当 $d_1 + d_2 = 1$ 时断续导通模式的一种特例。图6(b)和图6(c)分别显示了图6(a)中PWM开关在晶体管开通和关断周期内的等效电路，其中 $R_{ds(OFF)}$ 为晶体管在亚阈值导通下的等效电阻。图6中端子电流 $i_C$、$i_A$ 和 $i_P$ 在一个开关周期内的波形如图7所示。

当晶体管开关 $S$ 导通时，如图6(b)所示，端子 $C$ 和 $A$ 之间的平均电压由以下关系给出
$$
\bar{V} {CA} = \bar{V} {CA(ON)} = \frac{L \Delta i_L}{d_1 T_s} + R_{ds(ON)} \cdot i_c(ON),
\tag{21}
$$
其中 $\Delta i_L$ 是电感电流纹波的幅值，如图7所示，$i_c(ON)$ 是晶体管导通时端子 $C$ 的电流。我们将公式(21)中的关系视为在整个开关周期内的平均电压，前提是电路时间常数远大于开关周期 [Amran等 1991]。该假设同样适用于跨接在端子 $P$ 和 $C$，记为 $\bar{V} {PC}$。当晶体管关断时，如图6(c)所示，我们有
$$
\bar{V} {PC} = \bar{V} {PC(OFF)} = \frac{L \Delta i_L}{d_2 T_s} + V_d,
\tag{22}
$$
其中 $V_d$ 是二极管的正向压降。通过结合公式(21)和(22)，我们得到新PWM开关模型的电压关系：
$$
\bar{V} {PC} = \mu \cdot \bar{V} {ca} - \mu R {ds(ON)} \cdot i_c(ON) + V_d.
\tag{23}
$$
请注意，由于在推导公式(21)时所做的近似，公式(23)中给出的电压关系与值 $R_{ds(OFF)}$ 无关。实际上，$R_{ds(OFF)}$ 对电压关系的影响可以忽略不计。至于电流关系，图7中 $i_C$、$i_A$ 和 $i_P$ 的平均值分别为
$$
\bar{I} C = \left(i {pk} - \frac{\Delta i_L}{2}\right)(d_1 + d_2)
\tag{24}
$$
$$
\bar{I} A = \left(i {pk} - \frac{\Delta i_L}{2}\right)d_1 + i_{leak} \cdot d_2
\tag{25}
$$
$$
\bar{I} P = \left(i {pk} - \frac{\Delta i_L}{2}\right)d_2 + i_{leak} \cdot d_2,
\tag{26}
$$
其中，$i_{pk}$ 是电感电流 $i_L$ 的峰值，而 $i_{leak}$ 是流过 $R_{DS(OFF)}$ 的亚阈值电流。最后，$\bar{I} A$ 可被重写为
$$
\bar{I}_A = \frac{d_1}{d_2} \bar{I}_P + (d_1 + d_2)i {leak}.
\tag{27}
$$

图8显示了考虑漏电流影响的改进型PWM开关模型，而图9显示了电路平均PWM开关的统一模型，该模型由图8和基于仿真的器件表征电路组合而成。该模型可用于多种 DC‐DC变换器具有相同的结构，例如降压型、升压型和升降压型。它还支持在连续导通模式和断续导通模式下运行，如第2.2节所述。此外，对二极管和晶体管相关的电压降进行实时评估。最后，需要注意的是，尽管存在二极管和晶体管，但由于这些器件中不出现任何开关动作，因此包含基于仿真的器件特性化电路不会影响统一PWM开关模型的仿真效率。

、 ileak和Vd。)

5. 数值示例

本文提出的增强型平均模型在Cadence Virtuoso中实现，并使用Spectre结合90纳米技术进行仿真。原始转换器由晶体管级网表描述，并与工业标准的BSIM4模型接口。平均模型采用Verilog‐A编写。所提出模型的测试基于升压型和降压型转换器的组合，结合开环和闭环仿真进行。我们将所提出模型的精度和加速比与晶体管级电路的仿真结果进行比较，并讨论相较于文献中现有平均模型所取得的改进。需要注意的是，所有仿真均在配备4 GB内存和四核3.2GHz Intel Core i5处理器的Linux工作站上运行，但仅使用了一个核心。

5.1. 升压转换器开环仿真

图10(a)所示的升压转换器采用表I中给出的元件值进行测试。该转换器在负载电阻为 $5\Omega$ 时的开关频率为50千赫。原始晶体管级转换器电路和平均化电路均在启动瞬态下对变化的占空比进行了仿真。转换器的占空比由一个阶跃信号控制，使得电路以30%的初始占空比启动，然后阶跃上升至60%。在 40μs后，占空比再阶跃下降至40%。

图11显示了使用三种不同平均模型获得的输出电压和电感电流的比较。第一种模型是采用二极管和MOS开关上零电压降的简单（理想）平均模型。第二种模型是传统线性平均模型假设二极管具有恒定电压降，MOS开关具有线性电压降 [Erickson和 Maksimovic 2001]。最终的模型是所提出的平均模型。原始变换器电路的波形也在图11中提供作为参考。可以看出，与其它平均模型相比，我们的模型在精度上有显著提高。这种改进带来了一定的额外计算开销，但仿真时间仍明显快于晶体管级仿真。这一点在表II给出的数值比较中得到了清晰体现。还需要注意的是，尽管线性模型和我们所提出的模型都考虑了器件非理想性和寄生参数的影响，但它们的实现方式存在根本差异。例如，在线性模型中，$V_{DS}$ 的值通过一个电阻来表示，该电阻值在稳态仿真中测得，并在平均模型仿真过程中保持不变。而我们所提出的模型则根据电路状态在平均模型仿真期间连续测量 $V_{DS}$ 的值。可以立即看出，线性模型仅在稳态下能获得较好的估计，而在电路状态动态变化的瞬态过程中则无法准确建模。此外，使用BSIM4模型来评估 $I_{DS(ON)}$ 和 $I_{DS(OFF)}$ 的值，相较于使用器件方程进行估算，可提供更高的精度。图12展示了三种模型波形的局部放大比较，以进一步说明。使用所提出模型相对于原始变换器获得的加速比为 13×。

5.2. 降压转换器闭环仿真

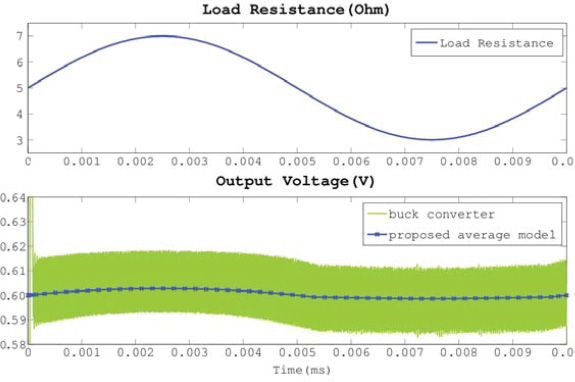
图1(b)所示的降压转换器在闭环配置下进行测试，采用表I中给出的元件值，并通过改变负载电阻来模拟负载随时间的变化。其对应的平均模型如图2所示。输入电压设置为2伏特，开关频率设置为20千赫兹。负载电阻初始值设为 $5\Omega$，随后进行正弦变化。输出电压由脉宽调制控制反馈环调节至0.6伏特。图13显示了两个电路的负载电阻和输出电压的变化情况；数值仿真数据总结于表II中。与实际的降压转换器相比，使用所提出的平均模型获得了 30× 的加速比。

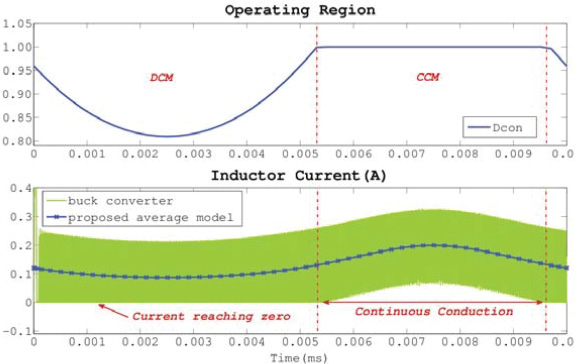
为了评估混合平均模型的鲁棒性，通过控制负载电阻使降压转换器在断续导通模式和连续导通模式之间切换。图14的上部图表显示了根据公式(11)计算得到的 $D_{con}$，该值表示转换器的工作模式。在仿真开始后 53μs ，模型从断续导通模式切换到连续导通模式，且 $D_{con}$ 达到1。如图14的底部波形显示，我们的平均模型精确地捕捉到了这一过渡过程。同时需要强调的是，所提出的平均模型的电感电流与原始电路的电感电流非常接近。

最后，对变换器输出端的大信号纹波电压进行了比较。实际的大信号纹波电压为16.69 mV。使用线性表达式计算得到的大信号纹波电压，如[Hart 2011]所示，为14.9mV。而采用由我们模型推导出的公式(15)计算的结果为16.8mV，这再次验证了我们所提出模型的精度提升。

5.3. 同步升压转换器开环仿真

最后，为了验证所提出的模型在同步转换器上的有效性，使用表I中给出的元件对图10(b)中的同步升压转换器进行仿真。图15展示了所提出模型与晶体管级仿真结果的对比，表II总结了相关数据。可以看出，结果的精度非常高，同时仿真时间显著减少。

表I. 示例电路的元件值
升压转换器
L: 300μH
C: 1μF
rL: 50mΩ
rC（等效串联电阻）: 50mΩ

表II. 各种示例电路的仿真结果
转换器	参数	晶体管级	传统平均模型	所提出的增强型模型
开环升压	仿真时间	652s	32s	48s
	加速比	-	20X	13X
	误差/差异	-	30.60%	0.60%
闭环降压	仿真时间	1654秒	47s	55s
	加速比	-	35X	30X
	误差/差异	-	5.00%	0.3%
同步开环升压	仿真时间	667s	-	48s
	加速比	-	-	14X
	误差/差异	-	-	0.20%

6. 结论

我们提出了一种用于PWM DC‐DC转换器建模的增强型电路平均技术。该增强模型能够准确考虑电路中存在的非理想特性，从而在保持电路平均法计算成本优势的同时，提高了数值精度。本文还提出了增强的等效电路模型，用于确定连续导通模式（CCM）和断续导通模式（DCM）下的大信号与小信号特性。所获得的仿真结果验证了所提模型的有效性和精度。