超临界CO2循环PCHE设计与动态建模

超临界二氧化碳布雷顿循环印刷电路换热器的设计与动态建模

摘要

由于印刷电路热交换器的独特几何结构和流体力学特性以及超临界二氧化碳物性的快速变化，对印刷电路热交换器进行有效的设计与评级是其在超临界二氧化碳动力循环中应用的基本要求。在本研究中，已在Aspen Custom Modeler中为用于印刷电路热交换器布雷顿动力循环的印刷电路热交换器开发了一维设计与动态模型。设计模型通过最小化金属质量来确定最优几何参数。动态模型用于预测瞬态行为，并可轻松集成到在Aspen Plus Dynamics中开发的系统级模型中，以进行循环性能评估。在这些模型中，传热系数和摩擦系数是使用知名印刷电路热交换器制造商Heatric报告的数据计算得出的。这两个模型均通过海军核实验室运行的100千瓦级设施中使用的小型换热器数据进行了验证，然后应用于设计并模拟美国能源部关注的10兆瓦级超临界二氧化碳间接再压缩闭式布雷顿循环中的低温和高温回热器。所设计的印刷电路热交换器的设计与动态响应与传统管壳式换热器及微管壳管式换热器在相同应用条件下进行了比较。仿真结果表明，由于印刷电路热交换器的金属质量小且传热系数高，相较于传统管壳式换热器具有快速动态响应。尽管所设计的PCHEs的金属质量略高于微管壳管式换热器，但由于其成熟的制造工艺以及丰富的实验室和工业运行经验，印刷电路热交换器仍是热量回收的有前景候选方案。

1. 引言

超临界二氧化碳（sCO2）是一种有前景的发电替代工质，因其在高温[1,3]下运行时具有实现高效率和高功率密度[1,2]的潜力。Ahn等人[1]回顾了公开文献[1]中提出的多种sCO2动力循环构型。在各种配置中，间接超临界二氧化碳再压缩闭式布雷顿循环（RCBC）近期引起了关注，且开发一个10兆瓦电的超临界二氧化碳再压缩闭式布雷顿循环（sCO₂ RCBC）示范电厂是能源部在其超临界转化电能计划（STEP）项目下资助的重点。与典型的基于蒸汽的朗肯动力循环不同，整个超临界二氧化碳布雷顿循环通常在二氧化碳临界点以上运行。此外，超临界二氧化碳循环的压力比远小于蒸汽循环，因为最低压力略高于CO2的临界压力，而最大压力则受到关键设备、管道和测量系统的资本成本及机械设计的限制[1]。Dyreby等人[6]和Zitney等人[7]的研究表明，sCO2涡轮出口温度仍然较高，热侧涡轮出口流体与冷侧压缩入口流体之间的热量回收对sCO2布雷顿循环的整体效率、性能和动态行为至关重要。在最优设计的sCO2布雷顿循环中，回热器中的换热量预计远大于净功率输出，甚至大于热量输入[7,8]。例如，在一个10兆瓦电的sCO2再压缩闭式布雷顿循环电厂中，低温和高温回热器回收的总热量约为60兆瓦热功率，而主加热器所需的输入热量仅为21兆瓦热功率[7]。为了降低再压缩布雷顿循环资本成本和电厂占地面积，建议采用特殊设计的紧凑型换热器，作为优于传统壳管式换热器（CSTEs）的选择[9]。因此，此类回热器的有效选型、设计和运行对于sCO2布雷顿循环的成功示范和商业化至关重要。

印刷电路热交换器（PCHEs）和微管壳管式回热器（MSTEs）是两种具有前景的商用候选产品，可用作高效紧凑型热量回收换热器，正如Musgrove等人[10]、Le Pierres等人[11]以及Ngo等人[12]所建议的。最近，PCHEs已被应用于多个小型sCO2试验回路中，例如在海军核实验室[13]、桑迪亚国家实验室[14]和东京工业大学（TIT）[12,15,16]。此外，它们还被广泛采用用于下一代核反应堆，使用氦气、sCO2、钠和铅[17]等冷却介质。PCHEs是一种微通道换热器，由许多板片组成，每块板片上蚀刻有大量微波纹通道[18]。在PCHEs中，波纹通道由于其增强的传热性能而优于直通道，但代价是压降更高[12,19]。与CSTEs相比，PCHEs由于具有更高的单位体积传热面积，因而小得多且更轻，并且可以在较宽的条件下运行，同时保持合理的压降[20]。

需要注意的是，公开文献中已有若干针对紧凑型换热器设计的优化研究，这些研究主要关注优化策略，如序列二次规划（SQP）[21,22]和遗传算法[23]。这些研究还讨论了选择目标函数和约束条件的重要性，并分析了它们对换热器设计的影响[23,24]。然而，这些研究通常并未采用适用于超临界流体的热工水力关联式。此外，这些换热器模型不是动态的，且不易融入能够与其他设备模型连接的系统级稳态或动态建模环境。需要注意的是，换热器优化不仅是一个设备级问题，也是一个系统级问题[8,9]。设计温差和最大允许压降的选择不仅影响换热器的尺寸，还影响循环效率[9]和经济性能[8,25–29]。因此，使用一种便于在系统级建模环境中直接应用的建模平台（例如Aspen Custom Modeler (ACM)）来开发换热器设计非常重要，该平台可分别用于Aspen Plus和Aspen Plus Dynamics中的稳态或动态循环模拟。

为了开发最优控制策略并实现高效的伺服与抗干扰特性[30]，研究回热器的瞬态行为非常重要，因为由于其高热负荷，它会显著影响sCO2布雷顿循环的效率和负荷跟随特性。然而，目前仅开展了少数基于紧凑型换热器高保真模型的sCO2布雷顿循环系统级动态研究[31]。Luu等人开发的动态模型中，回热器是通过Dymola空调库[32]中已有的基本管道模型进行模拟的。Zitney和Liese的初步研究中，回热器在Aspen Plus Dynamics中被建模为CSTEs，并在Aspen Exchanger Design and Rating[7]中进行设计。Casella和Colonna使用Modelica开发了太阳能sCO2布雷顿循环的动态模型，其中设备模型主要取自ThermoPower库[33]，该库主要用于传统蒸汽动力循环。Simoes等人开发了基于偏微分方程(PDE)的gPROMS双管换热器动态模型2，用于超临界流体萃取过程中预热sCO2流体，但其中的气相热量平衡方程可能不适用于RCBC循环中因物性快速变化而导致的可压缩sCO[34]流动。

由于印刷电路板换热器(PCHE)结构的独特性以及CO2在超临界区域物性的显著变化，商用换热器设计和评级软件包对于sCO2布雷顿循环[23,35]并不准确。大多数精确的PCHE建模研究都是使用商业计算流体力学(CFD)软件（如FLUENT和COMSOL Multiphysics）进行的，这类方法通常计算成本高，不适合用于系统级设计或动态研究[7,19,31]。因此，一种常用的建模方法是开发简化的一维(1D)换热器模型[35,36]，其中努塞尔数和摩擦系数的相关性通过强制对流内流的经典经验方程进行估算，或者基于CFD仿真或实验数据生成新的热工水力方程。在一维模型中，换热器可被离散为若干相同长度[31,36]或相同热负荷[35]的段。后者更适合于设计阶段，而前者更适用于动态建模[9]。

国家能源技术实验室（NETL）的研究人员开发了一种用于在超临界二氧化碳循环中设计MSTEs的优化方法[9]。在该研究中，基于一维偏微分方程的MSTE模型在ACM环境中建立，并沿轴向进行离散化处理，采用在直管中针对超临界流体验证过的热工水力关联式进行设计，并利用序列二次规划算法对五个不同的目标函数（最小化金属质量、热滞留时间、总体积、传热面积，或最大化紧凑度）进行优化，这些目标函数与资本成本和动态性能相关。除了最大化紧凑度的情况外，无论选择哪个目标函数，结果均指向同一组最优几何设计[9]。如果能够获得适用于印刷电路热交换器的合适热工水力关联式，则此处也可采用类似方法对PCHEs进行优化设计。

一些研究已针对印刷电路热交换器（PCHE）在多种应用中的设计、模拟和运行展开。扎达等人提供了超临界二氧化碳（sCO2）动力循环中印刷电路热交换器的初步换热器尺寸确定和资本成本估算循环[8]。Le Pierres等人[11]和Ngo等人[12]研究了印刷电路热交换器的热工水力行为及其机械设计问题的影响。金和卢[37]使用FLUENT开发了用于高温气冷反应堆中间换热器的三维（3D）数值模型，并提出了根据层流区域中的雷诺数和通道设计参数预测摩擦系数和传热系数的关联式。然而，这可能不适用于在充分发展湍流区域[37,38]中运行的超临界二氧化碳布雷顿循环中的印刷电路热交换器。梅什拉姆等人开发了一维热模型，并使用了基于FLUENT CFD仿真得到的努塞尔数和摩擦系数关联式，其中印刷电路热交换器在湍流区域[19]内以超临界二氧化碳流体运行。盖泽利乌斯通过假设直通道开发了印刷电路板式换热器模型，其热工水力关联式由CFD仿真[39]生成。在卡斯滕斯开发的全厂范围超临界二氧化碳布雷顿循环模型[31]中，具有直通道的印刷电路热交换器沿轴向方向离散化，并通过一系列代数方程进行建模，其中传热系数和摩擦系数采用传统的充分发展的层流或湍流内流关联式（如格尼林斯基关联式和科尔布鲁克‐怀特方程）计算。在卡斯滕斯的模型[31]中，动量守恒被视为准静态过程，因此无法准确捕捉印刷电路热交换器在运行条件快速变化时的动态行为。

总之，热量回收对于提高超临界二氧化碳布雷顿循环的经济性和性能至关重要，而基于印刷电路热交换器的回热器由于其商业成熟度、坚固的机械设计和紧凑的占地面积，成为最合适的候选方案之一。因此，开发可用于设计和动态研究的可靠印刷电路热交换器模型至关重要。理想的印刷电路板式换热器模型应能够表征稳态性能以及超临界二氧化碳电厂在启动、停机和变负荷运行期间的动态行为，同时在集成到整个循环的系统级模型中时仍具有计算上可处理性。然而，现有的印刷电路热交换器模型要么并非专门为超临界流体开发，要么在系统级仿真中不具备计算上可处理性，要么未经过优化设计，要么缺乏稳态或动态实验数据的验证，尤其是在超临界二氧化碳动力循环应用中。此外，在公开文献中尚未使用严格模型对适用于超临界二氧化碳动力循环的不同类型换热器进行过比较。

基于上述动机，开发了用于超临界二氧化碳（sCO2）布雷顿循环中运行的印刷电路热交换器（PCHE）的一维稳态和动态模型。这两个模型均通过与海军核实验室建造的集成系统测试（IST）设施所获得的实验数据进行验证。该设施是一个小型（100 kWe）简单回热布雷顿循环（SRBC），采用相同的运行条件和几何结构设计[13]。具体而言，本研究的贡献可总结如下：（1）基于公开文献中的数据，回归得到了适用于波纹通道PCHE及sCO2工作流体的热工水力关联式；（2）建立并验证了一维PCHE模型，该模型在保证严谨性的同时具有计算上可处理的特点，适用于全厂范围模拟；（3）采用序列二次规划算法对代表当前正在建设的美国能源部资助的STEP项目示范电厂规模的10兆瓦电sCO2再压缩闭式布雷顿循环（RCBC）的回热器设计进行了优化；（4）分析了关键设计参数对PCHE稳态性能的影响；（5）利用所开发的动态模型研究了PCHE的瞬态行为；（6）比较了在相同再压缩布雷顿循环应用和电厂规模下，最优设计的PCHE与另外两种竞争方案——紧凑型壳管式换热器（CSTEs）和MSTE——之间的关键设计措施和动态行为。

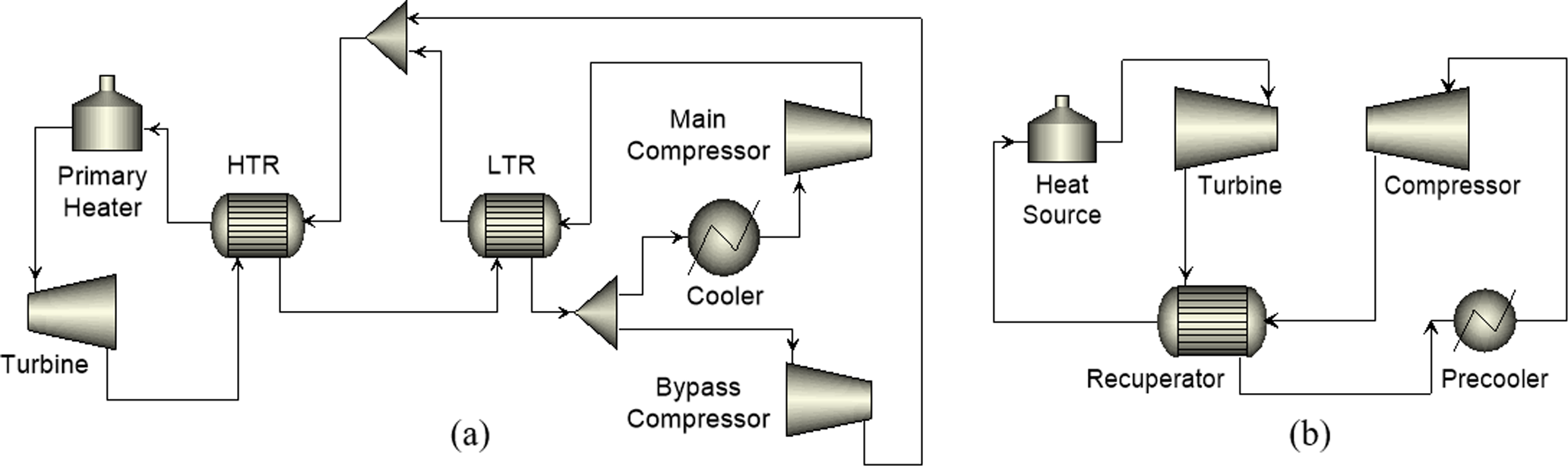
2. sCO2布雷顿循环的构型

已对多种sCO2布雷顿动力循环布局进行了研究在公开文献中[1,41,42]。在这些被建议的布局中，如图1(b)所示的简单回热布雷顿循环（SRBC）布局是最简单的之一，常被考虑用于实验室规模的测试设施，包括海军核实验室建造的100千瓦电IST设施[13]。其他更先进的布局通常包含蒸汽循环中常用的几种设计，例如中间冷却、再热和分流等。[1]如图1(a)所示的再压缩布雷顿循环（RCBC）布局是一种典型的带分流的sCO2动力循环，已被美国能源部STEP计划资助的10兆瓦电级示范规模sCO2布雷顿循环电厂项目所采用[4,5,7]。在RCBC布局中，使用了两个回热器：高温回热器（HTR）和低温回热器（LTR），用于热量回收。来自LTR的一部分低压流体不经过冷却，直接送往旁路压缩机，并在进入HTR之前与主高压流体混合。RCBC布局避免了由于sCO2在高压侧与低压侧之间比热差异显著而产生的温度夹点，从而增加了回收热量的量以及整体循环效率[1]。

本研究利用实验室规模IST设施中回热器在宽范围工况下的稳态和动态数据以及设计几何参数（图1(b)）[13]来验证印刷电路板式换热器模型。然后，针对中试规模sCO2 STEP电站（图1(a)）中的高温回热器和低温回热器进行印刷电路热交换器的最优尺寸设计，以研究更先进且更大规模的sCO2循环中回热器的动态行为。表1给出了对应于STEP和IST设施循环在设计和非设计工况下回热器的入口条件。对于IST设施，回热器的入口条件由试验回路实测获得[13]。对于STEP设施，高温回热器和低温回热器的入口条件是基于国家能源技术实验室使用Aspen Plus开发的系统级工艺模型估算得到的[4,7]。

再压缩闭式布雷顿循环 ( 10兆瓦电STEP电站 ) 和 ( b ) 简单回热布雷顿循环 ( 100千瓦电IST设施 ))

3. 印刷电路热交换器的优化设计与动态建模

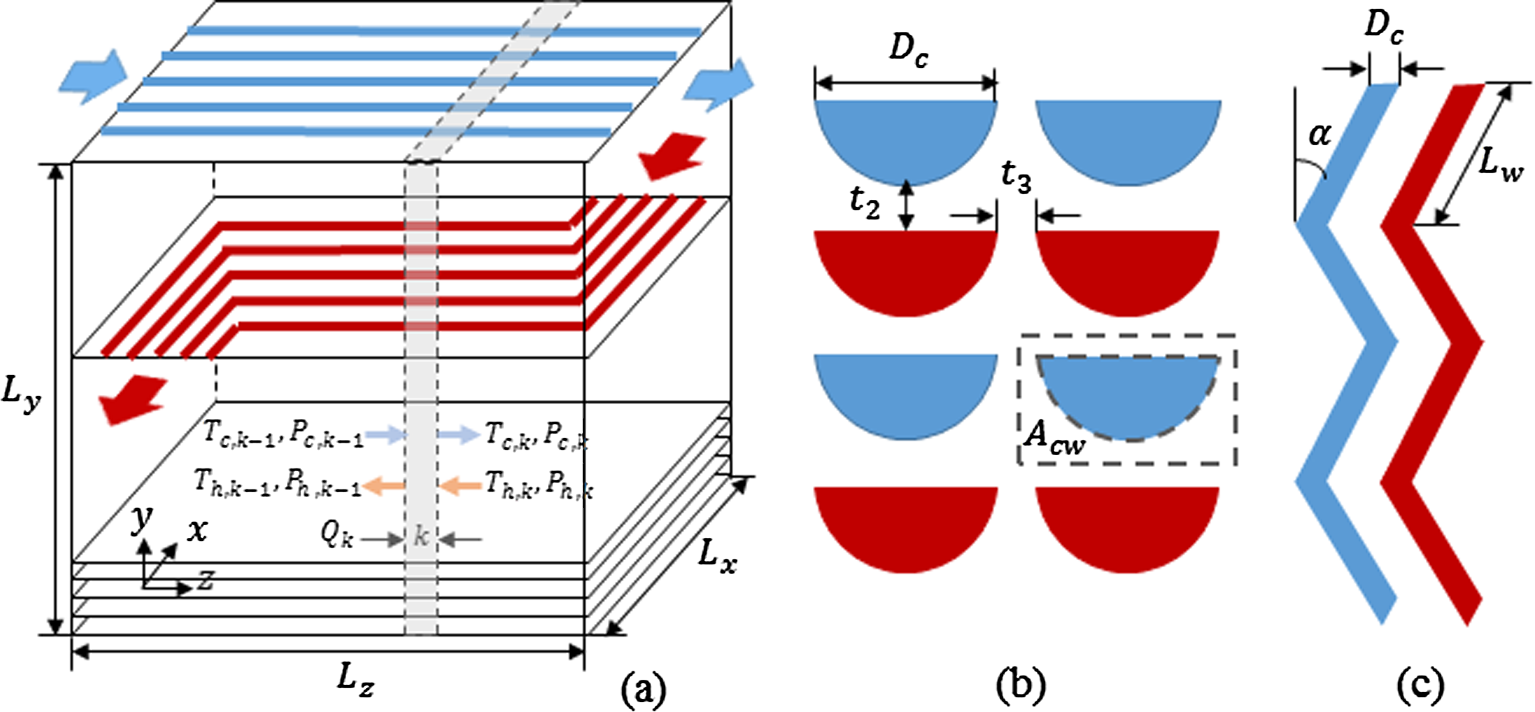
在本研究中，选择印刷电路热交换器用于sCO2布雷顿循环中的余热回收，针对该系统已在ACM中建立了简单的[10–12],一维模型，以进行优化设计和动态仿真，其基于以下假设：（1）充分发展湍流[15,31], （2）理想逆流，且忽略进出口效应[13,43], （3）轴向扩散效应可忽略不计；（4）沿通道轴线的一维温度分布；（5）热损失可忽略不计；以及（6）每个通道入口处的温度、压力和流速均匀[37,43]。几何结构和优化设计模型在第3.1节和第3.2节中描述，而动态模型中使用的可压缩sCO2流体的质量、热量和动量平衡方程在第3.3节中详细说明。物性模型和经验热工水力关联式在第3.4节中讨论。需要注意的是，上述模型涉及强非线性偏微分方程，因此应仔细选择ACM内置数值求解器中的参数以提高数值鲁棒性并确保模型稳定性。在本研究中，冷热流体和壁面的偏微分方程离散化方法分别选择为二阶向后有限差分（BFD2）和二阶向前有限差分（FFD2）。沿z方向图2(a)的节点数设置为100[9]。积分器采用变步长的隐式欧拉法[44]。

3.1. 印刷电路热交换器的几何结构

如图2(a)所示，印刷电路热交换器中带有蚀刻通道的热板和冷板通过扩散焊接交替排列并组装在一起[20,37]。在本研究关注的设计中，冷热流体主要呈逆流流动，由于集管布置的原因，在进出口处存在有限的横向流动[11,20]。除了逆流外，板片还可根据需要定制为多程逆流或多程逆交混流[20]。与板片排列相关的几何参数包括板片数量（Np）、每板通道数（Nc）以及热板与冷板数量之比（Rp）。核心尺寸由Lx×Ly×Lz表征。Rp在大多数情况下通常设为1，但在某些特殊情况下也可设为2。例如，在TIT给出的PCHE设计中，超临界二氧化碳循环试验回路2试验回路[12,15]中考虑了每块冷板对应两块热板（Rp=2）。佐胡里还建议，在热侧使用更多通道有助于实现最大传热[45]。

如图2(b)所示，蚀刻通道的横截面大多为半圆形，通道宽度（Dc）在0.2 mm到5 mm之间变化[11,20]。壁厚（t2）和脊宽（t3）可根据运行条件、通道宽度、所选材料的设计应力和腐蚀余量，依据ASME 13‐9规范确定[9,11]。如图2(c)所示，锯齿形图案通常用于印刷电路热交换器的设计中[11,12,37]。除了Dc，波角（α）和波长宽比（Lw/Dc）是另外两个重要的流道设计参数。例如，增大α将增加印刷电路热交换器的整体体积比表面积和传热系数[15,39],但也会增加压降，这是不希望的[11]。α通常在25–40°之间，但可从5°变化到45°[37–39],而在典型的印刷电路热交换器中，该值通常在4到7之间[39]。本研究仅评估了两种流道设计，即低角度设计和高角度设计，所采用的热工水力关联式是基于公开文献中的实验数据开发的[11]。实际流道长度（Lc）与印刷电路热交换器芯体长度（Lz）相关，如公式(1)所示。本研究中，通道宽度固定为2毫米，与Heatric的研究类似[39]。

$$ L_c = \frac{L_z}{\cos(\alpha)} $$ (1)

3.2. 设计与优化

PCHE的稳态设计模型与本文作者开发的MSTE模型类似[9]。由于sCO2物性的快速变化，回热器沿z方向被离散为多个子换热器，如图2(a)[9,35]所示。每个子换热器分配相同的热负荷（Qk），其中Q为根据总体能量平衡计算的总热负荷，给定设计温差（Td）和入口流动条件（Thin, Cin, Pin, Phin, Fmh, Fmc）[9]。每个子换热器的进出口温度通过局部热平衡计算，如公式(2)所示。每个子换热器的热导（UAk）采用对数平均温差（LMTD）法计算，如公式(3)所示。每个子换热器的总传热系数（Uk）由公式(4)计算，假设无污垢热阻，因为CO2纯度较高[14,46]。在公式(4)中，Uk基于冷侧传热面积（Ak）计算，见公式(5)；te为公式(6)中定义的等效壁厚；hh和hc分别为热侧和冷侧的传热系数；kw为金属壁的导热系数；Lc,k为每个子换热器的通道长度。对于每个子换热器（k），sCO2流体和金属壁的物性在算术平均温度（0.5(Tk-1 + Tk)）和压力（0.5(Pk-1 + Pk)）下进行评估[36,47]。每个子换热器中的压降（|ΔPk|）由公式(7)计算，其中fk、ρk、vk分别表示达西摩擦系数、密度和流速；Dh为半圆形通道的水力直径，见公式(8)，定义为4×流通截面积/润湿周长。

$$ Q_k = \frac{Q}{N} $$

$$ T_{c,out,k} = T_{c,in} + \frac{Q_k}{F_{m,c} \cdot C_{p,c}} $$
$$ T_{h,out,k} = T_{h,in} - \frac{Q_k}{F_{m,h} \cdot C_{p,h}} $$ (2)

$$ UA_k = \frac{Q_k}{LMTD_k} = \frac{Q_k}{\frac{(T_{h,k}-T_{c,k})-(T_{h,k-1}-T_{c,k-1})}{\ln((T_{h,k}-T_{c,k})/(T_{h,k-1}-T_{c,k-1}))}} $$ (3)

$$ \frac{1}{U_k} = \frac{1}{h_{c,k}} + \frac{t_e}{k_w} + \frac{1}{h_{h,k} \cdot R_p} $$ (4)

$$ A_k = \left( \frac{1}{R_p} + 1 \right) \cdot N_p \cdot N_c \cdot \pi \cdot D_c \cdot L_{c,k} $$ (5)

$$ t_e = \frac{t_2 + t_3}{2} + \frac{\pi \cdot D_c \cdot t_2 \cdot t_3}{8} $$ (6)

$$ |\Delta P_k| = \frac{f_k \cdot L_{c,k} \cdot \rho_k \cdot v_k^2}{2 \cdot D_h} $$ (7)

$$ D_h = \frac{D_c}{2} + \frac{\pi \cdot D_c}{4} $$ (8)

本研究中，利用ACM内置优化器HYPSQP对10 MWe再压缩布雷顿循环电站中的高温回热器（HTR）和低温回热器（LTR）进行最优设计[9,44]，最小温差为10 °C[7]，最大允许压降（Pmax）为1.4 巴。根据设计工况，选用SS316（ρ=7990 千克/m³）作为结构材料[9,13]。目标是最小化印刷电路热交换器的总金属质量（MHX），这是紧凑型换热器的关键特性之一，与其成本和动态性能密切相关[9,36]。在给定流道设计（α）和板片排列（Rp）的情况下，决策变量和设计约束条件汇总于表2。根据知名印刷电路热交换器制造商Heatric的说法，目前可提供的最大板片尺寸为600×1500 mm[20]。每个印刷电路热交换器模块的高度（Ly）——即通过扩散焊接连接在一起的一组板片——受板片焊接设备限制，不得超过1米[48]；然而，若最终设计所需高度（Ly）超过其上限，则可通过连接多个模块组成单个单元的最终换热器核心，其重量范围为1千克至60吨[20]。若最终设计所需的宽度（Lx）或长度（Lz）超过其上限，可考虑采用并联或串联的多个单元。由于运输要求，每个印刷电路热交换器单元的核心尺寸限制为2×3×2 m[9,49]。需要注意的是，ACM内置优化器仅能处理连续优化变量，无法求解混合整数非线性优化问题。因此，在优化阶段，将离散变量Np和Nc视为连续变量处理，随后取其最接近的整数值用于最终设计。

3.3. 动态建模

在ACM中开发了一种一维动态模型，用于捕捉sCO2布雷顿循环回收过程中印刷电路热交换器的动态行为，其中长度方向（见图3）被划分为相同长度的段（Lz/N）[31,36]。瞬态传热方程表示为公式（9）、（11）和（13），边界条件由公式（10）、（12）和（14）给出。在公式（9）–（14）中，符号ρ、U、H、Cp、k、G、h、T分别表示冷侧（c）和热侧（h）sCO2流体以及金属壁（w）的密度、摩尔内能、摩尔焓、比热、导热系数、总摩尔流量、传热系数和温度。D和Acw分别为每个通道的横截面积和周长。Ncp和Nhp分别为冷侧和热侧的通道数量。公式（13）中每通道金属壁的横截面积（Acw）通过公式（15c）计算，如图2（b）所示。

$$ \rho_c \cdot C_{p,c} \cdot \frac{\partial T_c}{\partial t} + G_c \cdot \frac{\partial H_c}{\partial z} = \frac{1}{2} \cdot N_{cp} \cdot h_c \cdot D \cdot (T_w - T_c) $$ (9)
$$ T_c(z=0) = T_{c,in} $$ (10)
$$ \rho_h \cdot C_{p,h} \cdot \frac{\partial T_h}{\partial t} + G_h \cdot \frac{\partial H_h}{\partial z} = \frac{1}{2} \cdot N_{hp} \cdot h_h \cdot D \cdot (T_w - T_h) $$ (11)
$$ T_h(z=L_z) = T_{h,in} $$ (12)
$$ \rho_w \cdot C_{p,w} \cdot \frac{\partial T_w}{\partial t} = k_w \cdot \frac{\partial^2 T_w}{\partial z^2} + \frac{1}{2} \cdot \left( \frac{1}{R_p} + 1 \right) \cdot h_c \cdot D \cdot (T_c - T_w) + \frac{1}{2} \cdot \left(1 + R_p \right) \cdot h_h \cdot D \cdot (T_h - T_w) $$ (13)
$$ \frac{\partial T_w}{\partial z}(z=0) = \frac{\partial T_w}{\partial z}(z=L_z) = 0 $$ (14)

$$ N_{cp} = \left( \frac{1}{R_p} + 1 \right) \cdot N_p \cdot N_c $$ (15a)
$$ N_{hp} = \left(1 + R_p \right) \cdot N_p \cdot N_c $$ (15b)
$$ A_{cw} = \frac{\pi \cdot D_c \cdot t_2}{2} + \frac{\pi \cdot D_c \cdot t_3}{2} + \pi \cdot D_c \cdot t_2 \cdot t_3 $$ (15c)

式（16）和（17）给出了sCO2流体的质量和动量平衡，其中符号v、P和f分别表示流速、压力和达西摩擦系数，Dh为通过式（8）计算得到的热侧和冷侧通道的水力直径。流体的入口压力和流速被指定为边界条件。热侧和冷流体的质量流量由式（18）和（19）给出。

$$ \frac{\partial v}{\partial t} + \frac{\partial v}{\partial z} = 0 $$ (16)
$$ \frac{\partial v}{\partial t} = -\frac{1}{\rho} \cdot \frac{dP}{dz} - \frac{f \cdot v^2}{2 \cdot D_h} $$ (17)
$$ F_{m,h} = \frac{1}{8} \cdot \pi \cdot \left(1 + R_p \right) \cdot N_p \cdot N_c \cdot D_c^2 \cdot \rho_h \cdot v_h $$ (18)
$$ F_{m,c} = \frac{1}{8} \cdot \pi \cdot \left( \frac{1}{R_p} + 1 \right) \cdot N_p \cdot N_c \cdot D_c^2 \cdot \rho_c \cdot v_c $$ (19)

3.4. 物性模型与热工水力关联式

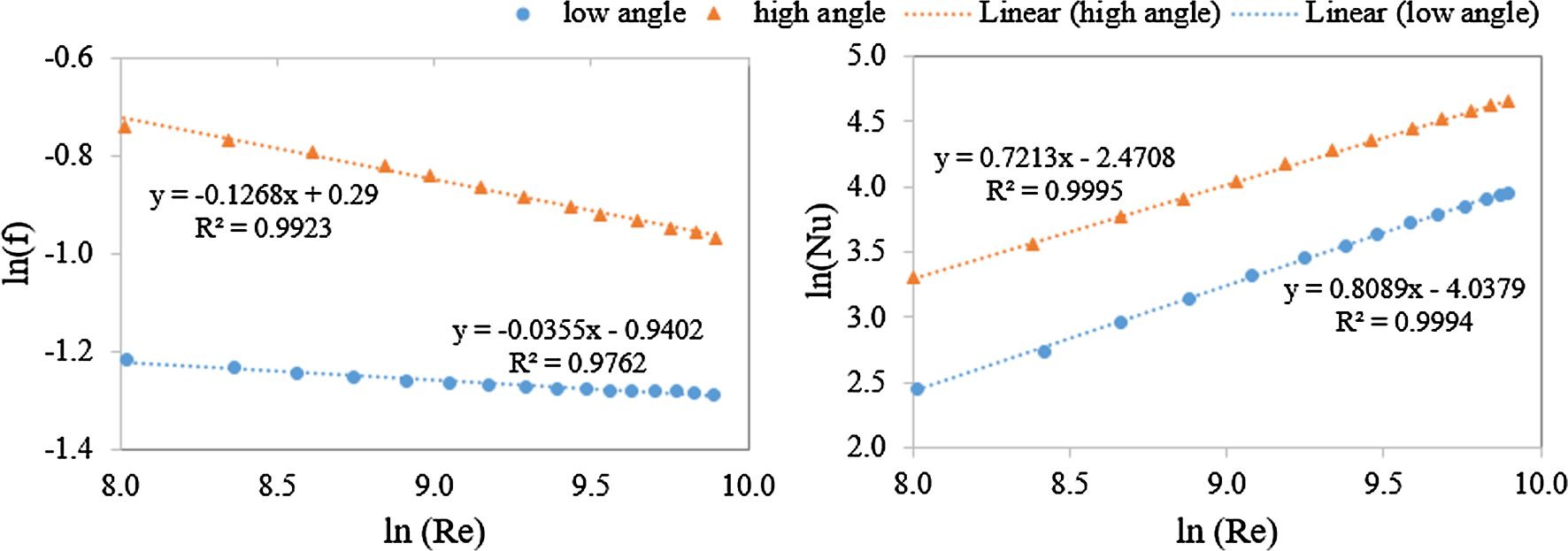
在本研究中，使用NIST REFPROP基于亥姆霍兹自由能2评估sCO2的流体性质。需要注意的是，CO2的大多数热和输运性质，例如摩尔焓（H）、黏度（µ）、导热系数（k）和密度（ρ），可通过ACM内置的物性调用[9]进行计算，但尚无用于计算内能（U）的物性调用功能。因此，在本研究中，通过热力学定义计算U=H-PV，其中V为摩尔体积。对于材料SS316，导热系数（kw）和比热（Cpw）的温度相关关联式由公式(20)和(21)给出，其中kw单位为W/m/°C；Cpw单位为kJ/kg/°C；Tw单位为°C[9]。如图3所示，小角度通道和大角度通道的热液压性能分别由公式(22)和(23)表征，这些是基于Heatric提供的数据回归得到的经验关联式，雷诺数范围为3000至20,600[11]。此处，努塞尔数和雷诺数采用公式(8)给出的水力直径进行计算。

$$ k_w = 13.189 + 0.0153 \cdot T_w $$ (20)
$$ C_{pw} = 10^{-3} \cdot (463.54 + 0.3119 \cdot T_w - 0.0002 \cdot T_w^2) $$ (21)
$$ Nu = 0.0176 \cdot Re^{0.809} \cdot Pr^{1/3} $$ (22a)
$$ f = 0.3905 \cdot Re^{-0.0355} $$ (22b)
$$ Nu = 0.0845 \cdot Re^{0.721} \cdot Pr^{1/3} $$ (23a)
$$ f = 1.336 \cdot Re^{-0.1268} $$ (23b)

4. 结果与讨论

本研究中，回热器针对兆瓦级10 MWe sCO2再生式二氧化碳布雷顿循环电站进行了优化设计和仿真。在第4.1节中，通过与100千瓦电IST设施的数据进行比较，验证了稳态（设计）和动态模型[13]。针对10兆瓦应用的更大的印刷电路热交换器的优化设计详见第4.2节。在第4.3节中，通过引入入口条件的阶跃变化以及快速和慢坡道来研究印刷电路热交换器。在第4.4节中，对印刷电路热交换器在sCO2循环中用于热量回收的设计与性能进行了与MSTE和紧凑型壳管式换热器的比较。

4.1. 模型验证

在本节中，通过与海军核实验室[13]运行的IST设施（图1(b)）的数据进行比较，对PCHEs的稳态（设计）和动态模型进行了验证。表3中列出了以SS316为建造材料的PCHE，其尺寸(Lx,Ly,Lz)设置为与IST设施中使用的回热器相同，而其他几何参数（如Np和Nc）则根据海军核实验室提供的有限几何数据计算得出。需要注意的是，ACM采用基于方程的模拟方法。因此，如果将N设置为自由变量并固定几何参数，则第3.2节中讨论的设计模型也可用于换热器的额定计算[44]。

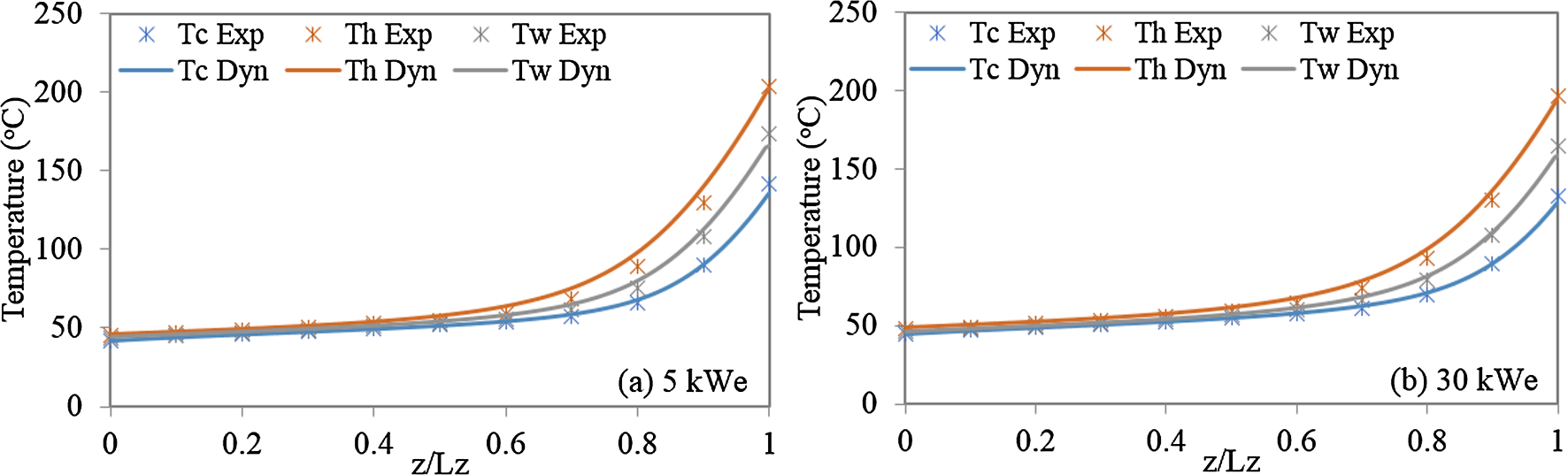
表4总结了在设计工况（净功率=100 kWe）和两个变工况（净功率=30 kWe和5 kWe）下的稳态实验数据（Exp），以及设计（Des）模型和动态（Dyn）模型的仿真结果[13]。观察到Des与Dyn模型之间存在微小差异，这是由于这两个模型所采用的空间离散化方法不同所致，如第3.2和3.3节所述。通过增加离散化节点可以减小该差异，但代价是计算时间增加。在图4中，将两种变工况下的温度分布与克莱蒙托尼等人报告的数据进行了比较[13]。可以看出，两个模型均能合理预测印刷电路热交换器在宽范围运行条件下的性能和温度分布。模型与实验数据在压降方面的差异约为0.2巴，而在出口温度方面的差异（主要在冷侧）小于5°C，约为回热器两侧温度变化的6%。造成这一微小差异的可能原因包括焓模型的不准确性（估计约为2–4%）[50]、向环境的热损失估计不准确[16]，以及实验数据与模型之间热流体和冷流体压力可能存在不匹配，因为在克莱蒙托尼等人的研究中未提供变工况下的压力数据[13]。此外，尼基廷等人指出，冷侧和热侧热损失的不平衡会导致总热负荷的不平衡。他们还注意到，热损失的绝对值并不强烈依赖于雷诺数和总热负荷，因此随着设备规模的增大，由于热损失与总热负荷之比减小，这些差异有望进一步降低[16]。

在图5中，IST设施中两个变工况点之间启动过程的瞬态数据被用于验证本研究开发的动态模型[13]。需要注意的是，克莱蒙托尼等人报告的数据来自完整的sCO2循环测试，因此回热器的入口条件存在振荡现象[13]。在此对比中，模型中指定了入口条件（即温度和流量），而出口条件则由模型计算得出。在ACM中添加了多个流程任务，以模拟启动过程中入口条件的变化，如图5(a)和(d)所示。如图5(b)和(c)所示，尽管模型预测的绝对值比实验结果低约5°C，与表4中的结果类似，但总体上瞬态数据的形状，特别是模拟的响应时间，与实验数据相似。可以看出，该动态模型能够成功捕捉印刷电路热交换器的动态行为。然而，观察到模型的瞬态行为相较于实验数据更为平滑，这可能是由于热流体和/或冷流体的入口压力存在差异所致。需要注意的是，温度偏差仅出现在变工况情况下，这是由于实验数据与模型之间的热侧和冷侧流体压力可能存在不匹配所致，因为压力数据在克莱蒙托尼等人的研究中未提供非设计工况下的数据。[13]实验数据来自一个简单循环装置，如图1（b）所示，其中系统压力在瞬态运行期间预计将发生轻微变化，从而影响动态响应的特性。

4.2. 10兆瓦电站中印刷电路热交换器的优化设计

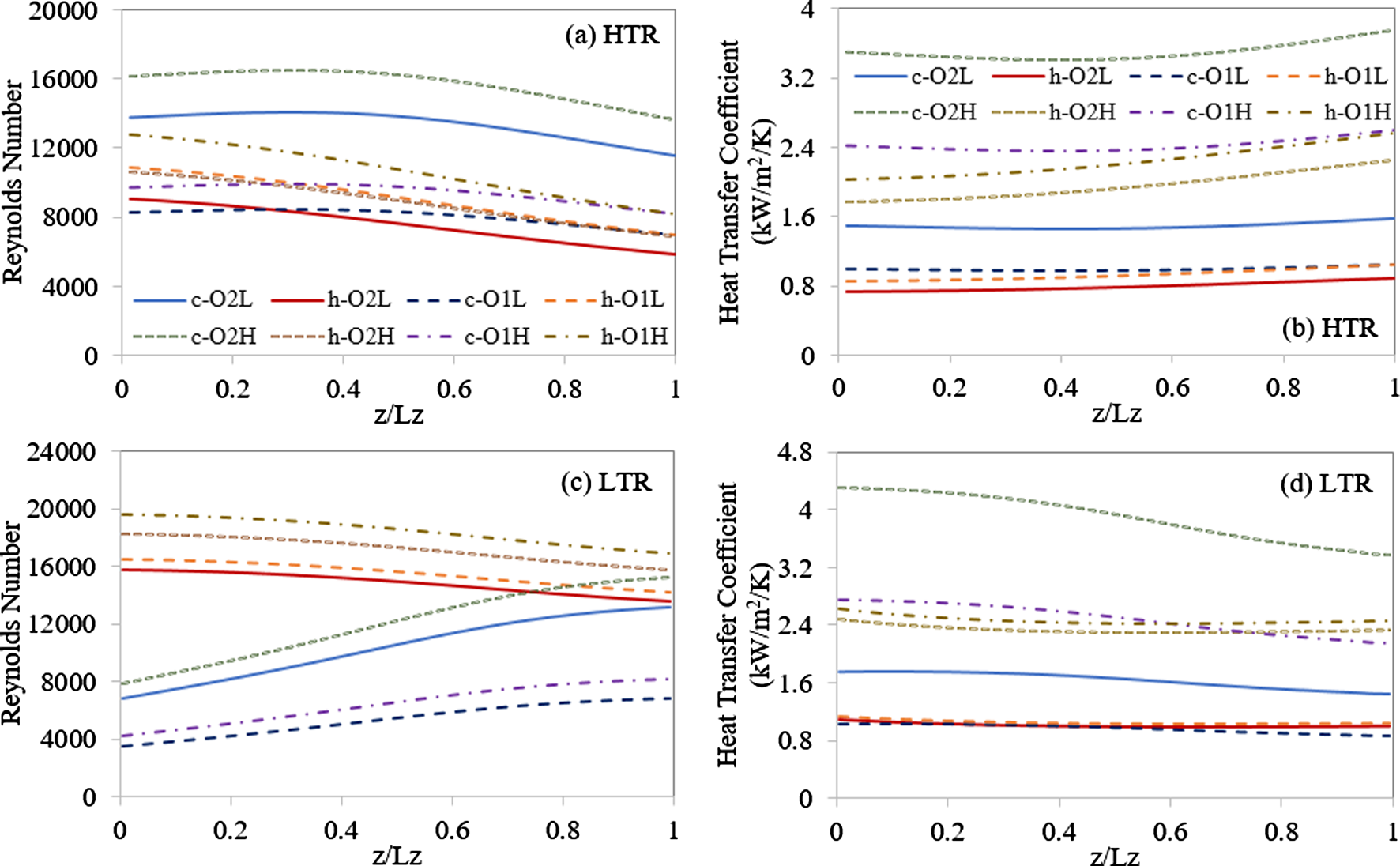
本节中，采用第3.2节所述模型对10 MWe sCO2再压缩布雷顿循环电站（图1(a)）中的HTR和LTR进行优化设计，所用运行条件汇总于表1，优化问题的表述总结于表2。表5列出了基准设计中回热器出口流道条件及热平衡情况。表6给出了通过序列二次规划算法生成的最优设计（O1L、O2L、O1H、O2H），这些设计针对不同结构（单层或双层热板）以及（低角度或高角度）通道的回热器，其雷诺数和传热系数分布见图6。设计方案名称中的字母O表示最优，数字1和2表示每块冷板堆叠的热板数量（单层或双层），L和H分别代表低角度和高角度通道。如第3.2节所述，由于当前制造方法对印刷电路热交换器板片尺寸的限制，大规模热量回收可能需要多组模块。表6中，P×S为并联和串联所需的模块数量；Lx、Ly和Lz分别为每个模块的宽度、高度和长度；MHX为所有模块的总金属质量。与TIT为sCO2应用设计的小型印刷电路板换热器相比，[16]我们采用小角度通道的设计总体传热系数（UHX）约低40%，而采用大角度通道的设计则约高30%。Le Pierres等人也报道了不同印刷电路热交换器流道设计之间的类似比较结果。此外，在10 MWe再压缩布雷顿循环电站中，采用O2H设计的高温回热器的金属质量大约仅为Schmitt等人在100 MWe再压缩布雷顿循环电站中优化的微通道回热器金属质量的九分之一，这表明该设计模型可适用于广泛的处理量范围[36]。

结果表明，与采用(O1L, O1H)的设计相比，采用(O2L, O2H)的设计在HTR和LTR中均具有更低的金属质量（MHX），而每块冷板使用两块热板的优势在LTR中更为显著。如表6所示，回热器的长度（Lz）受限于最大允许压降（Pmax），这与本文作者在先前研究中关于sCO2再生式二氧化碳布雷顿循环电站[9]中微管回热器优化设计所得出的结论相似。对于大型PCHE，所需的传热面积（AHX）以达到期望的Td或可通过增加总计通道数量Np×Nc来满足。然而，表6表明，在质量流量固定的情况下，通道数量（Np×Nc）的增加会降低流速，从而导致UHX减小并增加所需Lz值。在HTR中，冷侧和热侧的质量流量相近。如果考虑热侧与冷侧采用相同的板片数量和相同的流道设计，则由于温度较高且压力较低，热侧的体积流量通常更高，最终导致热侧压降较大并限制Lz。在LTR中，由于热侧的质量流量更高，如表1所示，这种情况更加严重。因此，在双热板设计与单热板设计之间，MHX的差异在低温回热器的尺寸大于高温回热器。通常情况下，本文提出的超临界二氧化碳布雷顿循环中，双热板设计显得更具竞争力。

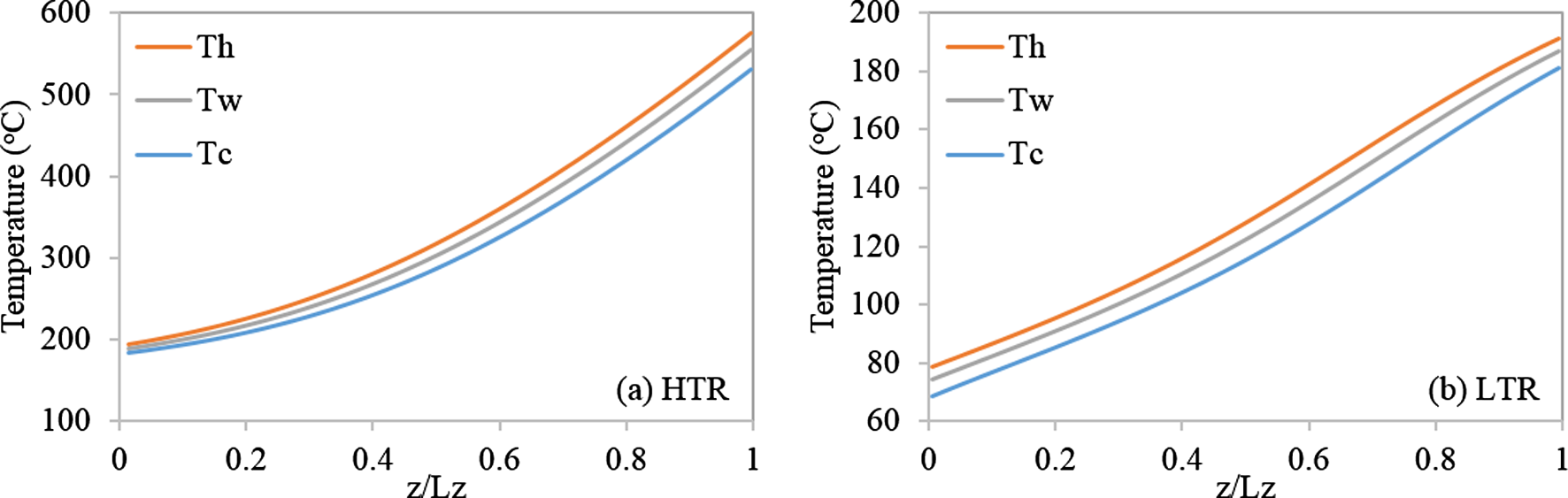
表6还表明，采用大角度通道的设计（O1H, O2H）可显著减少整体金属质量，而采用小角度通道的设计（O1L, O2L）紧凑性较差，且由于板尺寸的上限，需要多个并行流程。大角度通道设计更优的原因仅仅是其具有更高的传热速率，如图3（b）所示。因此，采用大角度通道的设计O2H具有最小的金属质量并被选为两个回热器的最终优化设计，其几何结构数据将在后续的动态模拟中使用。图7给出了10兆瓦电站在最终优化设计（O2）下高温回热器和低温回热器的温度分布。如图7所示，壁面温度曲线几乎位于冷流体和热流体温度曲线的中间位置。这表明热侧和冷侧的传热阻力相近[9]。

4.3. 印刷电路板式换热器的时间常数与动态特性

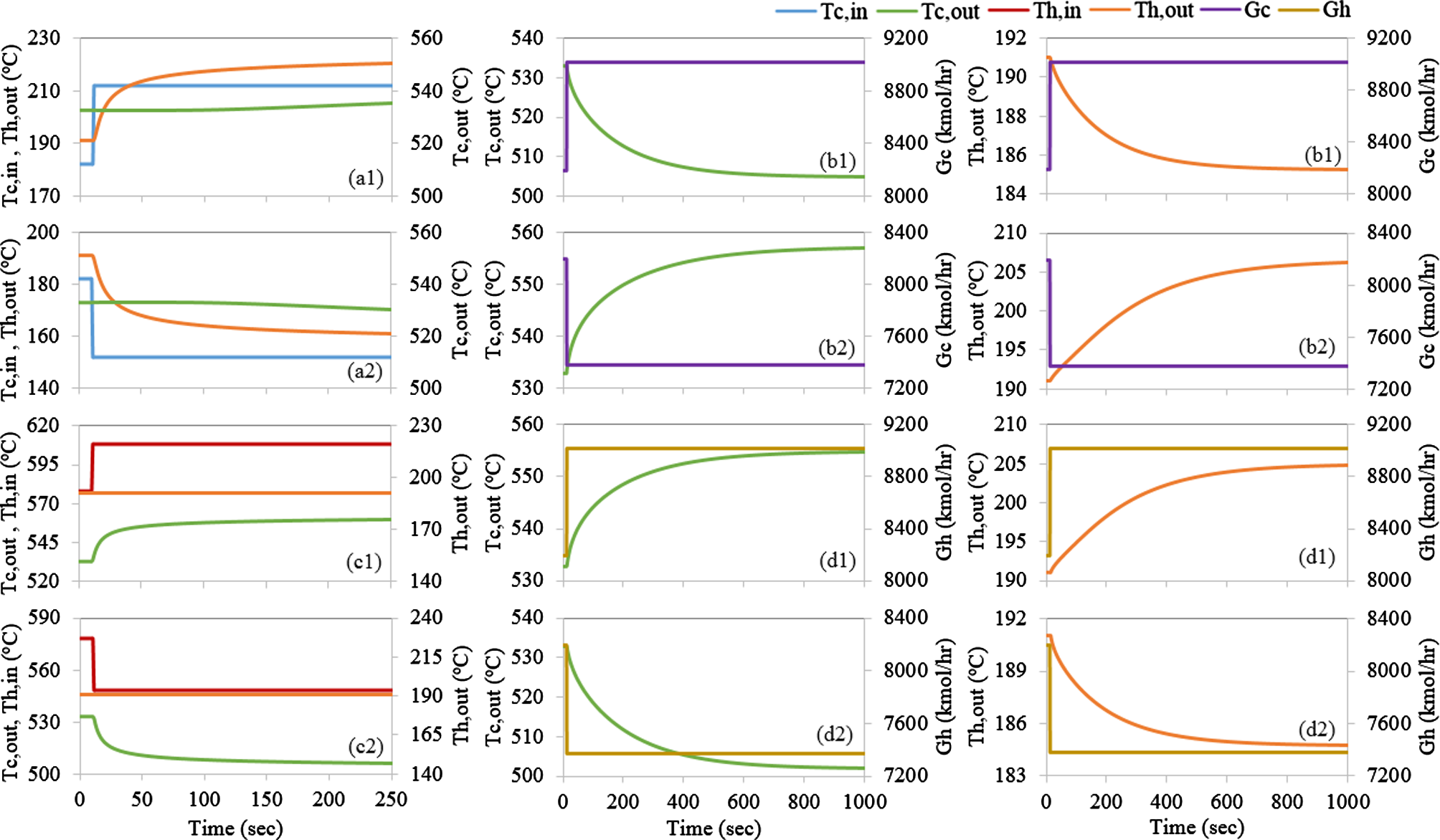
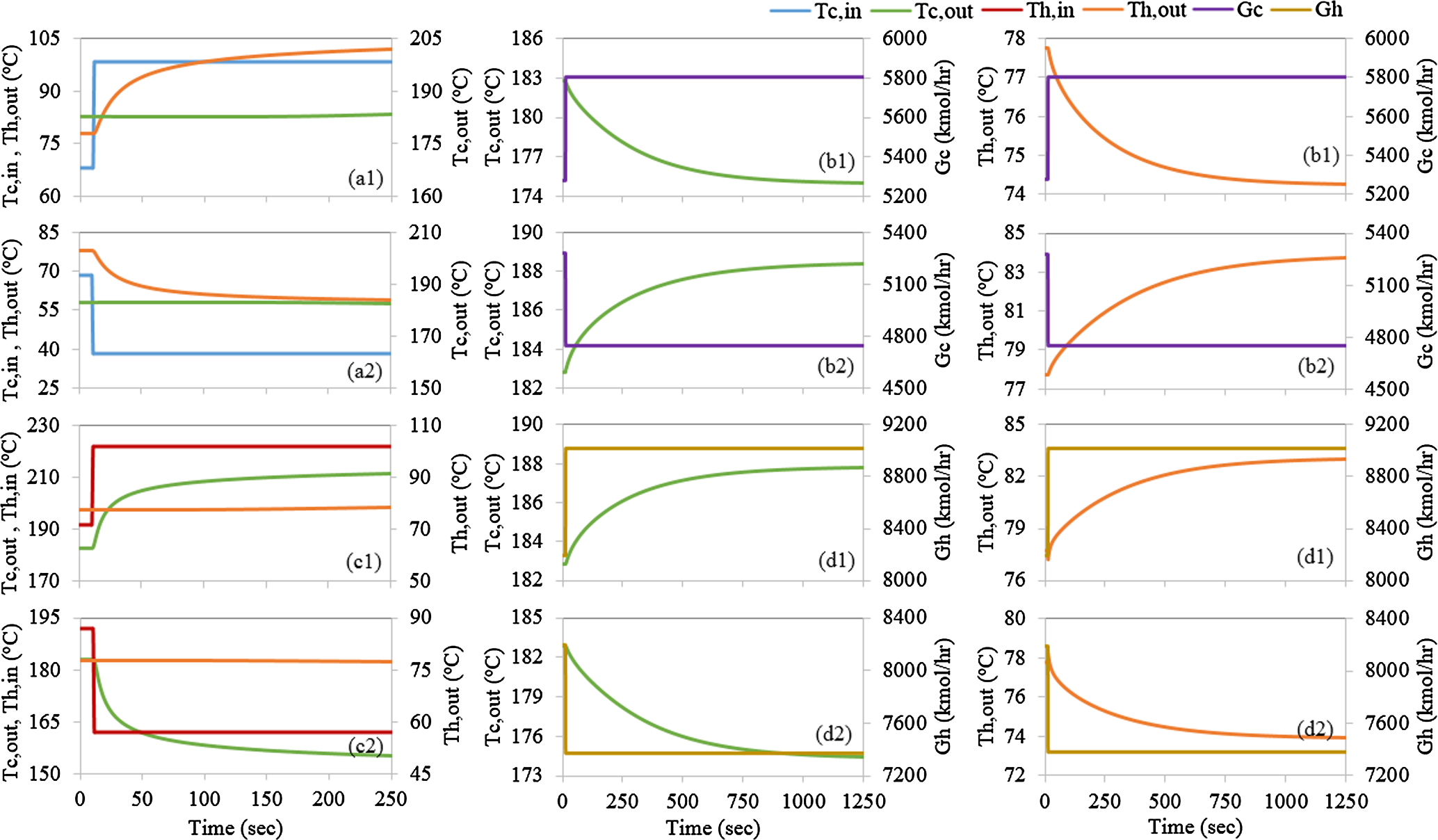
在第4.2节中获得的最终优化设计（O2H）的几何参数被指定用于两个回热器的动态模型中。稳态模型在设计工况下生成的结果被用作下文所述动态仿真的初始条件。为了评估10 MWe再压缩布雷顿循环电站（图1(a)）中高温回热器（图8）和低温回热器（图9）的时间常数，在冷侧入口温度处引入30°C的阶跃变化(图8(a)和9(a))以及热侧(图8(c)和9(c))，同时在冷侧入口流量(图8(b)和9(d))引入10%的变化。瞬态响应可通过时间常数(τ)来表征，该时间常数定义为系统响应在阶跃输入下达到其最终值所需的时间。表8表明，对于入口温度的阶跃变化，时间常数较小（约或小于15秒），而对于入口流量的阶跃变化，时间常数相对较大（约1或2分钟）。类似地，比较图(a)和(c)与图(b)和(d)，可以观察到回热器对温度变化的动态响应比对流量变化的动态响应更快，这可能是由于流量变化引起的热容滞量变化更为显著所致。

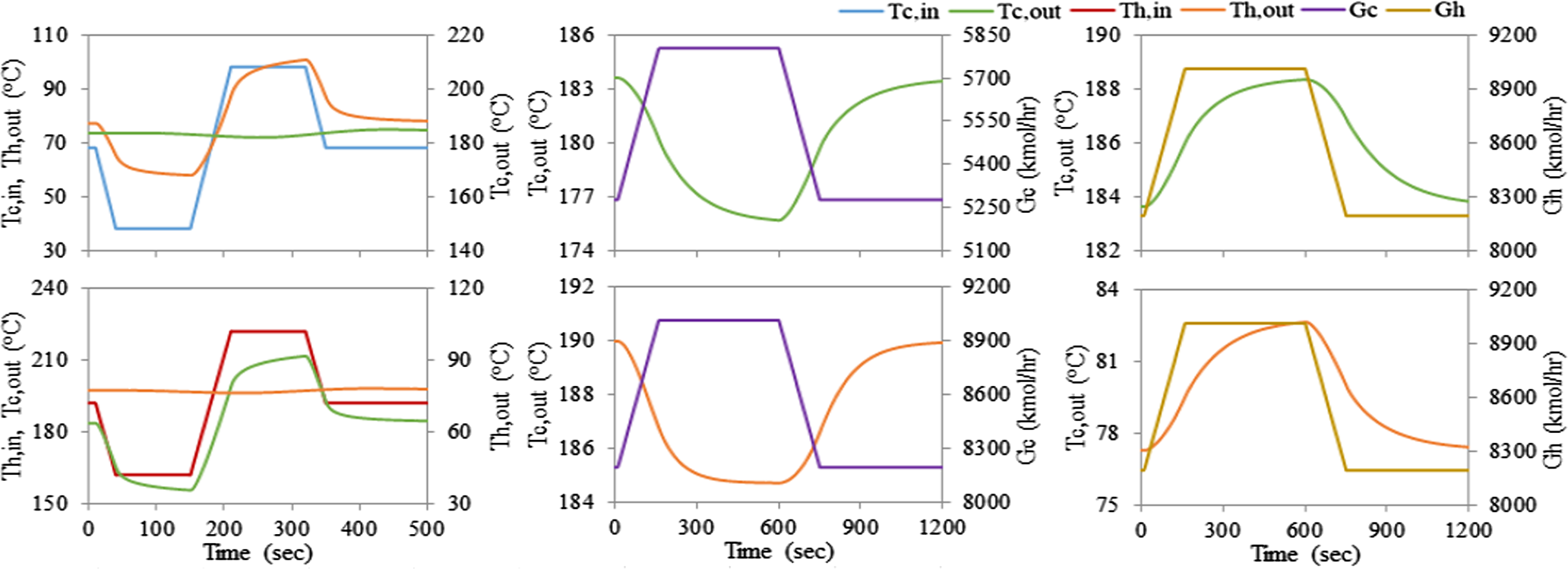
研究了在10兆瓦电sCO2再生式二氧化碳布雷顿循环电站中回热器的动态行为，通过引入不同速率的温度和流量斜坡进行分析。在快速斜坡率（30秒内入口温度升高30°C和150秒内流量增加10%）条件下，结果如图10和图12所示。在慢速斜坡率（60秒内入口温度升高30°C和150分钟内流量增加10%）条件下，结果如图11和图13。如图10–13所示，印刷电路热交换器对温度和流量变化的动态响应相对较快，这验证了针对超临界二氧化碳布雷顿循环最优设计的印刷电路热交换器由于其金属质量低且传热系数高而具有的预期性能。

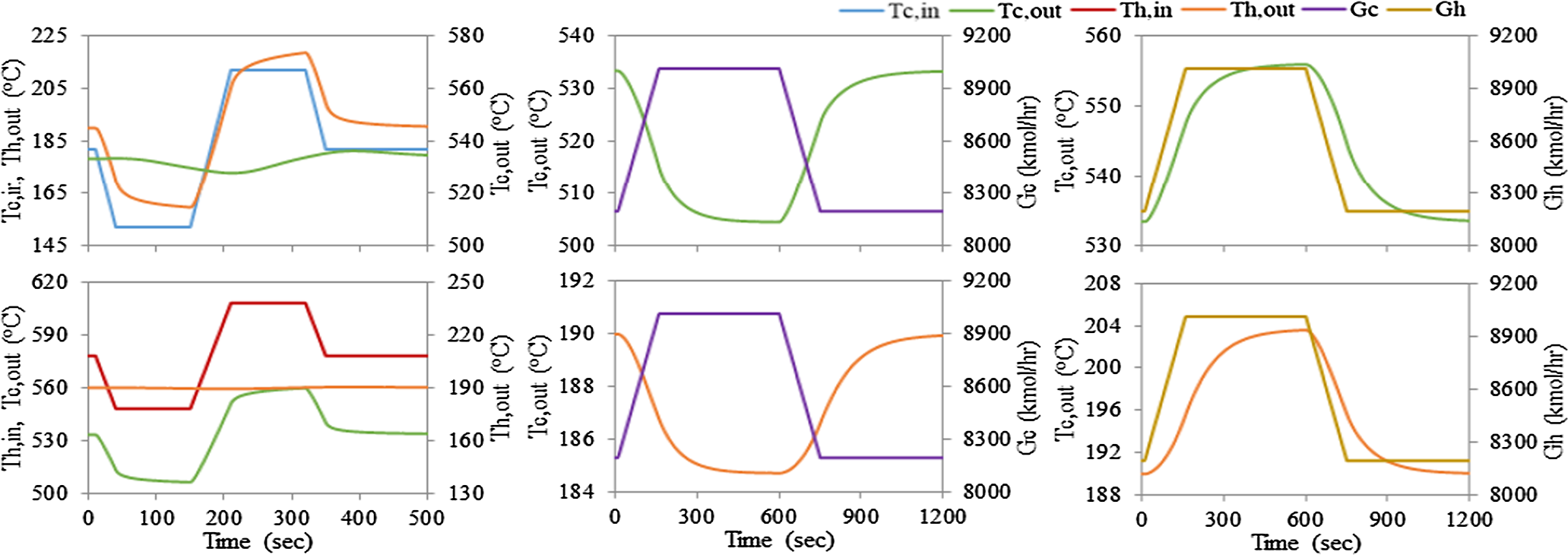
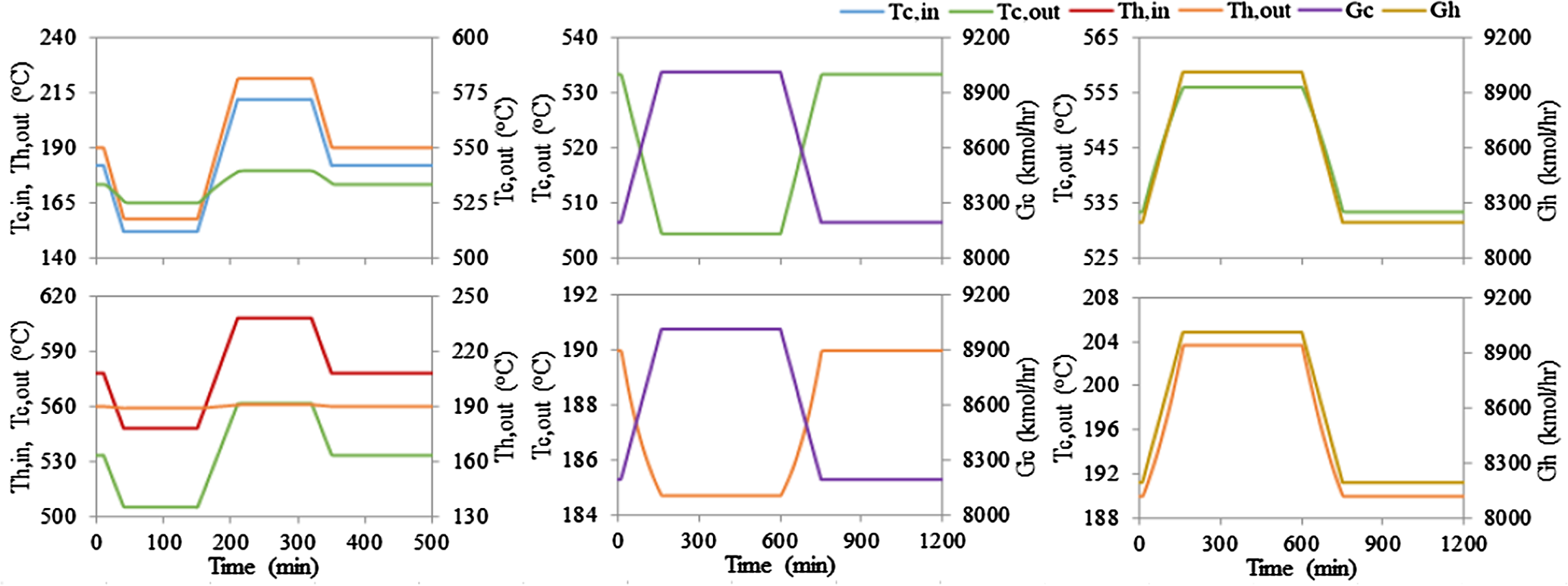
4.4. 不同换热器之间的比较

根据第4.2节给出的最优设计，对PCHEs在10兆瓦电sCO2再压缩闭式布雷顿循环电站中作为高温回热器和低温回热器的设计与动态行为进行了比较，比较对象为MSTEs和CSTEs，在相同的运行和设计工况下进行。本研究中，CSTEs使用Aspen Plus Dynamics中的HeatX模型进行模拟，其尺寸数据（AHX和MHX）通过Aspen换热器设计与评级(EDR)计算得到。仅考虑3/4英寸管（CSTEs中常用）和1/4英寸管（CSTEs中使用的最小管径），分别记为CSTEa和CSTEb。需要注意的是，在Aspen Plus Dynamics中模拟CSTEs时，Q是一个自由变量，由固定的UA值计算得出，这可能导致稳态传热速率存在轻微差异。MSTEs则基于作者先前报道的设计与动态模型，在ACM中进行设计和模拟[9,51,52]。各类回热器的关键设计措施汇总于表9中，而它们对冷侧入口温度阶跃升高30°C的动态响应如图14所示。注意，MHX包含了CSTEs和MSTEs的壳体质量。

表9中的结果表明，通过将管径从常规的3/4英寸（CSTEa）减小到最小的1/4英寸（CSTEb），CSTE的金属质量（MHX）可减少约50–60%。图14显示，时间常数也随之降低。为了进一步减少金属质量或提高动态响应速度，应考虑采用紧凑型换热器。根据Heatric的说法，设计合理的PCHE比常规CSTE体积和重量最多可减少85%[20]。如表9所示，由于MSTEs和PCHEs具有更小的通道直径（Do）或宽度（Dc），其传热系数（UHX）和紧凑性（A/V）显著提高，因此它们的金属质量（MHX）、流体滞留量（vHX）和传热面积（AHX）都小得多。根据当前的设计，若使用PCHE，回热器的尺寸可减少约72%，处于典型尺寸范围内。通过考虑其他流道设计和流动布置，可能进一步降低MHX[53]。MSTEs的紧凑度约为CSTEs的90%，并且由于MSTEs更高的紧凑度（A/V），甚至比PCHEs更轻[9]。另一方面，PCHEs通常结构更强，机械故障风险低于MSTEs。需要注意的是，MSTEs与PCHEs在低温回热器（LTR）上的关键设计措施差异大于高温回热器（HTR）。这是由于水力直径不同所致。对于HTR，MSTE的最优管径为2/32′′，与PCHEs中使用的通道宽度相似；而对于LTR，MSTE的最优管径为1/16′′，远小于PCHEs中使用的通道宽度（Heatric推荐为2毫米）[20]。因此，采用MSTE的LTR具有更高的紧凑度和换热效率。图14表明，MSTEs的动态响应略快于PCHEs，而两种紧凑型换热器的动态响应均远快于CSTEs，尤其是对于HTR。这是由于紧凑度和热质量的差异所致。

研究表明，PCHE仍然是CSTE的一种极具前景的替代方案，特别是对于sCO2动力循环中的回热应用，相较于MSTE，PCHE具有成熟的制造工艺、可靠的机械强度以及成功的实验室和工业经验。对于热侧和冷侧流量不平衡的低温回热器（LTR），由于其较小的压降、合理的金属质量以及丰富的制造和运行经验，1/4英寸CSTE仍然是10兆瓦电再压缩闭式布雷顿循环（RCBC）电厂的一个有前景的候选方案；尽管对于10兆瓦电电厂需要更多的集流管设计（3×2个壳体）将是一个缺点。

5. 结论

本研究使用在Aspen Custom Modeler中开发的一维模型，针对10兆瓦电超临界CO2再压缩闭式布雷顿循环装置中的高温回热器和低温回热器进行了印刷电路换热器的设计与仿真。两个模型均通过与用于100千瓦电设施的小型换热器实验数据对比进行了验证。优化设计结果表明，每块冷板对应两块热板并采用大角度通道的设计具有更少的金属质量，因此更适合大规模应用。采用印刷电路换热器的优化后高温回热器和低温回热器的重量分别为11.40吨和8.23吨。约为相同应用设计的传统管壳式换热器重量的70%。印刷电路换热器在入口温度变化时的时间常数小于15秒，在入口流量变化时约为1–2分钟，这比传统管壳式换热器短得多。用于超临界CO2布雷顿循环的不同类型换热器之间的比较表明，印刷电路换热器因其紧凑度、快速动态响应和成熟的制造工艺而成为一种有前景的候选方案。预计本研究开发的模型将被用于设计和制定在美国能源部STEP项目下于德克萨斯州圣安东尼奥建设的10兆瓦电示范电厂的控制和运行策略，该电厂已选用印刷电路换热器进行高温热回收。此外，这些模型还可作为涉及超临界流体和紧凑型换热器的放大应用及其他潜在应用的基准。