判断圆与射线是否相交

给定2个点的坐标A和B，代表有一条射线AB。
再给定一个点的坐标O点和一个半径R，代表以O为圆心以R为半径的一个圆。
问射线与圆是否有公共点，即存在某个点既在射线上又在圆上。
输入一共7个数，均为不超过100的非负整数。
输出一行，存在这个点就输出Y，否则输出N。
测试举例：
测试输入：2 3 2 100 2 1 1
预期输出：N
测试输入：1 0 1 100 2 1 1
预期输出：Y
向量乘法：
a∗b=∣a∣∗∣b∣∗cosxa * b = |a| * |b| * cosx
a∗b=∣a∣∗∣b∣∗cosx向量的坐标相乘：
(x1,y1)∗(x2,y2)=x1∗x2+y1∗y2(x1,y1)*(x2,y2)=x1 * x2+y1 * y2(x1,y1)∗(x2,y2)=x1∗x2+y1∗y2提示：

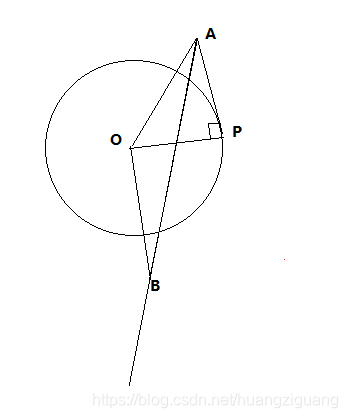
比较∠OAB和∠OAP的大小，如果∠OAB不大于∠OAP，则圆与射线相交。
可以通过比较sin值判断大小。

#include <iostream>
#include <cmath>
using namespace std;
int main()
{
   
   
 int x1,y1,x2,y2,xo,yo;
 double r,l,k=0;
 cin>>x1>>y1>>x2>>y2>>xo>>yo>>r;
 k=(y2-y1)/(x2-x1);
 l=abs(k