前言:
非递归实现归并排序,通常被称为 “自底向上”(Bottom-Up) 的归并排序,与递归版本(先将数组对半拆分直到只剩一个元素,再通过递归栈回溯合并)不同,非递归版本直接从最小的子数组(长度为1)开始,两两合并,然后长度翻倍(2, 4, 8 ...),直到合并完整个数组。

一、归并排序非递归的核心思路
递归算法转换为非递归实现主要有两种常见方法:
1.使用栈结构模拟递归过程
2.将递归逻辑改写为循环结构
1.1 栈模拟失效
如果仅通过栈结构模拟递归过程,我们只能够做到拆分数组,而不能做到合并数组。
假设我们要排序数组 arr = [8, 4, 5, 7],下标是 0 到 3。
初始状态:栈中有任务 [0, 3]。
第一步:弹出 [0, 3]。
①计算 mid = 1。
②拆分为左 [0, 1] 和右 [2, 3]。
③将 [2, 3] 和 [0, 1] 压入栈。
④关键点:[0, 3] 被彻底扔了,没人记得原本是要合并这俩段。
第二步:弹出 [0, 1]。
①计算 mid = 0。
②拆分为 [0, 0] 和 [1, 1]。
③将 [1, 1] 和 [0, 0] 压入栈。
④关键点:[0, 1] 也被扔了。
第三步:弹出 [0, 0]。
①区间长度为 1,是基本情况(Base Case),不需要做任何事。
②直接结束本次循环。
第四步:弹出 [1, 1],同上,直接结束。
问题出现了:此时 [0, 0] 和 [1, 1] 都处理完了。按理说,现在应该执行 merge(0, 0, 1) 把它们变成 [4, 8]。
但是!栈里没有这个指令,之前的 [0, 1] 早就被丢弃了,程序不知道这两个 1 长度的数组是“兄弟”关系。
后续:栈里剩下的 [2, 3] 也会经历同样的命运,被拆解成单元素后被遗忘。
1.2 循环结构实现
递归版本是“先拆分,后合并”,而非递归版本则是直接从最小的子数组开始“只合并”,不需要拆分。
核心原理如下:
①步长(gap)设为 1:首先将数组看作由 N 个长度为 1 的有序子数组组成。
②两两合并:相邻的两个长度为 1 的子数组合并成长度为 2 的有序子数组。
③步长翻倍:将步长设为 2,相邻的两个长度为 2 的子数组合并成长度为 4 的有序子数组。
④重复:步长继续翻倍(4, 8, 16...),直到步长超过数组长度,此时整个数组就有序了
简单理解:想象面前有一排乱序的扑克牌
①步长=1:先把相邻的 每1张 牌看作一组,两两合并成有序的 2张 牌。
②步长=2:再把相邻的 每2张 牌看作一组,两两合并成有序的 4张 牌。
③步长=4:继续合并为 8张……
④循环:直到步长超过数组长度,排序完成
二、归并排序非递归的实现流程
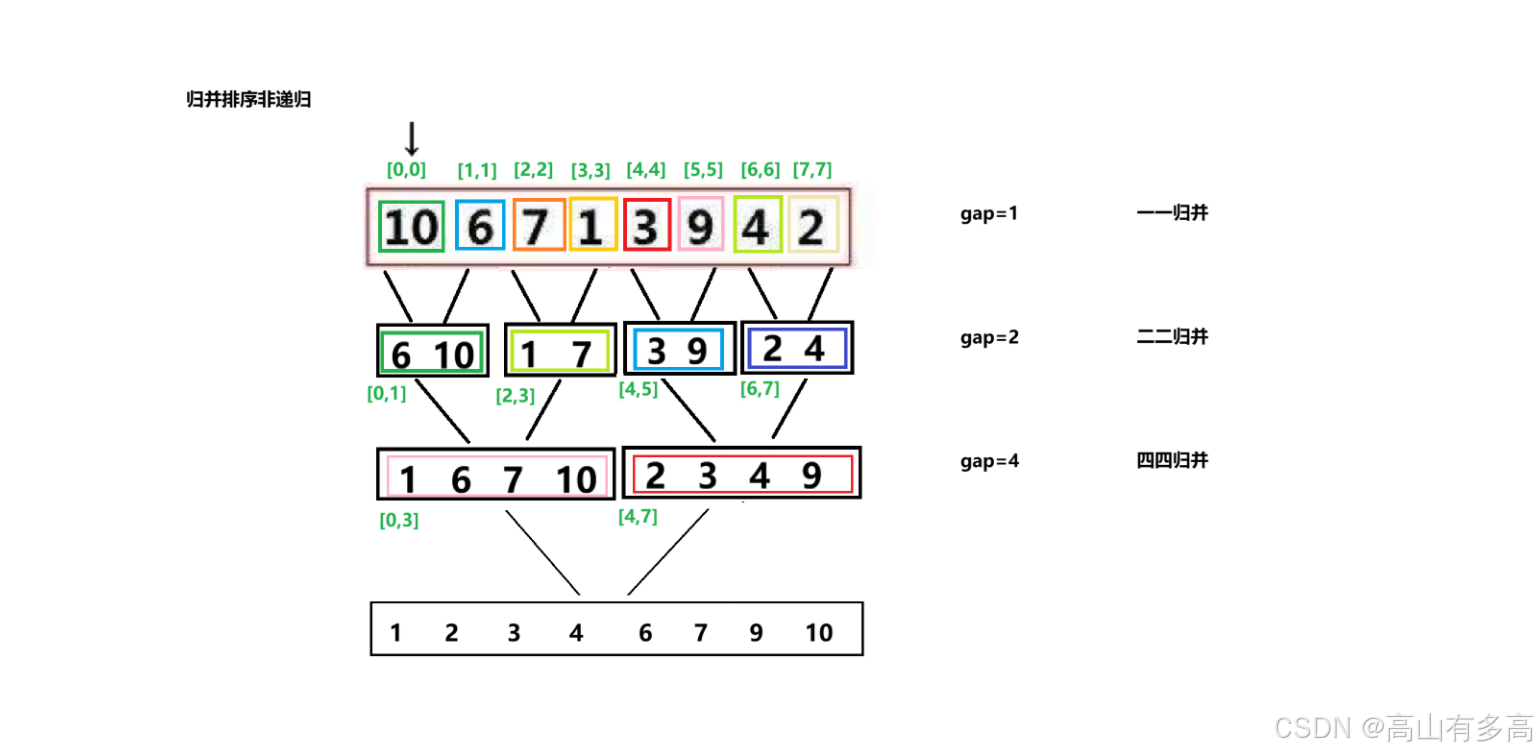
假设存在如下数组 [10, 6, 7, 1, 3, 9, 4, 2],一步一步演示循环结构是如何控制归并过程。
2.1核心变量回顾:
gap: 当前子序列的长度
左数组区间:[begin1 , end1]
begin1 :左半区间数组的起点 end1:左半区间数组的终点
右数组区间:[begin2,end2]
begin2:右半区数组的起点 end2 :右半区间数组的终点
2.2核心流程展示
第一轮:gap=1
1.第一次合并
左子数组:[0,0] => {10} 右子数组:[1,1] => {6}
begin1=0 end1=0 begin2=1 end2=1
即 [10] 和 [6] 操作: 6 小于 10,交换位置。
结果: [6, 10, 7, 1, 3, 9, 4, 2]
2.第二次合并
左子数组:[2,2] => {7} 右子数组: [3,3] => {1}
begin1=2 end1=2 begin2=3 end2=3
即 [7] 和 [1] 操作: 1 小于 7,交换位置。
结果: [6, 10, 1, 7, 3, 9, 4, 2]
3.第三次合并
左子数组:[4,4] => {3} 右子数组: [5,5] => {9}
begin1=4 end1=4 begin2=5 end2=5
即 [3] 和 [9] 操作: 3 小于 9,无需变动(本来就有序)。
结果: [6, 10, 1, 7, 3, 9, 4, 2]
4.第四次合并
左子数组:[6,6] => {4} 右子数组: [7,7] => {2}
begin1=6 end1=6 begin2=7 end2=7
即 [4] 和 [2] 操作: 2 小于 4,交换位置。
第一轮结束,此时数组变成了两两有序:[6, 10, 1, 7, 3, 9, 2, 4]
第二轮:gap=2
1.第一次归并
左子数组:[0,1] => {6,10} 右子数组: [2,3] => {1,7}
begin1=0 end1=1 begin2=2 end2=3
归并过程:
比较 6 和 1 -> 取 1
比较 6 和 7 -> 取 6
比较 10 和 7 -> 取 7
剩下 10 -> 取 10
结果: [1, 6, 7, 10, 3, 9, 2, 4]
2.第二次归并
左子数组:[4,5] => {3,9} 右子数组:[6,7] => {2,4}
归并过程:
比较 3 和 2 -> 取 2
比较 3 和 4 -> 取 3
比较 9 和 4 -> 取 4
剩下 9 -> 取 9
结果: [1, 6, 7, 10, 2, 3, 4, 9]
第二轮结束,此时数组变成了四四有序:[1, 6, 7, 10, 2, 3, 4, 9]
第三轮:gap= 4
1.第一次归并
左子数组:[0,3] => {1, 6, 7, 10} 右子数组:[4,7] => {2, 3, 4, 9}
begin1=0 end1=3 begin2=4 end2=7
归并过程:
1 vs 2 -> 取 1
6 vs 2 -> 取 2
6 vs 3 -> 取 3
6 vs 4 -> 取 4
6 vs 9 -> 取 6
7 vs 9 -> 取 7
10 vs 9 -> 取 9
剩下 10 -> 取 10
结果: [1, 2, 3, 4, 6, 7, 9, 10]
第三轮结束,数组完全有序 [1, 2, 3, 4, 6, 7, 9, 10]
三、归并排序非递归的疑难点
3.1满足左右数组均分
归并排序的逻辑结构是基于“完全二叉树”,当满足每一步都能凑齐完美的“左半边”和“右半边”
步长 1:8=1+1+1+1+1+1+1+1(完美)
步长 2:8=2+2+2+2(完美)
步长 4:8=4+4(完美)
步长 8:8=8(完美)
如下图示:假设存在一个数组 [10 6 7 1 3 9 4 2]

3.2不满足左右数组均分
这个问题的根本原因在于:归并排序的逻辑结构是基于“完全二叉树”的(总是 1→2→4→8),而现实中的数组长度 往往不是 2 的整数次幂,因为 2^k的倍增网格无法完美覆盖任意整数 N,多出来的部分就是所谓的“边界问题”。
步长 1:10= 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1(完美,因为 10 是偶数)
步长 2:10 = 2 + 2 + 2 + 2 + 2 (最后一个数组落单)
步长 4:10 = 4 + 4 + 2 (最后一个数组落单)
步长 8:10 = 8 + 2 (最后一个数组落单)
如下图示:假设存在一个数组[6 1 2 7 9 3 4 5 10 8]
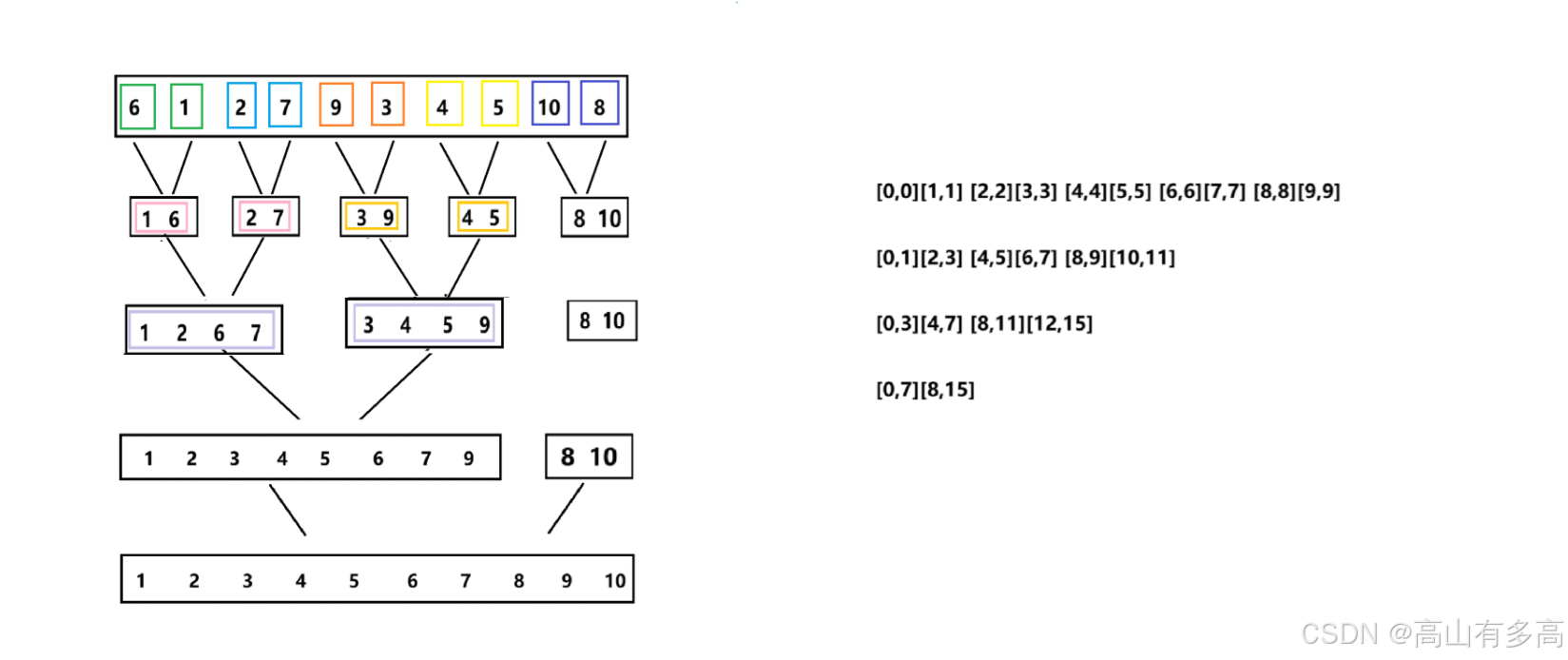
3.2.1 不均分引起的问题
我们注意到:如下四个边界中,只有左半区间数组的起点能够满足严格在数组下标的索引中,其余边界均有可能有越界的风险,所以我们要控制边界问题
begin1 :左半区间数组的起点 end1:左半区间数组的终点
begin2:右半区数组的起点 end2 :右半区间数组的终点

3.2.2 解决方案
我们可以将该问题其分为两组进行讨论:
问题1. (情况二、情况三)当begin2出现越界时(begin2 >= n),即当前左子数组出现落单,如下图所示的左数组元素为:{8,10}
问题2. (情况一)当仅有end2出现越界时 (end2 >= n) ,即当前出现的是长度不对等进行归并,如下图所示:{1,2,3,4,5,6,7,9} 与 {8,10}
解决1:若当begin2出现越界时,即出现数组落单,不需要对其进行归并排序,我们可以直接跳过
解决2:当仅有end2出现越界时,即当前左数组和右数组进行的是不对等长度归并,我们需要进行修正右数组,将end2修正为 n-1 即可。

3.3递归与非递归的区别
你可能会疑惑:“为什么递归版本的归并排序,好像没有这么多复杂的边界判断?
答案的核心的是:递归(自顶向下)拥有 “自动适应” 的灵活性,而非递归(自底向上)则带有 “按规则执行” 的僵硬性—— 两者的核心逻辑差异,直接导致了边界处理的复杂度不同。
3.3.1递归:顺势而为,自然适配
核心思路:不预设任何拆分规则,只遵循 “把当前数组切两半” 的核心逻辑,直到子数组长度为 1(不可再拆)。
关键特点:自动停止,无需刻意判断边界
递归的拆分完全依赖 “当前区间的实际长度”:
比如数组长度
N=6,会先切成[0,2]和[3,5](各 3 个元素);左区间
[0,2]再切成[0,0]和[1,2](1 个 + 2 个元素);右区间
[3,5]同理切成[3,4]和[5,5];直到子数组长度为 1(如
[0,0]),递归自然终止(因为left >= right,不再继续拆分)。
它不关心 “整体数组长度是多少”,只聚焦 “当前手里的区间有几个元素”,拆分过程顺势而为,边界会自然收敛,无需额外处理 “框选超出范围” 的问题。
3.3.2非递归:刻舟求剑,需手动补漏
核心思路:不进行 “拆分”,而是从最小步长(长度 1)开始,按固定规则 “合并”,严格遵循 1→2→4→8→… 的翻倍逻辑,用固定尺寸的 “框” 去框选相邻子数组进行合并。
关键特点:规则固定,必须处理边界溢出
非递归的合并规则是 “僵硬” 的,固定尺寸的 “框”(gap)不会因数组长度调整:
比如数组长度
N=6,当 gap=4时,按规则会尝试框选[0,3]和[4,7]两个区间合并;但数组实际长度只有 6,
[4,7]会超出数组边界(最大索引为 5),此时必须手动判断并修正右边界(比如将 end2 设为N-1=5)。
这种 “按固定规则框选” 的逻辑,就像 “刻舟求剑”—— 不管数组实际长度是否匹配,先按规则执行,再处理因 “框太大” 导致的边界溢出问题,这也是非递归版本需要额外边界判断的核心原因。
四、代码实现
void MergeSortNonR(int* a, int n)
{
//申请一个临时数组
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail\n");
return;
}
//自底向上进行归并,初始时进行 “1 1” 归并
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
//begin1 :左半区间数组的起点 end1:左半区间数组的终点
int begin1 = i, end1 = i + gap - 1;
//begin2:右半区数组的起点 end2:右半区间数组的终点
int begin2 = i + gap, end2 = i + gap * 2 - 1;
//出现数组落单不需要进行归并
if (begin2 >= n) break;
//出现不对等长度匹配,修正end2
if (end2 >= n) end2 = n - 1;
//归并到tmp数组的起始位置
int j = begin1;
//进行一组归并
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[j++] = a[begin1];
begin1++;
}
else
{
tmp[j++] = a[begin2];
begin2++;
}
}
//处理未归并完的左子数组
while (begin1 <= end1)
{
tmp[j++] = a[begin1];
begin1++;
}
//处理未归并的右子数组
while (begin2 <= end2)
{
tmp[j++] = a[begin2];
begin2++;
}
//归并一组拷贝一组
memcpy(a+i, tmp+i, sizeof(int) * (end2 - i + 1));
}
//gap变化为:1—>2->4->8->16...
//“1 1” 归并 “2 2” 归并 “4 4” 归并 ...
gap *= 2;
printf("\n");
}
free(tmp);
}
既然看到这里了,不妨关注+点赞+收藏,感谢大家,若有问题请指正。


 归并排序非递归详解
归并排序非递归详解























 1023
1023










