前言:
选择排序(Selection Sort)是一种基础的排序算法,其核心思路是:在每一轮遍历中,从剩余未排序元素中选出最小(或最大)值,并将其放置在已排序序列的末端。
对于排序算法的实现,由局部到整体的思路,先排序好一趟或一个元素,再排列多趟或全部元素。

一、选择排序的工作原理
以排序升序数组为例,工作原理如下:
初始化:假设当前数组中,前部分是已经排好序的,后部分是未排序的。
寻找最小(或最大)值:遍历未排序的部分,找出其中的最小值(或最大值)。
交换位置:将找到的最小值与当前未排序部分的第一个元素交换。
重复:缩小未排序部分的范围,重复以上步骤,直到整个数组排好序。
如下动图所示:
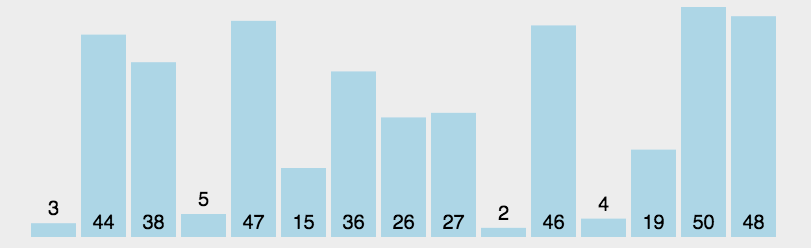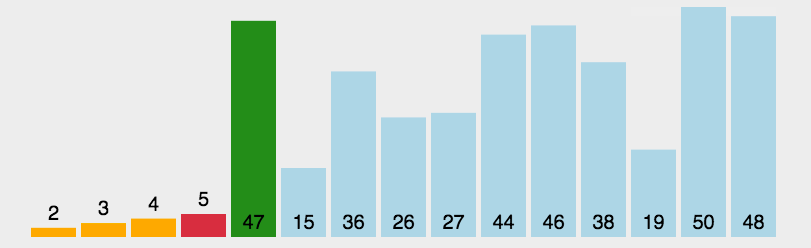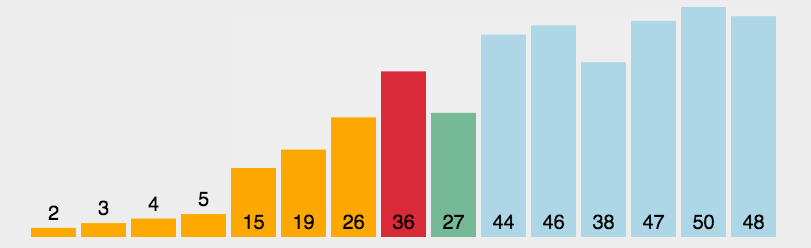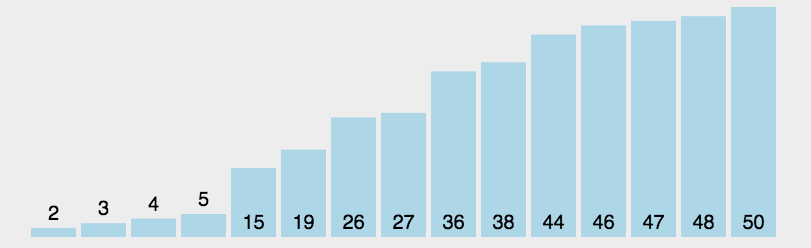
以上述数组为例,假设有一个待排列的数组为:[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48]。
第一轮排序:
当前未排序部分:[3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]
最小的值是 2。
将 2 和未排序部分的第一个元素 3 交换,数组变为:[2, 44, 38, 5, 47, 15, 36, 26, 27, 3, 46, 4, 19, 50, 48]
第二轮排序:
当前未排序部分:[44, 38, 5, 47, 15, 36, 26, 27, 3, 46, 4, 19, 50, 48]
最小值是 3。
将 3 和未排序部分的第一个元素 44 交换,数组变为:[2, 3, 38, 5, 47, 15, 36, 26, 27, 44, 46, 4, 19, 50, 48]
第三轮排序:
当前未排序部分:[38, 5, 47, 15, 36, 26, 27, 44, 46, 4, 19, 50, 48]
最小值是 4。
将 4 和未排序部分的第一个元素 38 交换,数组变为:[2, 3, 4, 5, 47, 15, 36, 26, 27, 44, 46, 38, 19, 50, 48]
第四轮排序:当前未排序部分:[5, 47, 15, 36, 26, 27, 44, 46, 38, 19, 50, 48]
最小值是 5(它已经排好序,所以不需要交换)。
数组仍然是:[2, 3, 4, 5, 47, 15, 36, 26, 27, 44, 46, 38, 19, 50, 48]
第五轮排序:
当前未排序部分:[47, 15, 36, 26, 27, 44, 46, 38, 19, 50, 48]
最小值是 15。
将 15 和未排序部分的第一个元素 47 交换,数组变为:[2, 3, 4, 5, 15, 47, 36, 26, 27, 44, 46, 38, 19, 50, 48]
第六轮排序:
当前未排序部分:[47, 36, 26, 27, 44, 46, 38, 19, 50, 48]
最小值是 19。
将 19 和第一个元素 47 交换,数组变为:[2, 3, 4, 5, 15, 19, 36, 26, 27, 44, 46, 38, 47, 50, 48]
第七轮排序:
当前未排序部分:[36, 26, 27, 44, 46, 38, 47, 50, 48]
最小值是 26。
将 26 和第一个元素 36 交换,数组变为:[2, 3, 4, 5, 15, 19, 26, 36, 27, 44, 46, 38, 47, 50, 48]
第八轮排序:当前未排序部分:[36, 27, 44, 46, 38, 47, 50, 48]
最小值是 27。
将 27 和第一个元素 36 交换,数组变为:[2, 3, 4, 5, 15, 19, 26, 27, 36, 44, 46, 38, 47, 50, 48]
第九轮排序:
当前未排序部分:[36, 44, 46, 38, 47, 50, 48]
最小值是 36(它已经排好序,所以不需要交换)。
数组仍然是:[2, 3, 4, 5, 15, 19, 26, 27, 36, 44, 46, 38, 47, 50, 48]
第十轮排序:
当前未排序部分:[44, 46, 38, 47, 50, 48]
最小值是 38。
将 38 和第一个元素 44 交换,数组变为:[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 46, 44, 47, 50, 48]
第十一轮排序:
当前未排序部分:[46, 44, 47, 50, 48]
最小值是 44。
将 44 和第一个元素 46 交换,数组变为:[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 50, 48]
第十二轮排序:
当前未排序部分:[46, 47, 50, 48]
最小值是 46(它已经排好序,所以不需要交换)。
数组仍然是:[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 50, 48]
第十三轮排序:
当前未排序部分:[47, 50, 48]
最小值是 47(它已经排好序,所以不需要交换)。
数组仍然是:[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 50, 48]
第十四轮排序:
当前未排序部分:[50, 48]
最小值是 48。
将 48 和第一个元素 50 交换,数组变为:[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
第十五轮排序:当前未排序部分:[50]
只有一个元素,已经排好序,排序完成。
最终排序结果:[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
二、选择排序的代码实现
void SelectSort(int* a, int n)
{
//i控制的逻辑:需要n-1趟排序才能使得待排数组有序
for (int i = 0; i < n; i++)
{
//默认最小值下标为未排序元素中的第一个
int min_index = i;
//j控制的逻辑:一趟排序中,寻找未排序元素的最小值所在的位置
//不与自己比较,从i+1开始寻找
for (int j = i+1; j < n ; j++)
{
if (a[j] < a[min_index])
{
//更新下标
min_index = j;
}
}
//交换
Swap(&a[i], &a[min_index]);
}
}
三、选择排序的优化
当前版本的选择排序算法在每轮遍历中仅能确定一个最小值(或最大值)。我们考虑对其进行优化,使每轮排序能同时确定最大值和最小值,将最小值置于数组前端,最大值置于末尾,通过这种双端选择的方式,可显著提升排序效率。
void SelectSort(int* a, int n)
{
//定义两个位置,
//begin:存放一趟排序中选出的最小值
int begin = 0;
//end:存放一趟排序中选出的最大值
int end = n - 1;
while (begin < end) //当begin>=end时,待排数组已经有序
{
//定义两个下标
//mini:指向未排序元素中的最小值的下标
//maxi:指向未排序元素中的最大值的下标
//两者默认都初始化为begin
int mini=begin;
int maxi=begin;
//i控制的逻辑:遍历未排序的数组元素
for (int i = begin+1; i <= end; i++)
{
if (a[i] < a[mini]) mini = i;
if (a[i] > a[maxi]) maxi= i;
}
//找到了最小值元素的下标,进行交换
Swap(&a[begin], &a[mini]);
//特别注意,若maxi在begin位置上
//将a[begin]与a[mini]交换后,此时最大值的元素被换在了mini的位置
//所以此时maxi的下标要更新未mini
if (maxi == begin)
{
maxi = mini;
}
//找到了最大值元素的下标,进行交换
Swap(&a[end], &a[maxi]);
begin++;
end--;
}
}
一般情况:
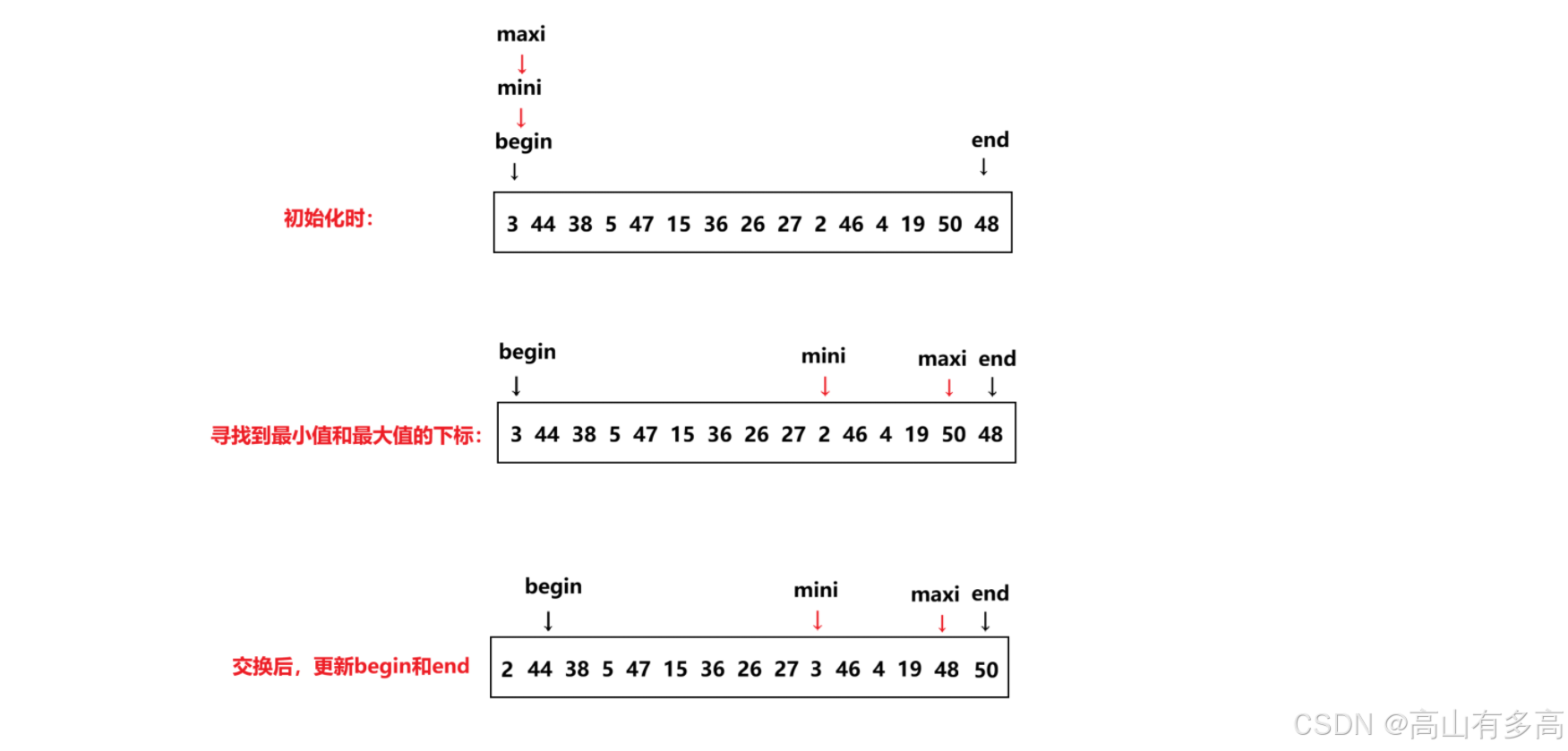
特殊情况:

四、选择排序的时空复杂度
4.1 时间复杂度
无论最好、最坏还是平均情况,选择排序的时间复杂度都是:O(n^2)
简单推导如下:
第 1 趟:从 n 个元素里找最小值,要比较 n−1次
第 2 趟:从剩下的 n-1 个元素里找最小值,要比较 n−2次
…
第 n-1 趟:比较 1 次
比较总次数为:(n−1) + (n−2) + ⋯ + 2 + 1 = ( n - 1 ) * n / 2
故而时间复杂度为O(n^2)
4.2 空间复杂度
选择排序是原地排序,只需要常数个辅助变量(如保存当前最小值下标等),不需要额外开辟与 n 成比例的空间。
因此空间复杂度为:O(1)
既然看到这里了,不妨关注+点赞+收藏,感谢大家,若有问题请指正。


 选择排序算法详解
选择排序算法详解





















 786
786










