排序算法指南：归并排序

前言：

        归并排序的核心思想是利用分治法（Divide and Conquer）策略，它将一个大的问题分解成小的、容易解决的子问题，然后将子问题的解合并起来，从而得到原问题的解。

                                                        

        

一、归并排序的核心思想

        

分（Divide）: 将待排序的数组（或列表）不断地分成两个子数组，直到每个子数组只包含一个元素（单个元素被认为是天然有序的）。

        

治（Conquer）: 对每个只含一个元素的子数组进行排序（实际上它们已经是有序的）

        

合（Merge）: 将两个已排序的子数组归并成一个更大的有序数组，重复这个过程，直到所有子数组都归并成一个完整的有序数组。

        

        

二、归并排序的工作流程

        

2.1分区间

        

分： 从宏观上看，把数组切成了两半，但在计算机程序的微观实现中，我们并没有真正拿刀去把数组“切断”，

        而是通过数组下标（Index）来计算和控制范围,  “一分为二” 的核心在于计算中间位置（Mid）。

        

核心公式:   假设我们要处理的数组范围是从下标 left 到 right （从左到右）

                

mid= (left + right) / 2

                

所以，我们要将数组从逻辑上分为两个部分：

                

①左半部分范围： [left, mid]

                

②右半部分范围： [mid + 1, right]        

        

有读者肯定疑惑:

        

为什么左半部分范围是：[left , mid] ，右半部分范围是: [mid+1 , right]

        

而不能是左半部分范围为：[left, mid-1]   右半部分范围为: [mid , right]  

        

 答：这是因为：mid=(left + right) / 2  为整数除法，在大多数编程语言中，会自动向下取整，比如 3.5 会变成 3，

        所以 mid 必须归属于左半部分，这样才能保证左右两边在每一次递归中范围都在真正缩小。       

        

        

举例说明：假设有如下数组为： [3 , 4]   下标索引为：[ 0 , 1]

        

计算mid ： (0 + 1) / 2 =0

        

错误划分:   

                      

若按照左半部分：[left , mid-1]  右半部分：[mid , right]   

        

左半部分为：[0 , -1]  (范围无效，程序崩溃)

        

右半部分为: [ 0 ,1]  （死循环！ 范围根本没有变小，还是原来的 0 到 1，递归永远停不下来）   

        

        

正确划分：

        

按照左半部分：[left , mid]  右半部分：[mid+1 , right]

        

左半部分为：[0 , 0]  (只有一个元素，停止递归)

        

右半部分为：[1, 1]   (只有一个元素，停止递归)   

        

示例：假设存在数组：[10, 6, 7, 1, 3, 9, 4, 2]

        

        

        

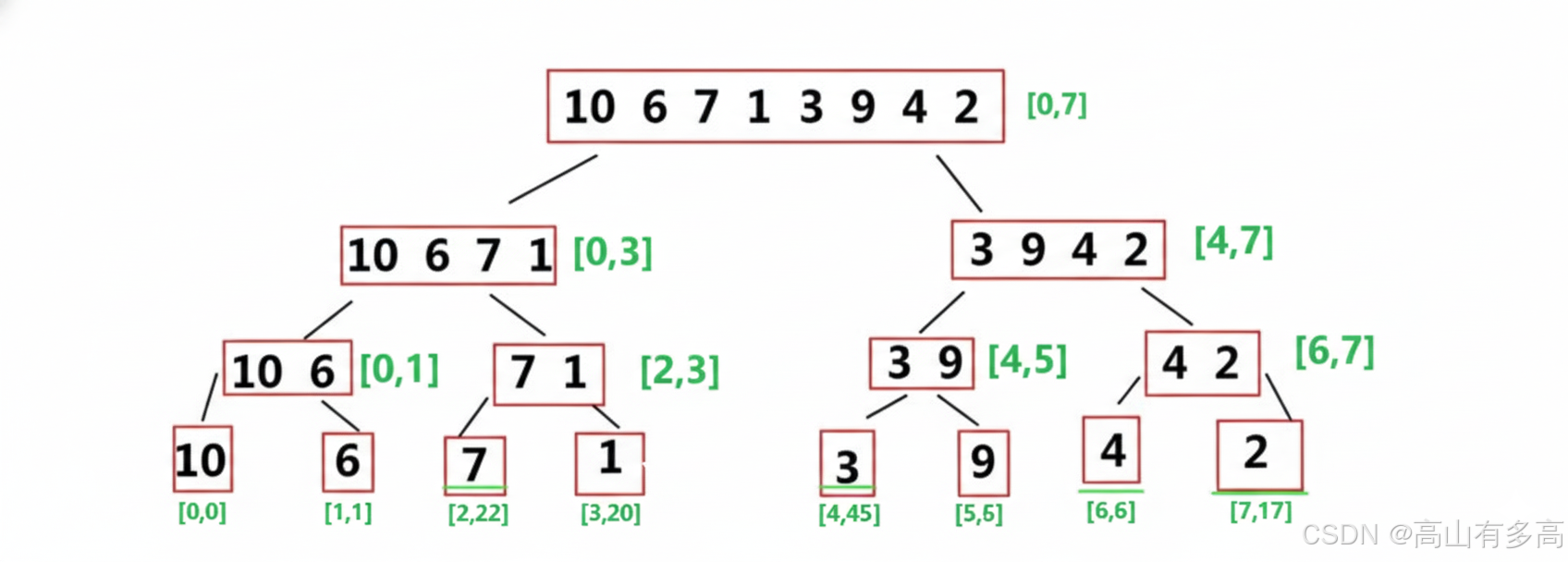
2.2治区间

        

治：对每个只含一个元素的子数组进行排序（实际上它们已经是有序的）

       

示例：只有一个区间的元素逻辑上认为有序：[10]     [6]    [7]    [1]    [3]    [9]    [4]    [2]

        

        

2.3合区间

        

合（Merge）: 将两个已排序的子数组归并成一个更大的有序数组，重复这个过程，直到所有子数组都归并成一个完整的有序数组

        

示例：将上述最小区间进行合并，知道所有子数组都归并成一个完完整区间

        

        

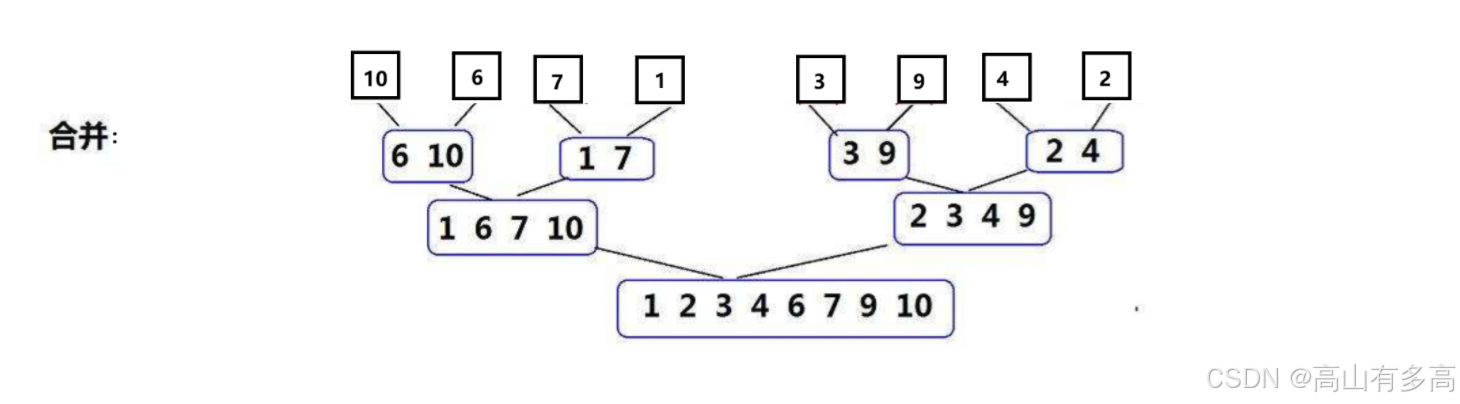
三、代码实现

        

//left：  区间的起始下标
//right： 区间的终止下标
void _MergeSort(int *a,int * tmp,int left,int right)
{
    //当子区间只有一个元素，则不需要进行切分
	if (left == right) return;

    //计算中间下标
	int mid = left + (right - left) / 2;

	//左区间范围：[left,mid] 
	_MergeSort(a, tmp, left, mid);
    
    //右区间范围：[mid+1,right]
	_MergeSort(a, tmp, mid + 1, right);

	//合并左区间和右区间
    //begin1：左区间起始位置，end1：左区间终止位置
	int begin1 = left, end1 = mid;
    
    //begin2：右区间起始位置，end2：右区间终止位置
	int begin2 = mid + 1, end2 = right;
    
    //存放在tmp数组中的起始位置
	int i = left;
    
    //进行合并数组
	while (begin1<=end1 && begin2<=end2)
	{
		if (a[begin1]<a[begin2])
		{
			tmp[i++] = a[begin1];
			begin1++;
		}
		else
		{
			tmp[i++] = a[begin2];
			begin2++;
		}

	}
	//左数组  [begin1,end1] 有剩余元素
	while (begin1 <= end1)
	{
		tmp[i++] = a[begin1];
		begin1++;
	}

	//右数组  [begin2,end2] 有剩余元素,
	while (begin2 <= end2)
	{
		tmp[i++] = a[begin2];
		begin2++;
	}

	//将tmp数组的元素拷贝回a数组中
	memcpy(a+left, tmp+left , sizeof(int) * (right - left  + 1));
	

}


//数组a：待排序数组
//    n：数组中元素个数
void MergeSort(int* a, int n)
{
    //通过创建临时数组
	int * tmp =(int* )malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail\n");
		return;
	}
    
    //进行归并排序
	_MergeSort(a, tmp, 0, n - 1);
    
    //释放临时数组
	free(tmp);
}

      

3.1疑难点分析      

        

疑难点： 为什么不是 int i = 0？ 既然我们在合并一个新的小段，为什么不从 tmp 的第 0 个位置开始存呢？

        

答：简单来说，我们在临时数组 tmp 中用于存放排序结果的起始位置，必须与当前正在处理的原始数组 a 的起始位置 left 保持一致。

       核心原因：tmp 是全局共用的大数组，在归并排序的经典实现中，tmp 数组通常是在最外层一次性开辟的，大小和原数组一致。

       它不是每次递归都新建的小数组，而是全局共用的大数组。

             

场景模拟：假设数组是 [10, 6, 7, 1, 3, 9, 4, 2]，长度为 8。

        

1.第一次合并左半部分（处理下标 0 到 3 的元素 [10, 6, 7, 1]）时：

        

①left = 0

        

②int i = left;

         

③此时i=0，将数据写入 tmp[0] 到 tmp[3]，这是正确的。

        

2.第二次合并右半部分（处理下标 4 到 7 的元素 [3, 9, 4, 2]）时：

        

①left = 4

        

②right = 7

        

③如果我们错误地设置 int i = 0：

        

我们会把右半边排序好的数据写到  tmp[0],  tmp[1],  tmp[2],  tmp[3]，这会覆盖掉左半边刚刚排好序、存放在 tmp[0...3] 的数据！

        

如果我们设置 int i = left，此时 i = 4 ：

        

我们会把数据写到 tmp[4], tmp[5], tmp[6], tmp[7]。这避免了数据覆盖，并且正是它们在原数组中应该待的位置。

        

        

3. 为最后的 memcpy 铺路 (代码的简洁性)

        

请看函数最后那句拷贝代码：

        

memcpy(a + left, tmp + left, sizeof(int) * (right - left + 1));

• a + left: 指向原数组中当前段的起始位置。

• tmp + left: 指向临时数组中当前段的起始位置。

        

正是因为最开始写了 int i = left;

        

这样数据被乖乖地写在了 tmp 数组的 [left ... right] 范围内。

        

所以在最后拷贝回去的时候，我们才能直接用 tmp + left 找到这段数据，和 a + left 完美对应，让拷贝操作简洁而高效。

        

        

4. 总结

        

• left: 告诉我们当前任务是从原数组的哪里开始的。

        

• i = left: 确保我们在临时数组里操作时，位置（下标）和原数组保持一致。

        

这样设计的好处是逻辑非常清晰：tmp[k] 永远对应 a[k] 的原始内存地址，不会出现错位。

        

四.归并排序的复杂度

4.1时间复杂度

        

纵向（树高）：每次对半切分，直到子数组大小为 1，则其复杂度为：log₂n。

        

以待排数组有n个元素为例：     

层级 (Level)                     数据规模 (Size)                      节点数量 (Nodes)
-------------------------------------------------------------------------------------

第 0 层:                        [     n     ]                             1 个
(初始状态)                      /           \

第 1 层:                  [ n/2 ]           [ n/2 ]                       2 个
(切分1次)                /      \           /      \

第 2 层:             [ n/4 ]   [ n/4 ]   [ n/4 ]   [ n/4 ]                4 个
(切分2次)             /   \     /   \     /   \     /   \

  ...                   ...       ...       ...       ...                 ...

第 m 层:           [1] [1] [1] [1] ... ... [1] [1] [1] [1]                n 个
(终止状态)         
                

        

横向（每层工作量）：每一层都需要将所有元素进行一次合并操作，需要遍历一遍整个数组，则其复杂度为：O(n)。

        

以待排元素有n个为例

第 1 层：合并两个n/2的数组，遍历 n 次。

第 2 层：合并四个n/4的数组，遍历 n 次

...
    
第 n 层: 合并一个n的数组，总共还是遍历n次
    
每一层的工作量 = O(n)

        

故而总的时间复杂度为：O(n * logn)

        

4.2空间复杂度

        

1. 辅助数组空间（主导因素）：需开辟临时辅助数组（通常命名为 tmp ），用于暂存合并后的有序元素，避免直接修改原数组导致数据混乱。

                                                 必须开辟与原数组大小相等的临时空间，空间复杂度为 O（n），这是归并排序空间开销的核心来源

                                                                

2. 递归栈空间：归并排序基于分治法，通过递归调用将数组不断拆分为子数组，递归过程中需使用栈存储函数调用栈帧

                          递归树高度为log₂n ，所以需要O(log n)的空间，远小于辅助数组的 O（n），通常可忽略其对整体空间复杂度的影响。

        

故而空间复杂度为O(n)

既然看到这里了，不妨关注+点赞+收藏，感谢大家，若有问题请指正。