排序算法指南：快速排序(非递归)

原创已于 2025-12-07 15:57:46 修改 · 703 阅读

43 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构 #c语言 #开发语言 #算法 #c++ #排序 #快速排序

于 2025-12-07 15:41:49 首次发布

数据结构与算法专栏收录该内容

20 篇文章

订阅专栏

编程达人挑战赛·第5期 10w+人浏览 279人参与

前言：

本文将通过图解与代码相结合的方式，详细介绍快速排序的非递归实现方法。虽然前文已展示递归实现方案，但在实际面试中，面试官更倾向于考察非递归版本的实现。这种实现方式不仅能加深对算法的理解，还能展现应聘者对栈结构的掌握程度。

一、非递归实现快排的思路

1.1核心原理：手动模拟栈

在标准的递归快速排序中，当我们写下 quickSort(a,left, right) 时，系统会自动分配一块内存（函数调用栈）来记住当前的 left 和 right 是多少，以及函数执行完后该回到哪里。

在非递归版本中，我们不需要系统帮忙，而是自己创建一个栈（Stack）数据结构。

1.2核心操作：用栈存取数组区间

① 向栈中存储操作：存储每一次需要排序的子数组的起止下标（begin，end）。

由于栈的特性是先进后出，我们优先处理左区间，再处理右区间，类似于二叉树的前序操作。

故而在存储的时候优先存储右区间，再进行存储左区间。

② 向栈中拿取操作： 每次从栈里拿出一对下标，对这段范围进行“分区操作”，然后把产生的新范围（左半区和右半区）再扔回栈里。

二、用栈来模拟存储区间

假设存在数组a为: [6, 1, 2, 3, 4, 5, 9, 7, 10, 8]

下标: [0 1 2 3 4 5 6 7 8 9]

定义int left1 ：左区间数组的起始位置下标

定义int right1 ：左区间数组的终止位值下标

则左区间数组的范围是：[left1 , right1]

定义int left2 ：右区间数组的起始位置下标

定义int right2 ：右区间数组的终止位置下标

则右区间数组的范围是：[left2，right2]

第一步：初始化栈



准备一个空栈，先把整个数组的任务扔进去：入栈：[0, N-1]





第二步：循环处理





这是一个while(栈非空)的循环：



1.弹栈（Pop）：拿出一个任务（begin，end）。



2.分区（Partition）：通过Hoare分区法进行分割当前处理任务，keyi = PartitionSlowFast(a, begin, end);



  将其分为 [begin , keyi - 1] keyi [keyi+1 , end]



3.记录左右区间：记录左区间 left1 = begin right1=keyi-1 即： [left1 , right1]



记录右区间 left2 = keyi+1 right2=end 即：[left2, right2]



4.入栈左右区间：优先压入右区间，再压入左区间，因为栈是“后进先出”，这样下一轮循环就会先处理左边，模拟递归的顺序。



压入右区间：push (right2) -> push(left2)



  压入左区间： push (right1) -> push(right2)



  (💡 小贴士：区间只有一个元素不入栈，区间不存在也不入栈 )





第三步：栈为空



        当栈变空时，说明所有的大区间都被切成了小区间，小区间都被切没了（排序完成），数组就有序了！🎉

区间分割如图所示：

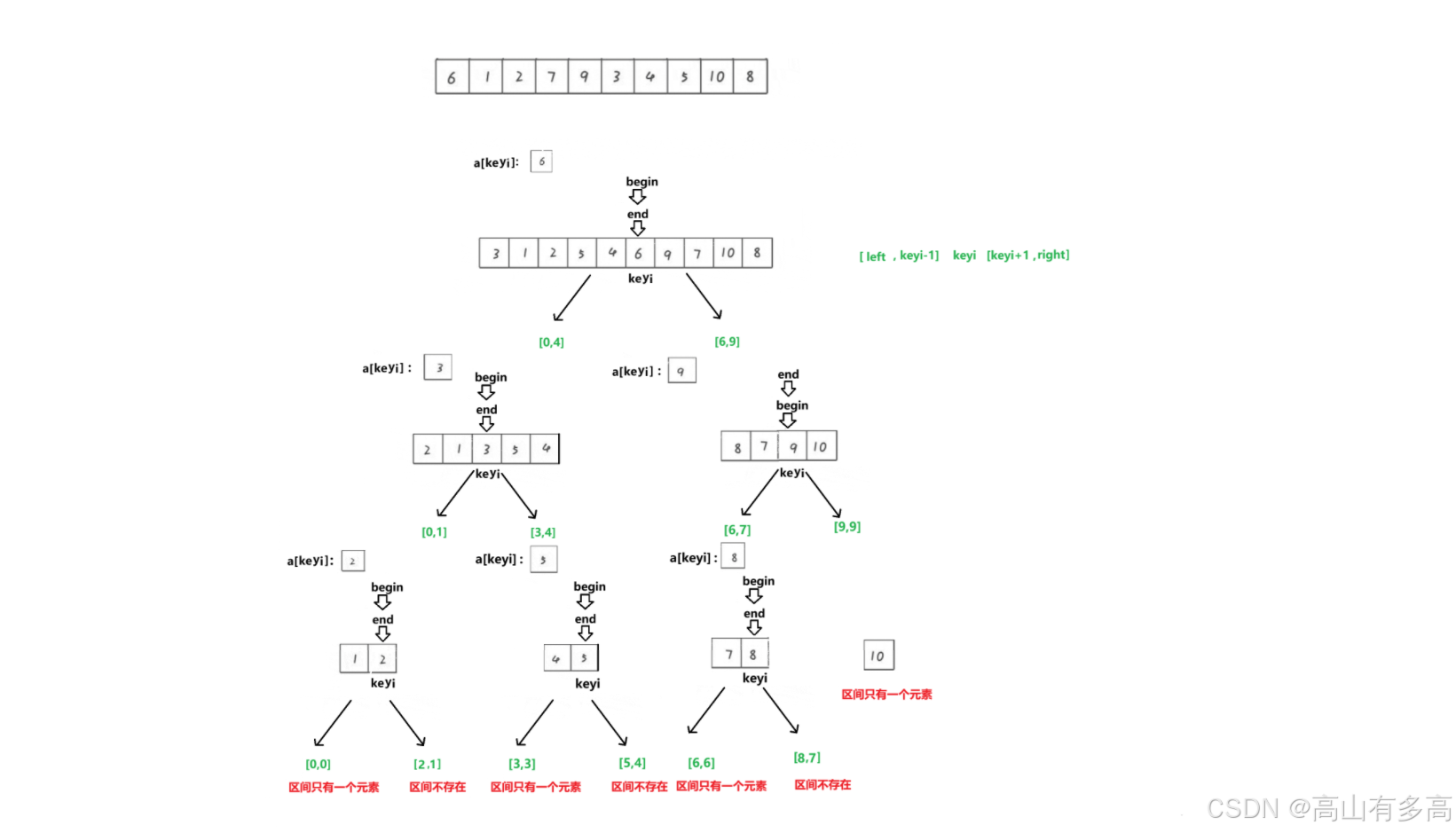
三、代码实现

#include <iostream>
#include <stack>
#include <vector>
#include <algorithm> 

using namespace std;

// 1. 实现快慢指针法分区 (PartitionSlowFast)
// prev 是慢指针，cur 是快指针
int PartitionSlowFast(int* a, int left, int right)
{
    int keyi = left; // 选取最左边为 key 的下标
    int prev = left;
    int cur = left + 1;

    while (cur <= right) 
    {
        // 如果快指针指向的值小于 key，且 prev 下一步不是 cur 自己
        // prev 前进一步，并交换 prev 和 cur 的值
        if (a[cur] < a[keyi]&& ++prev!=cur) 
        {
           swap(a[prev], a[cur]);
        }
        cur++;
    }
    
    // 最后将 key 放到 prev 的位置
    swap(a[keyi], a[prev]);
    return prev; // 返回 key 最终的位置
}

// 2. 非递归快速排序主函数
void QuickSortNonR(int* a, int left, int right)
{

    stack<int> st;

    // 初始状态入栈：注意栈是后进先出
    // 我们希望出来的时候先拿 begin，再拿 end
    // 所以先压入 right (end)，再压入 left (begin)
    if (left < right)
    {
        st.push(right);
        st.push(left);
    }

    while (!st.empty())
    {
        // 取栈顶元素
        int begin = st.top();
        st.pop();

        int end = st.top();
        st.pop();

        // 使用快慢指针法进行一趟分割
        int keyi = PartitionSlowFast(a, begin, end);

        // [begin, keyi-1] keyi [keyi+1, end]

        // 核心逻辑保持不变：先处理右边，再处理左边（为了模拟递归顺序）
        // 也就是先压入右区间，再压入左区间

        // 处理右区间 [keyi+1, end]
        int left2 = keyi + 1;
        int right2 = end;
        
        //区间只有一个元素不入栈，区间不存在也不入栈
        if (right2 - left2 >=1)
        {
            st.push(right2); 
            st.push(left2);  
        }

        // 处理左区间 [begin, keyi-1]
        int left1 = begin;
        int right1 = keyi - 1;

        if (right1 - left1>=1)
        {
            st.push(right1); 
            st.push(left1);  
        }
    }

}