排序算法指南：计数排序

原创已于 2025-12-12 20:03:35 修改 · 1.4k 阅读

53 ·

CC 4.0 BY-SA版权

文章标签：

#排序算法 #算法 #c++ #开发语言 #c语言 #数据结构

于 2025-12-10 20:32:55 首次发布

数据结构与算法专栏收录该内容

25 篇文章

订阅专栏

前言：

计数排序（Counting Sort）是一种非比较型的排序算法，它的核心思想是利用数组来存储输入数据中每个元素的出现次数，然后根据这些统计信息来确定输出序列。

一、计数排序的原理

计数排序适用于整数数据，且这些整数的范围不宜过大，它的基本步骤如下：

①找出范围：确定输入数组中最大值（max）和最小值（min），从而确定数据的范围range：max-min+1

②创建计数数组：创建一个长度为 range 的计数数组 count，用于存储输入数组 a 中每个元素的出现次数。

③统计次数：遍历输入数组 a，将每个元素的值作为索引，在计数数组 count 对应位置进行计数

如果输入数组 a中包含负数，直接使用元素的值作为计数数组 count 的索引会导致程序错误，因为数组索引不能为负



解决方案：解决这个问题的通用方法是引入一个偏移量（Offset），将所有数据映射到一个非负的索引范围。

1. 确定最小负值



首先，遍历输入数组a，找出其中的最小值min。



2. 计算偏移量



如果 min是负数（例如 min = -5），那么这个min 的绝对值 |min| 就是我们需要的偏移量offest 。



offest = -min



3. 映射到非负索引



对于输入数组 a 中的任意元素 a[i]，它在计数数组 count 中的对应索引 index 应该计算为：index = a[i] + offset



这样，即使 a[i] 是负数，例如 A[i]=-5，index 就会是 -5 + 5 = 0，保证了索引的非负性。





例：数组a为：  [-5, 3, -1, 0, 3, -5]



最小值min = -5



最大值max = 3



偏移量offset = -(-5) = 5



a[0]= -5 ---> 映射到count数组的下标为： -5+5=0



a[1]= 3 ---> 映射到count数组的下标为： 3+5=8



a[2]= -1 ---> 映射到count数组的下标为： -1+5=4



a[3]= 0 ---> 映射到count数组的下标为： 0+5=5



a[4] = 3 ---> 映射到count数组的下标为： 3+5=8



a[5] = -5  ---> 映射到count数组的下标为： -5+5=0

④计算累计次数：计算数组中元素的出现个数：count[a[i]+min]++

⑤输出排序数组: 遍历整个计数数组，将每个索引位置的值作为元素出现的次数，依次将该索引对应的元素输出到结果数组中。

例：数组a为：  [-5, 3, -1, 0, 3, -5]



最小值min = -5



最大值max = 3



偏移量offset = -(-5) = 5



count数组为：[2,0,0,0,1,1,0,0,2]



温馨提示：由于偏移量的问题，所以在C数组对应的索引需要进行加上偏移量后输出到结果数组



例如： count[0] = 2, 表示的是 a[i]-offset 出现了2次

二、计数排序的工作流程

以如下数组为例，数组a[2 3 8 7 1 2 2 2 7 3 9 8 2 1 4 2 4 6 9 2]

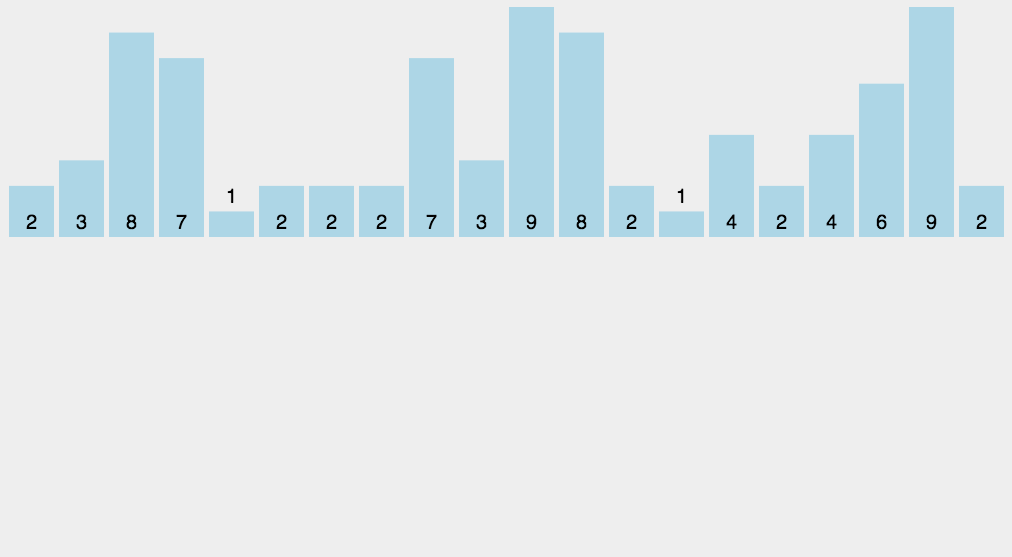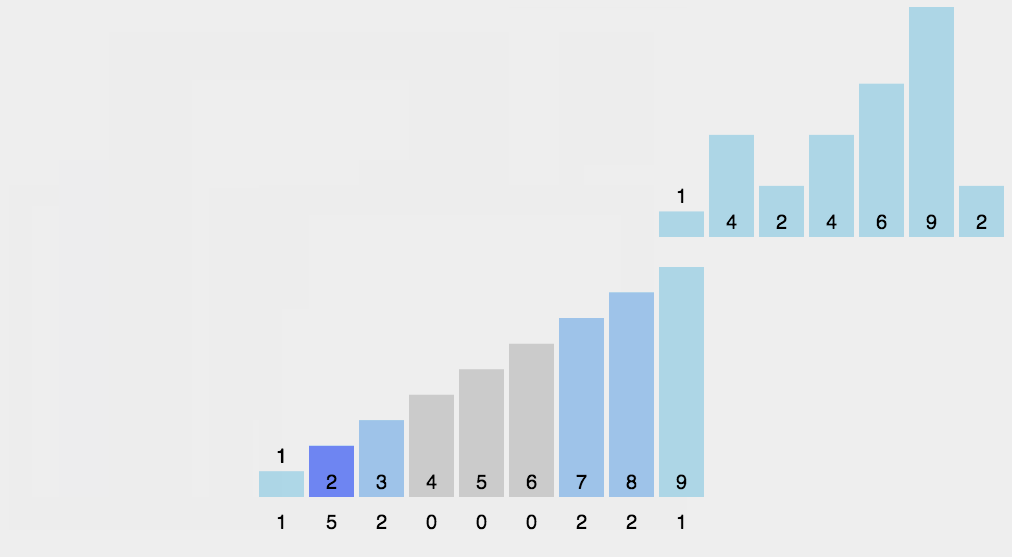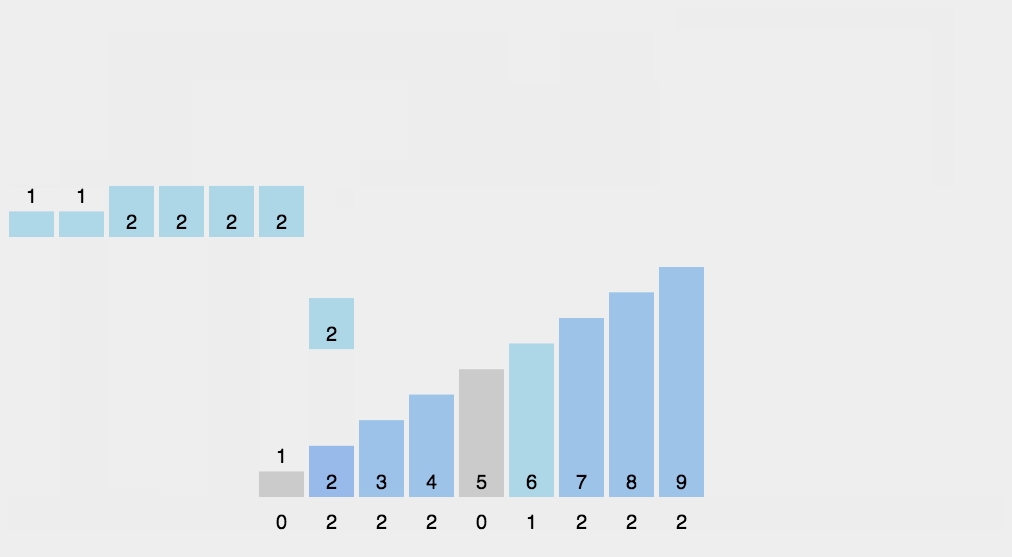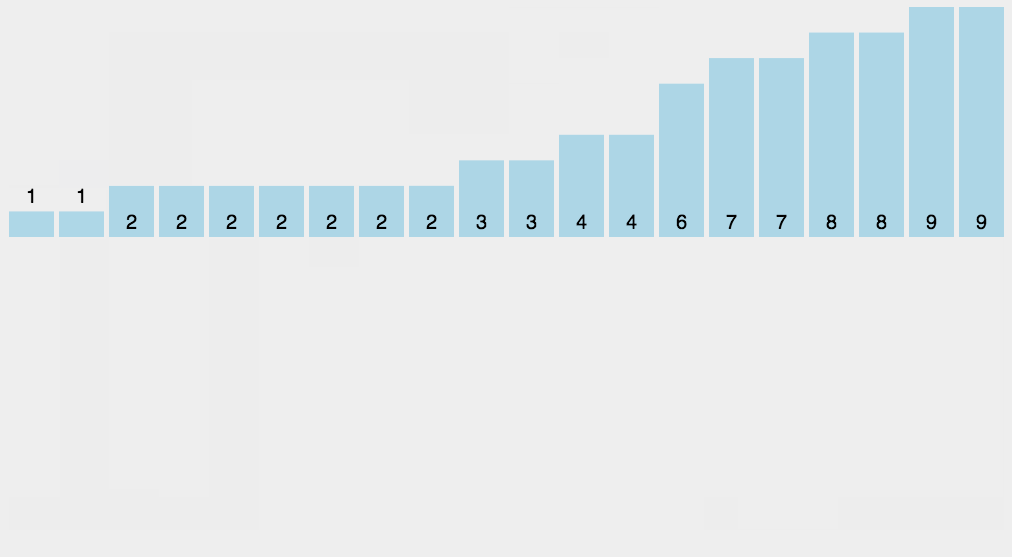
第一步：找到 min、max

扫描数组：



min = 1



max = 9



range=max - min + 1 也就是 count 数组长度 = 9

第二步：统计出现次数

从 0 到 n-1 依次扫描每个数字

数组a	数字	下标 = 数字-min	count 更新
a[0]	2	1	count[1] = 1
a[1]	3	2	count[2] = 1
a[2]	8	7	count[7] = 1
a[3]	7	6	count[6] = 1
a[4]	1	0	count[0] = 1
a[5]	2	1	count[1] = 2
a[6]	2	1	count[1] = 3
a[7]	2	1	count[1] = 4
a[8]	7	6	count[6] = 2
a[9]	3	2	count[2] = 2
a[10]	9	8	count[8] = 1
a[11]	8	7	count[7] = 2
a[12]	2	1	count[1] = 5
a[13]	1	0	count[0] = 2
a[14]	4	3	count[3] = 1
a[16]	2	1	count[1] = 6
a[17]	4	3	count[3] = 2
a[18]	6	5	count[5] = 1
a[19]	9	8	count[8] = 2
a[20]	2	1	count[1] = 7

第三步：倒出排序结果

从 0 到 range-1 依次扫描每个数字,根据索引中的次数，添加元素到数组a中

数字	出现次数	写入结果	当前数组a
1	2	写 1 两次到数组a	[1,1]
2	7	写 2 七次到数组a	[1,1,2,2,2,2,2,2,2]
3	2	写 3 两次到数组a	[1,1,2,2,2,2,2,2,2,3,3]
4	2	写 4 两次到数组a	[1,1,2,2,2,2,2,2,2,3,3,4,4]
6	1	写 6 一次到数组a	[1,1,2,2,2,2,2,2,2,3,3,4,4,6]
7	2	写 7 两次到数组a	[1,1,2,2,2,2,2,2,2,3,3,4,4,6,7,7]
8	2	写 8 两次到数组a	[1,1,2,2,2,2,2,2,2,3,3,4,4,6,7,7,8,8]
9	2	写 9 两次到数组a	[1,1,2,2,2,2,2,2,2,3,3,4,4,6,7,7,8,8,9,9]

三、代码示例

void CountSort(int *a,int n)
{
	int min = a[0], max = a[0];
	for (int i = 0; i < n; i++)
	{
		if (a[i] > max)max = a[i];
		if (a[i] < min)min = a[i];
	}

	//开辟数组的大小
	int range = max - min + 1;
	
	//创建一个数组：记录每个数的出现个数
	int* count = (int *)calloc(sizeof(int) ,sizeof( int ) * range);
	
	if (count == NULL)
	{
		perror("calloc fail\n");
		return;
	}

	//根据相对偏移量
	for (int i = 0; i < n; i++)
	{
		count[a[i] - min]++;
	}

	//定义一个临时数组当前的下标
	int j = 0;
	for (int i = 0; i < range; i++)
	{
		while (count[i]--)
		{
			a[j++] = i + min;
		}
	}

}

四、复杂度分析

4.1时间复杂度

计数排序主要分 3 步：

1. 找最小值与最大值

	int min = a[0], max = a[0];
	for (int i = 0; i < n; i++)
	{
		if (a[i] > max)max = a[i];
		if (a[i] < min)min = a[i];
	}

遍历一遍数组 O(n)

2. 建计数数组并统计每个数字出现次数

	//根据相对偏移量
	for (int i = 0; i < n; i++)
	{
		count[a[i] - min]++;
	}

遍历一次数组 O(n)

3. 倒出排序结果

	//定义一个临时数组当前的下标
	int j = 0;
	for (int i = 0; i < range; i++)
	{
		while (count[i]--)
		{
			a[j++] = i + min;
		}
	}

最坏情况下 O(n + range)

⭐ 总时间复杂度

O(n) + O(n) + O(n + range) = O(n + range)

4.2空间复杂度

	//开辟数组的大小
	int range = max - min + 1;
	
	//创建一个数组：记录每个数的出现个数
	int* count = (int *)calloc(sizeof(int) ,sizeof( int ) * range);
	
	if (count == NULL)
	{
		perror("calloc fail\n");
		return;
	}

开辟一个大小为range的数组，空间复杂度为O（range）

既然看到这里了，不妨关注+点赞+收藏，感谢大家，若有问题请指正。