排序算法指南：冒泡排序

原创于 2025-11-30 15:31:27 发布 · 556 阅读

16 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构 #c语言 #开发语言 #算法 #c++

前言：

冒泡排序（Bubble Sort）是一种简单直观的排序算法。其核心原理是通过相邻元素的反复比较和交换，使较大元素逐渐"上浮"到序列末端，较小元素自然"下沉"到前端，最终实现整个序列的有序排列。

冒泡排序作为我们接触的第一个排序算法，尽管实际应用中因其效率较低而较少采用，但它为理解排序算法的核心思想奠定了重要基础，对于任何排序算法，我们都可以采用从局部到整体的思维，先排好一趟元素，再进行全部元素的排序。

一、冒泡思想的介绍

为什么叫“冒泡”排序？

想象一下你有一瓶雪碧。气泡（大的元素）会不断地往上冒，直到浮到水面（数组末尾）。

核心操作：两两元素进行比较，相邻之间交换

效果：每一轮循环结束，当前最大的那个数，就会像气泡一样，“漂”到了数组的最右边。

二、冒泡排序的工作原理

以排列升序元素为例，工作原理如下：

初始化：从数组的第一个元素开始，逐一比较相邻的元素。



比较和交换：如果当前元素比下一个元素大，则交换这两个元素的位置。



冒泡过程：每一轮遍历后，未排序部分的最大元素会被移到该部分的末尾（类似于气泡浮起的过程）。



重复遍历：继续对未排序部分进行相同的操作，每次遍历都会减少一个已排序的元素。

如下动图所示：

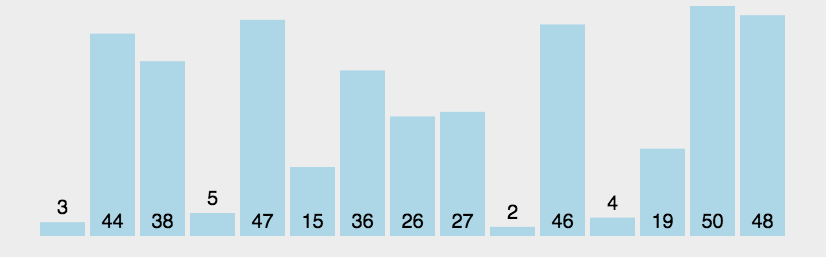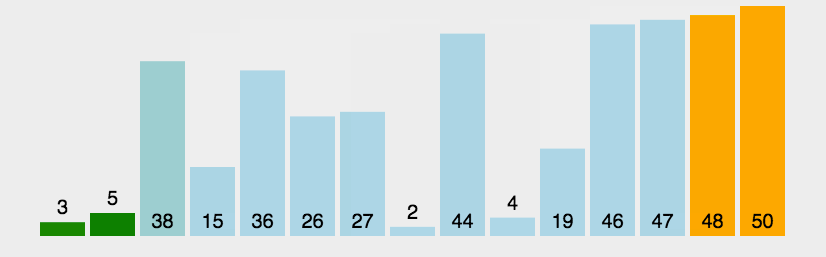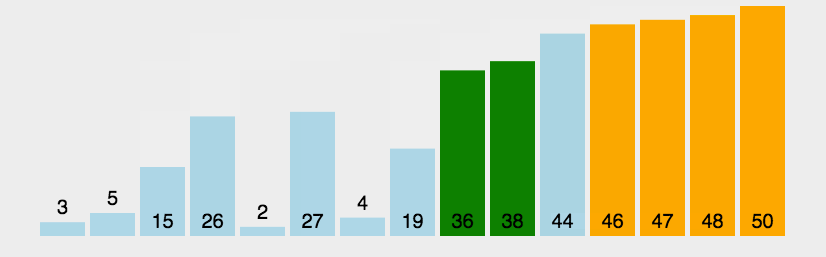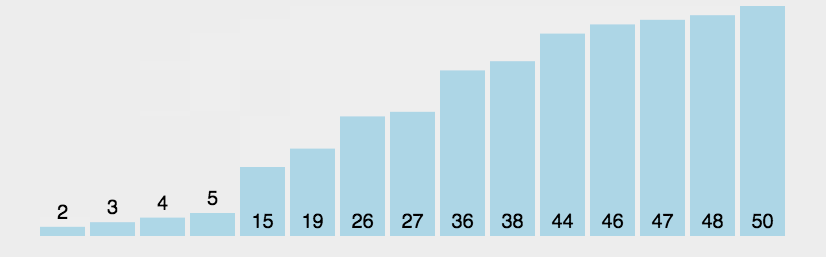
三、冒泡排序的实现

以上述数组为例，假设有一个待排列的数组为：[3，44，38，5，47，15，36，26，27，2，46，4，19，50，48]。

第一趟遍历：

比较 3 和 44，3 < 44，不交换。



比较 44 和 38，44 > 38，交换：[3, 38, 44, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]



比较 44 和 5，44 > 5，交换：[3, 38, 5, 44, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]



比较 44 和 47，44 < 47，不交换。



比较 47 和 15，47 > 15，交换：[3, 38, 5, 44, 15, 47, 36, 26, 27, 2, 46, 4, 19, 50, 48]



比较 47 和 36，47 > 36，交换：[3, 38, 5, 44, 15, 36, 47, 26, 27, 2, 46, 4, 19, 50, 48]



比较 47 和 26，47 > 26，交换：[3, 38, 5, 44, 15, 36, 26, 47, 27, 2, 46, 4, 19, 50, 48]



比较 47 和 27，47 > 27，交换：[3, 38, 5, 44, 15, 36, 26, 27, 47, 2, 46, 4, 19, 50, 48]



比较 47 和 2，47 > 2，交换：[3, 38, 5, 44, 15, 36, 26, 27, 2, 47, 46, 4, 19, 50, 48]



比较 47 和 46，47 > 46，交换：[3, 38, 5, 44, 15, 36, 26, 27, 2, 46, 47, 4, 19, 50, 48]



比较 47 和 4，47 > 4，交换：[3, 38, 5, 44, 15, 36, 26, 27, 2, 46, 4, 47, 19, 50, 48]



比较 47 和 19，47 > 19，交换：[3, 38, 5, 44, 15, 36, 26, 27, 2, 46, 4, 19, 47, 50, 48]



比较 47 和 50，47 < 50，不交换。



比较 50 和 48，50 > 48，交换：[3, 38, 5, 44, 15, 36, 26, 27, 2, 46, 4, 19, 47, 48, 50]



此时，最大的元素 50 已经“冒泡”到数组的末端。

由一趟排序我们可以得到如下代码：

	//排序一趟
    //j控制的是每趟需要排序元素的比较次数
	for (int j = 0; j < n - 1; j++)
	{
		if (a[j] > a[j + 1])
		{
			Swap(&a[j], &a[j + 1]);
		}
	}

对于冒泡排序来说，通常来说，经过 n-1 趟排序就足够了，因为在第 n-1 趟结束后，最后一个元素已经排好序，不再需要再参与排序。

解释：



第一轮遍历：比较相邻元素，最大值会“冒泡”到数组的末尾。



第二轮遍历：比较相邻元素，第二大的值会“冒泡”到倒数第二的位置。



以此类推...



所以，经过 n-1 趟之后，最后一个元素就已经是排序好的最大元素，不再需要参与接下来的排序。

故而对n个元素进行排序的代码如下，只需要再添加一层循环控制排序的趟数：

void BubbleSort(int* a, int n)
{
	//i控制的是排序的趟数
	for (int i = 0; i < n - 1; i++)
	{
		//排序一趟
		//j控制的是每趟需要排序元素的比较次数
        //每排一趟，需要排序需要排序的元素少一个
		for (int j = 0; j < n - 1- i; j++)
		{
			if (a[j] > a[j + 1])
			{
				Swap(&a[j], &a[j + 1]);
			}
		}

	}

}

四、冒泡排序的优化

对于已经有序数组，冒泡排序的优化

在标准冒泡排序的实现中，每一趟排序都会遍历整个数组，将相邻的元素进行比较和交换。

然而，对于已经有序的数组，比较操作会发现没有元素需要交换，这意味着每一趟遍历并不会发生交换。

所以我们可以通过添加标记，判断是否一趟排序有元素交换，如果没有则说明已经是有序数组，如果有则说明还要进行排序。

void BubbleSort(int* a, int n)
{
	
	//i控制的是排序的趟数
	for (int i = 0; i < n - 1; i++)
	{
        //定义一个标记,默认为0
		int flag = 0;
		//排序一趟
		//j控制的是每趟需要排序元素的比较次数
        //每排一趟，需要排序需要排序的元素少一个
		for (int j = 0; j < n - 1- i; j++)
		{
			if (a[j] > a[j + 1])
			{
				Swap(&a[j], &a[j + 1]);
                //出现交换，标记变为1
				flag = 1;
			}
		}
        
		if (!flag) break;
	}

}

五、冒泡排序时空复杂度的分析

1.时间复杂度分析

1.1最坏情况：O(n²)

在最坏的情况下（例如，输入数组是完全逆序的），冒泡排序会进行 n-1 趟排序



每一趟都需要进行 n-i-1 次相邻元素的比较和交换（i 是当前的遍历轮数）。



第 1 轮遍历：需要比较和交换 n-1 次



第 2 轮遍历：需要比较和交换 n-2 次



...



第 n-1 轮遍历：需要比较和交换 1 次



因此，总的比较次数为（等差数列求和）：



(n−1)+(n−2)+⋯+2+1=(1 + n - 1 ) * (n - 1) / 2



最坏情况时间复杂度：O(n²)

1.2 最好情况：O(n)

在最好情况下，即数组已经有序时，冒泡排序依然会遍历一遍整个数组，但没有发生任何交换。



在优化版本的冒泡排序中，如果某一趟遍历没有发生交换，算法会提前终止。



这时，算法只会进行一次遍历，比较每一对相邻元素，但没有发生交换。由于没有交换，排序会在第一次遍历结束后提前终止。



最好情况时间复杂度：O(n)