前言:
插入排序(Insertion Sort)是一种简单直观的排序算法。它的基本思想是:将数组分为已排序区间和未排序区间,逐步从未排序区间取出元素并插入到已排序区间的正确位置,直到所有元素都排序完成。

一、插入排序的思想
以打扑克牌的场景为例:假设你手中已经有一些按顺序排列的牌。当你摸到一张新牌时,你会如何将它插入到正确的位置?
①你会从右往左看手里已经排好的牌。
②找到这张新牌应该插入的位置。
③把它插进去,这样手里的牌依然是积有序的。
这就是插入排序的核心思想!
如下图所示:排列升序数组 [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]
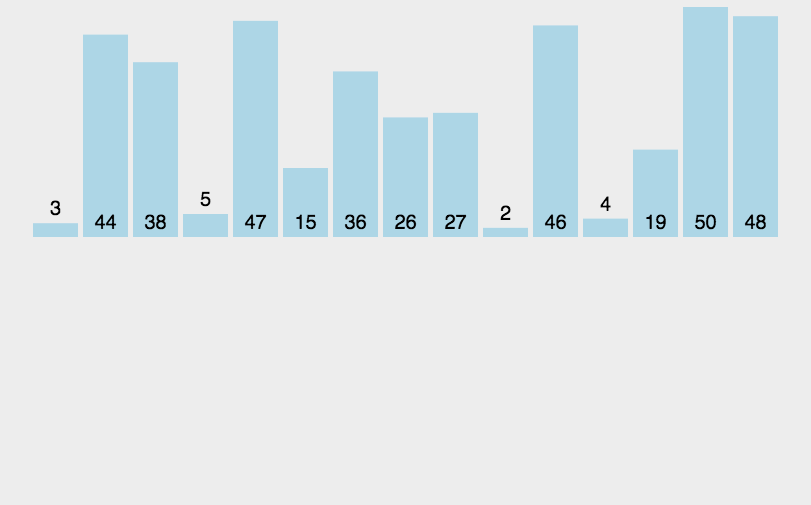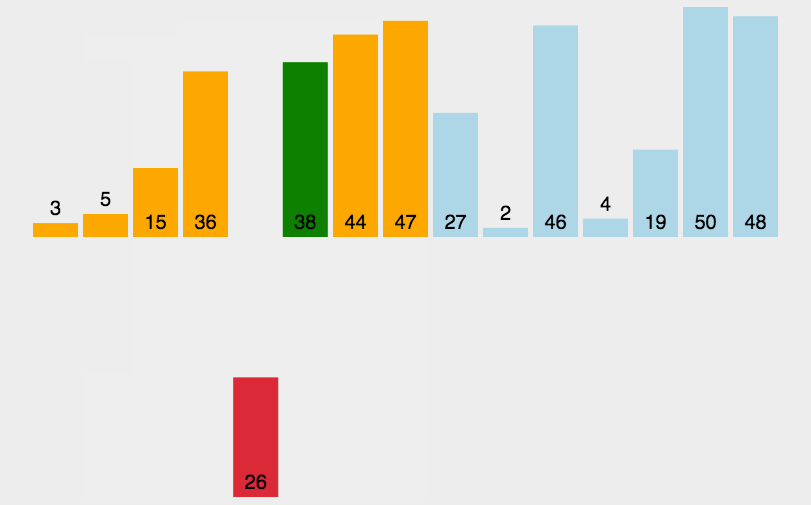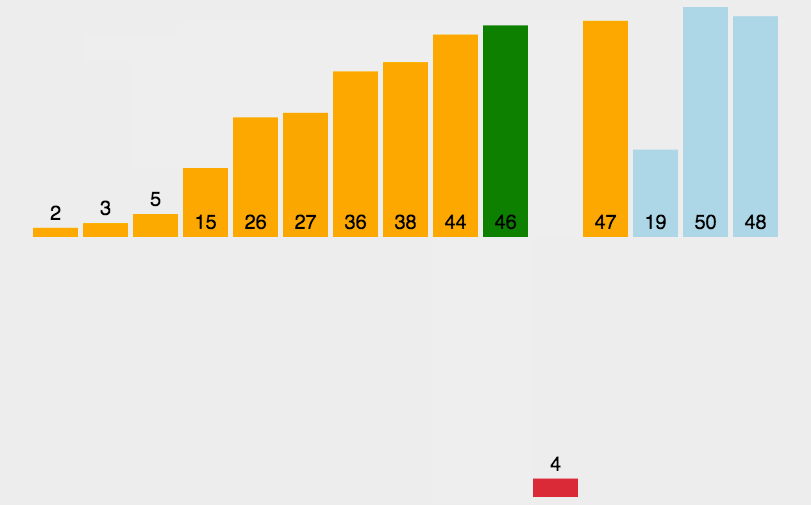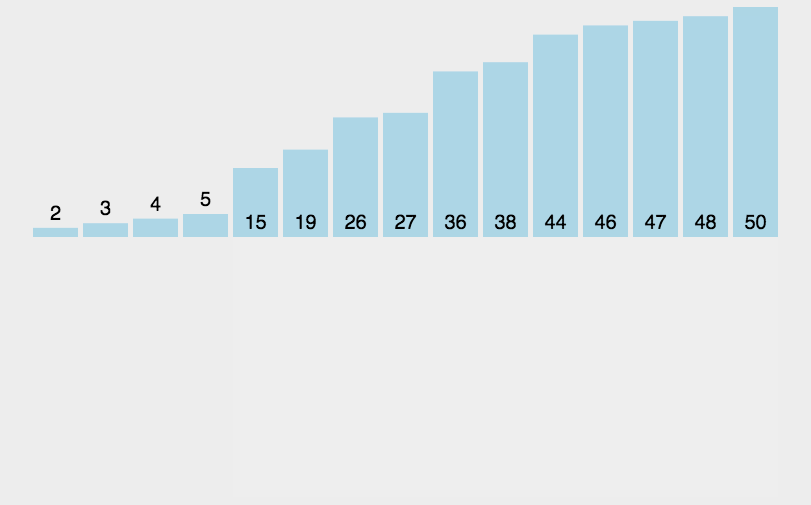
二、插入排序的工作原理
假设我们要对一个待排序数组 A 进行排序,步骤如下:
①初始状态:我们认为数组的第一个元素(下标索引为0)已经是排好序的
②取新元素:从第二个元素(下标索引为1),将其作为“待插入的元素”(我们用tmp变量来存储)
③比较与移动:拿tmp与它左边的元素进行比较
1. 如果左边的元素比tmp的值大,就把它向右移动一位(给tmp腾出一个空位)
2.继续向左比较,直到找到一个比 tmp 小的元素,或者已经到了数组的最左边
④插入:把tmp放入刚才腾出的空位中。
⑤重复:对数组中的下一个元素重复上述步骤,直到排列完最后一个元素。
以图示数组为例,用文字版讲解插入排序的详细过程:[3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]
1. 初始状态
有序区:
[3](第一个元素总是默认有序)待排区:
[44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]
2. 处理
44(索引 1)
tmp
= 44比较3和44:
44和有序区的最后一个元素3比较。
44 > 3,不需要移动3,将tmp=44直接插入到3的后面。
当前数组状态:
[3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]有序区:
[3, 44]
3. 处理
38(索引 2)
tmp
= 38
38 < 44:44比 38 大,所以44向右移动一位(到索引 2 的位置)。数组临时变成:
[3, 44, 44,5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48](想象44移了位置)继续比较
38和下一个有序区元素3。
38 > 3:38比3大,停止移动,38应该插入到3的后面。
当前数组状态:
[3, 38, 44, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]有序区:
[3, 38, 44]
4. 处理
5(索引 3) 关键的一步!
tmp = 5比较
5和44:5 < 44,44向右移。数组临时:
[3, 38, 44, 44, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]比较
5和38:5 < 38,38向右移。数组临时:
[3, 38, 38, 44, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]比较
5和3:此时5 > 3,停止比较。5应该插入到3的后面。
当前数组状态:
[3, 5, 38, 44, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]有序区:
[3, 5, 38, 44, 47]
5. 处理
47(索引 4)
tmp = 47比较
47和47:此时47和47相等,不进行移动,47直接插在47后面(也就是它自己的位置)。
当前数组状态:
[3, 5, 38, 44, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]有序区:
[3, 5, 38, 44, 47]
6. 处理
15(索引 5)
tmp = 15
15 < 47->47向右移
15 < 44->44向右移
15 < 38->38向右移
15 > 5-> 停,将tmp=15插入到5后面。
当前数组状态:
[3, 5, 15, 38, 44, 47, 36, 26, 27, 2, 46, 4, 19, 50, 48]有序区:
[3, 5, 15, 38, 44, 47]
7. 处理
36(索引 6)
tmp = 36
36会依次和47,44,38比较,然后插入到15后面。
当前数组状态:
[3, 5, 15, 36, 38, 44, 47, 26, 27, 2, 46, 4, 19, 50, 48]有序区:
[3, 5, 15, 36, 38, 44, 47]
8. 处理
26(索引 7)
tmp = 26
26会和47, 44, 38, 36比较,然后插入到15后面。
当前数组状态:
[3, 5, 15, 26, 36, 38, 44, 47, 27, 2, 46, 4, 19, 50, 48]有序区:
[3, 5, 15, 26, 36, 38, 44, 47]
9. 处理
27(索引 8)
tmp = 27
27会和47, 44, 38, 36, 26比较,然后插入到26后面。
当前数组状态:
[3, 5, 15, 26, 27, 36, 38, 44, 47, 2, 46, 4, 19, 50, 48]有序区:
[3, 5, 15, 26, 27, 36, 38, 44, 47]
10. 处理
2(索引 9) 🚀 全场最小的出现!
tmp = 2
2遇到了47,由于2 < 47,47向右移!
2遇到了44,由于2 < 44,44向右移!
2遇到了38,由于2 < 38,38向右移!
2遇到了27,由于2 < 27,27向右移!
2遇到了26,由于2 < 26,26向右移!
2遇到了15,由于2 < 15,15向右移!
2遇到了5,由于2 < 5,5向右移!
2遇到了3,由于2 < 3,3向右移!现在到了有序区的最左边(索引 0),
2比前面的所有数都小。2插入到最前面!
当前数组状态:
[2, 3, 5, 15, 26, 27, 36, 38, 44, 47, 46, 4, 19, 50, 48]有序区:
[2, 3, 5, 15, 26, 27, 36, 38, 44, 47]
11. 处理
46(索引 10)
tmp = 46
46会和47比较,46 < 47,47移。
46和44比较,46 > 44,停止。插入到44后面。
当前数组状态:
[2, 3, 5, 15, 26, 27, 36, 38, 44, 46, 47, 4, 19, 50, 48]有序区:
[2, 3, 5, 15, 26, 27, 36, 38, 44, 46, 47]
12. 处理
4(索引 11)
tmp = 4
4会和47, 46, 44, 38, 36, 27, 26, 15依次比较并移动,最后插入到5后面。
当前数组状态:
[2, 3, 4, 5, 15, 26, 27, 36, 38, 44, 46, 47, 19, 50, 48]有序区:
[2, 3, 4, 5, 15, 26, 27, 36, 38, 44, 46, 47]
13. 处理
19(索引 12)
tmp = 19
19会和47, 46, 44, 38, 36, 27, 26比较并移动,插入到15后面。
当前数组状态:
[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 50, 48]有序区:
[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47]
14. 处理
50(索引 13)
tmp = 50
50 > 47,直接插入到47后面。
当前数组状态:
[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 50, 48]有序区:
[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 50]
15. 处理
48(索引 14)
tmp = 48
48 < 50,50移。
48 > 47,停止。插入到47后面。
当前数组状态:
[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]有序区:
[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
三、插入排序的实现
通过上述模拟排序过程,我们已能掌握插入排序的工作原理和实现思路。实际上,任何排序算法都可以从单趟排序出发,遵循由局部到整体的思考方式。
void InsertSort(int* a, int n)
{
//比较下标[0,end]的值,将a[end+1]插入到[0,end]中
//若待排列数组有n个元素,下标end的最大取值n-2,最小取值为0
for (int i = 0; i < n - 1; i++)
{
int end=i;
int tmp = a[end + 1];
while (end >= 0)
{
if (tmp < a[end])
{
//将a[end]往后挪动
a[end + 1] = a[end];
//调整end的值,继续向前寻找
end--;
}
else
{
//如果出现a[end+1]>=a[end],说明end+1找到位置
break;
}
}
//对于退出循环有两种情况
//情况一:因为break而退出,a[end+1]>=a[end]
//情况二:因为查找完[0,end]的值仍是最小,此时end=-1,此时a[end+1]为a[0]
a[end + 1] = tmp;
}
}
温馨提示:
这里有两个关键:
关键点一:假设需要排列n个元素的数组,则end下标最大值只能是n-2,即end的范围为[0,n-2]
对于这部分的理解可以抽象为打扑克牌时,end可以认为是手上最后一张牌的下标,end+1是刚从牌堆中摸的一张牌,需要插入到手中的牌中,而最后一张摸的牌下标为n-1,所以此时手中end的下标最大为n-2。
关键点二: 对于退出while循环有两种情况
情况一:因为break而退出,a[end+1]>=a[end]
情况二:因为查找完[0,end]的值仍是最小,此时end=-1,此时a[end+1]为a[0]
四、插入排序的时间复杂度
1. 最优情况(Best Case)
最优情况发生在输入数据已经是有序的情况下,插入排序的算法会一次遍历所有元素,不需要进行任何交换或移动。
每次插入操作的比较次数都是常数级别的,因此总体的时间复杂度是 O(n)。
2.最坏情况(Worst Case)
最坏情况发生在输入数据是反向排序的情况下(即逆序排列)。
在这种情况下,每个元素都需要与之前所有已排序的元素进行比较,因此每次插入操作的比较次数是逐步增加的。
第一个元素需要与前面0个元素比较,第二个元素需要与1个元素比较,第三个需要与2个元素比较,... ... 第n个元素需要与n-1个元素进行比较
故而需要比较的次数为T(n)= 0 + 1 + 2 + ... ... + n-1 = (n-1) * n /2
因此,总体的时间复杂度是 O(n^2)
五、插入排序的缺陷
1. 数据量大时,效率极低
这是它最大的硬伤:插入排序的时间复杂度是O(n^2) ,这意味着,如果数据量增加 10 倍,耗费的时间可能会增加 100 倍!
举个栗子:
排 10 个数字,可能只要 0.0001 秒。
排 10,000 个数字,可能需要几秒。
排 1,000,000 (一百万) 个数字,可能需要几天甚至几周!
2.数据移动非常频繁
我们在之前的步骤里看到了,每次插入一个比前面小的数字,后面的所有数字都要往后挪一位。
最坏情况:如果数组是完全倒序的(比如我们要从小到大排,但数组是
[10, 9, 8, ..., 1])。
后果:每一个新元素插入,都要把前面所有排好的元素全部移动一遍。
代价:在计算机中,“写入”内存的操作比单纯的“比较”操作要慢,如果你排序的是复杂的对象(比如一个很大的结构体),频繁地搬运它们会消耗大量的性能。
3. 对“逆序”数据非常敏感
插入排序的性能极度依赖于数据的初始状态。如果数据本来就是乱的,或者倒序的,它的表现会非常差。
①它缺乏一种“跳跃式”的调整能力,它只能一步一步地挪动元素。
②如果一个很小的数字在数组的最后面(比如上述数组中的 2,一开始在索引 9),它必须经过无数次比较和移动,才能像蜗牛一样爬到最前面。
既然插入排序最大的痛点是:“一次只能移动一步”(导致小的数字要很久才能移到前面),那有没有办法让它“一次迈大步” 进行交换呢?
这就要引出shell排序了,欲知后事如何,请听下回分解。
既然看到这里了,不妨关注+点赞+收藏,感谢大家,若有问题请指正。























 787
787

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








