DFS和BFS其实学的很早,但是DFS我一直很菜

题目链接:洛谷P1219 传送门

众所周知(In my opinion),八皇后是学DFS必刷的题,然而,本蒟蒻到今天才写。
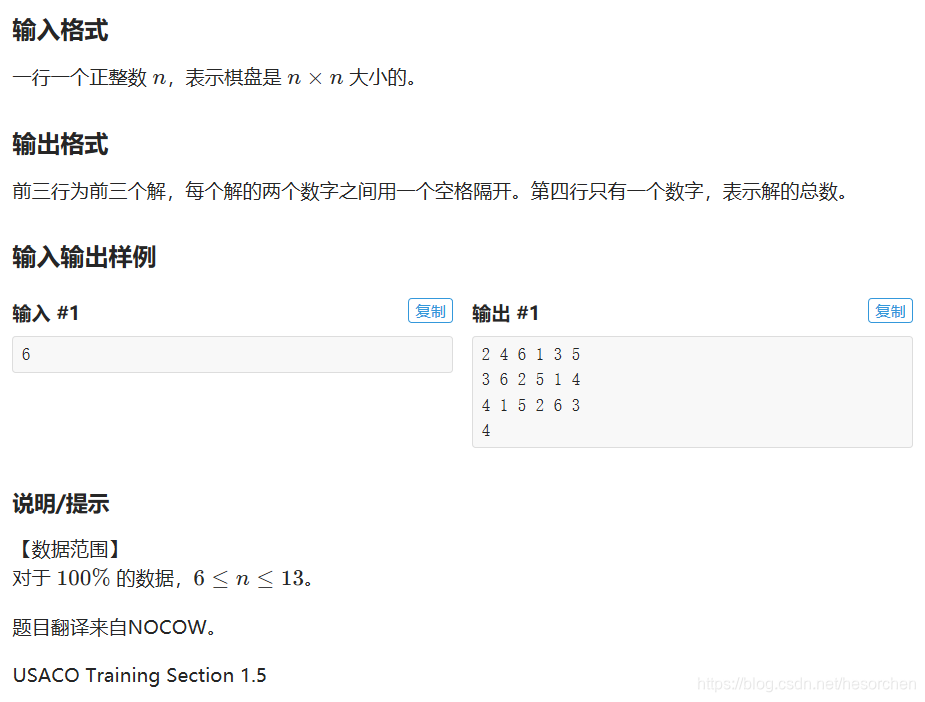
题目很简单,就是经典八皇后,只不过让你输出字典序最小的三个解,然后再输出总共有几种解。
很简单,我们开四个数组a,b,c,d分别用来记录行、列、左上到右下,右下到左上这四种方向上皇后的占领情况,由题意,a数组直接记录该行皇后的位置,其他三个数组只需标记即可
代码:
#include <stdio.h>
#include <cstring>
#include <iostream>
#include <string>
#include <cmath>
#include <algorithm>
#include <cstdlib>
#include <queue>
#include <deque>
#include <cstring>
#include <iterator>
#include <set>
#include <map>
using namespace std;
#define ll long long
int a[100], b[100], c[100], d[100];
//分别表示行、列、左上到右下,左下到右上的皇后占领情况
int n;
int ans;
void print()
{
if (ans < 3)//输出前三个解
{
printf("%d", a[1]);
for (int i = 2; i <= n; i++)
printf(" %d", a[i]);
cout << endl;
}
ans++;
}
void queen(int x)
{
if (x > n)
{
print();
return;
}
for (int i = 1; i <= n; i++)
{
if ((!b[i]) && (!c[n + x - i]) && (!d[i + x - 1]))
//如果该位置未被占领
{
b[i] = 1;
c[n + x - i] = 1;
d[i + x - 1] = 1;
a[x] = i;
queen(x + 1);
b[i] = 0;
c[n + x - i] = 0;
d[i + x - 1] = 0;
}
}
}
int main()
{
cin >> n;
queen(1);
cout << ans << endl;
return 0;
}
























 1815
1815












