石墨烯开关晶体管设计

用于垂直电路设计的石墨烯开关晶体管

摘要

提出了一种基于石墨烯‐六方氮化硼（hBN）‐石墨烯垂直异质结构的石墨烯开关晶体管（GST）。源极和漏极之间的载流子输运由上下石墨烯层通过三层hBN的垂直层间隧穿引起的沟道中费米能级移动所控制。推导了解析电流输运方程，并研究了其特性。该GST在0.1 V电源电压下工作时，具有2.97毫伏每十倍频程的陡峭亚阈值斜率，以及2.45 × 10⁴的开关电流比。对于有效沟道面积为0.05 μm²的情况，估计驱动电流为 88 μA/μm²。还研究了基于GST的垂直反相器的电压传输特性，发现其在关到开状态之间具有陡峭转换特性。与预测的2020年nMOSFET相比，GST的动态功耗降低了15倍，关态漏电功耗降低了194倍。

引言

金属半导体场效应晶体管（MOSFET）的尺寸缩放预计将 达到其基本物理极限，因为摩尔定律在每个技术节点上越来越 难以维持。国际半导体技术路线图（ITRS）列出了若干种非 经典新兴器件，作为传统基于硅的MOSFET的潜在替代方案。在此背景下，ITRS不仅指新型器件结构，还包括基于其他新型非经典材料的器件。原子级厚度的二维石墨烯因其独特的电子特性，已成为下一代电子器件的潜在候选材料。然而，单层石墨烯是一种零带隙半导体。由于缺乏带隙，石墨烯场效应晶体管的开关电流比差，且关态漏电流较高。根据国际半导体技术路线图（ITRS）对高能效电路设计的要求，在电源电压低于0.7 V时，数字应用所需的开关电流比为10⁴。现有基于石墨烯的MOS型晶体管的性能仍落后于要求。

为了解决开关所需的电流比问题，已提出使用由多层堆叠的石墨烯和其他原子级薄二维材料（如氮化硼和过渡金属二硫属化合物）组成的垂直异质结构材料用于各种晶体管结构。这些晶体管大多数包含两个由薄隧穿势垒分隔的石墨烯导电层。这些晶体管属于垂直隧穿场效应晶体管（VTFET）类型。传统n型沟道MOSFET、p‐i‐n带间隧穿场效应晶体管（TFET）和 VTFET的示意图分别如图1a、1b和1c所示，以作区分。通用 VTFET的示意图示于图1c，该图重绘自参考文献7。高开关电流比、尖锐的共振隧穿特性以及适用于柔性透明电子器件是这种垂直石墨烯异质结构晶体管的一些已报道关键特性。然而，考虑到陡峭的亚阈值斜率和高驱动电流的要求，该晶体管在数字集成电路设计方面的潜力仍有不足。此外，部分已报道的VTFET在工作时还需要较高的电源电压（> 2 V）。对其中一些器件的研究是在低温环境下进行的，在室温下的性能较差。

在VTFET中，源极和漏极接触电极位于两个相对的导电层上，如图1c所示，这与图1a所示的传统四端MOSFET以及图1b所示的TFET中的接触电极不同。通过这种方式，源极和漏极之间的偏压（VDS）控制着由隧穿势垒分隔的两种导电材料之间载流子的垂直层间隧穿。然而，VDS掩盖了栅极电压对沟道静电势的实际控制作用。因此，在输出特性的不同栅极偏压下呈现出线性电阻行为，而非电流饱和。这阻碍了VTFETs在数字电路中的应用前景。此外，观察到的负微分电阻（NDR）也限制了 VTFETs的应用范围。因此，为了使石墨烯适用于数字集成电路设计，需要一种满足国际半导体技术路线图要求、具有高开关电流比、陡峭亚阈值斜率、非共振高漏极电流以及在亚0.5伏特操作下实现漏极电流饱和的石墨烯开关晶体管。

本工作提出了一种基于石墨烯‐氮化硼‐石墨烯垂直异质结构的石墨烯开关晶体管。GST的示意图如图1d所示，与图1c所示的通用VTFET有显著不同。然而，在源极和漏极的位置方面，GST与图1a所示的MOSFET具有相似性。与MOSFET、TFET和 VTFET相比，GST采用了不同的方法来调控沟道势垒高度。GST利用通过石墨烯‐氮化硼‐石墨烯异质结构的垂直隧穿机制来控制沟道势垒高度，从而最终调节源极和漏极之间的弹道输运。我们采用了文献26和27中讨论的基于“模式”的纳米尺度晶体管建模方法，用于GST的漏极电流估算，并据此绘制了GST的转移特性和输出特性。GST性能与国际半导体技术路线图（ITRS）预测的2020年 nMOSFET进行了比较。类似于CMOS反相器，设计了互补GST（p型GST和n型GST）反相器，并研究了其电压传输特性。

器件结构与工作原理

图1。（a）传统n沟道耗尽型MOSFET的示意图，（b）传统p‐i‐n带间隧穿场效应晶体管（TFET）的示意图，（c）参考文献7中提出的垂直隧穿场效应晶体管（VTFET）的示意图，以及（d）所提出的石墨烯开关晶体管（GST）的示意图。

在Si/SiO₂衬底上放置底部栅极接触，随后沉积多层氮化硼作为栅介质。接触电极的形成可采用热蒸发或溅射技术。第一性原理密度泛函理论（DFT）表明，通过在金属基底上吸附掺杂的石墨烯仍能保持其独特的电子特性。在石墨烯锥形点处观察到费米能级移动了 ∼0.5 eV。为简化起见，在我们的电流输运模型中，我们假设由于金属接触导致的石墨烯费米能级无移动。多层hBN可通过微机械剥离技术从氮化硼晶体获得。hBN埋层用作栅接触的底部栅介质，同时作为底层石墨烯层的衬底。氮化硼衬底相较于SiO₂衬底能够更好地保持石墨烯的电子特性，因此我们选择六方氮化硼作为顶栅和底栅的栅介质。此外，六方氮化硼与石墨烯之间的晶格失配仅为1.7%，使其适合作为层间隧穿势垒。我们假设源极和漏极采用掺杂接触电极。对于顶栅和底栅，通过金属‐氮化硼‐石墨烯异质结构形成金属‐绝缘体‐石墨烯隧穿结。由于六方氮化硼与石墨烯之间的晶格失配非常低，因而实现了较低的微分接触电阻。

石墨烯层的沉积可采用以下任意一种技术进行：微机械剥离、液相剥离或从经过化学气相沉积（CVD）生长石墨烯的金属基底上转移。位于埋入式hBN上方的石墨烯层被称为底层石墨烯层（GB）。源极和漏极接触电极放置在GB的两端，如图1d所示。随后在GB上方沉积原子级薄的多层hBN，接着沉积第二层石墨烯。该层被定义为顶层石墨烯层（GT）。最后，在GT上方进一步沉积多层hBN作为顶栅介质，然后进行金属接触沉积。顶部的金属接触称为顶栅电极。

对于GST，我们考虑了有效沟道面积为0.05 μm²，沟道长度为1 μm，宽度为50 nm。实验已观察到，电子可以在石墨烯中传播微米量级的距离而不发生散射，因此我们假设了一个理想的无散射石墨烯沟道，长度为1 μm。此外，这样的沟道长度简化了由短沟道效应带来的复杂性，降低了直接源‐漏隧穿效应的概率。在所考虑的GST沟道长度下，漏极电流受漏致势垒降低（DIBL）的影响也较小。

研究发现，量子限制石墨烯在纳米带形状（长度 ≫ 宽度）下，其带隙取决于边缘类型，呈现出可观测的带隙。对于扶手椅型石墨烯纳米带，随着纳米带宽度的减小，石墨烯纳米带的带隙增大。因此，50 nm宽度的石墨烯沟道可确保其为零带隙半导体。需要注意的是，当沟道宽度为1–10 nm时，将打开带隙，从而改变GST中的电流输运机制；而沟道宽度为> 50 nm时，对电流输运几乎没有额外影响。因此，我们假设50 nm的沟道宽度，在石墨烯与石墨烯纳米带之间提供了良好的近似。

继Britnell等人10的工作之后，GST考虑了上下hBN栅介质，每层厚度均为20 nm。三层hBN构成的层间隧穿势垒厚度为1.02 nm。Sciambi等人21研究发现，由纳米级隧穿势垒分隔的两层石墨烯不仅保持了隧穿相干长度，还保留了载流子的面外动量。当隧穿势垒厚度增加时，隧穿相干长度会显著下降。因此，我们将三层hBN的隧穿势垒厚度设为1.02 nm。需要注意的是，单层hBN的厚度为0.34 nm。然而，在此类垂直异质结构中，单层或双层hBN也可被采用，但它们更容易受到刻蚀的影响。

在图2a所示的关态下，GB和GT的费米能级保持平衡。我们假设在平衡状态下，费米能级与沟道狄拉克点重合，且由于粗糙度或缺陷不存在中间能态。栅极电压（VG）定义为底栅（VGB）与顶栅电压（VGT）之间的差值。为了开启晶体管，在GT和GB之间施加VG（VG = VGB ‐ VGT）。在位于GB的源极和漏极之间施加VDS。器件的关态定义为 |VG| = 0 V， |VDS| = 0.1 V；开态定义为 |VG| ≠ 0 V， |VDS| = 0.1 V。

为了实现低功耗，开关晶体管的电源电压需要符合国际半导体技术路线图（ITRS）要求之一。现有的基于硅和III‐V族材料的隧穿场效应晶体管（TFET）在亚0.5伏特电源电压下工作，因此要求开关晶体管在相等或更低的电源电压下运行。此外，研究发现基于石墨烯的晶体管可以在低压电源下工作，因此我们对GST在0.1 V电压下工作的假设与现有TFET性能和ITRS要求一致。

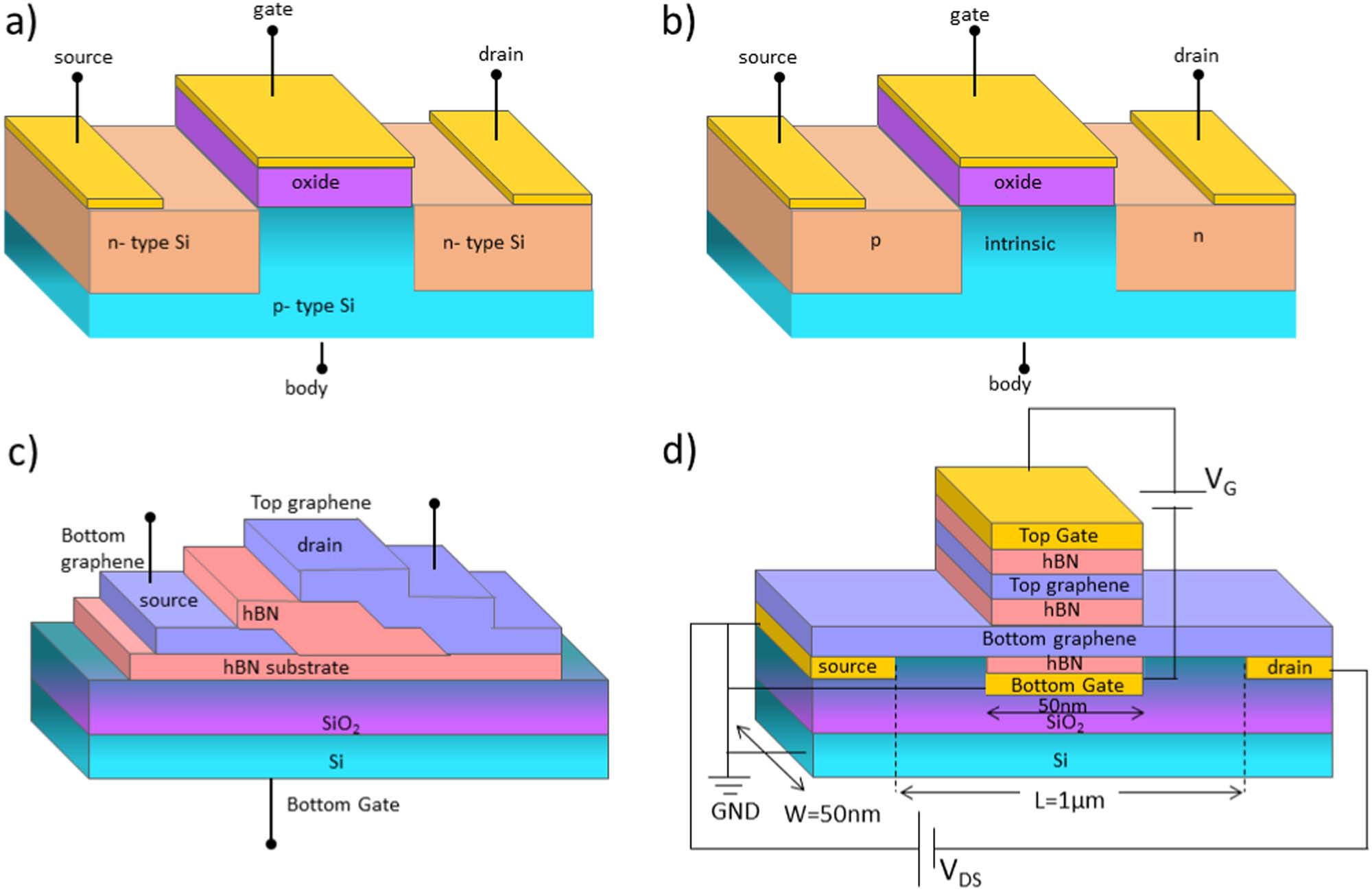
图2 (a) GST在关态下VG = 0 V和VDS = −0.1 V时的能带图，以及(b)开态下VG = 0.1 V和VDS = −0.1 V时的能带图。

EF_S、EF_C和EF_D分别为源极、沟道和漏极的费米能级。当施加VG时，上下石墨烯层之间发生层间载流子隧穿。由于隧穿产生的载流子浓度(N)使EF_C从沟道石墨烯层的狄拉克点移动了ΔEF，如图2b所示。这种费米能级移动导致EF_S和EF_D之间的势垒高度发生变化，从而通过VDS控制源极和漏极之间的电流输运。这样，漏极电流成为垂直隧穿的函数。需要注意的是，底层石墨烯层同时也是沟道石墨烯层。

根据参考文献11的实验研究发现，正栅极偏压使费米能级移至狄拉克点以上，而负栅极偏压使费米能级移至狄拉克点以下。因此，VG > 0提供ΔEF < 0，而VG < 0提供ΔEF > 0。

沟道势垒高度由两层石墨烯之间的垂直层间隧穿控制。需要注意的是，在VTFET中，层间隧穿偏压导致隧穿漏极电流，而在GST中，层间隧穿偏压改变沟道势垒高度，从而调控源漏弹道输运。传统的VTFET并未讨论任何源漏弹道输运机制。

当顶层和底层石墨烯层的狄拉克点未对齐时，层间隧穿载流子将穿过隧穿势垒。能量位于两个狄拉克点中间的电子对此电流有贡献。栅极电压引起的这种载流子隧穿变化也通过一个石墨烯层向另一个石墨烯层的波函数延展及其在底层石墨烯层中的相应重叠现象得到证实。对于正负栅极电压，均观察到波函数延展。这样，面外动量在较长的相干长度上得以保持，隧穿优选发生在纳米量级范围内。我们假设源极和漏极波函数不会与从顶层石墨烯层延伸到底层石墨烯层的波函数产生干涉。因此，垂直层间隧穿仅对沟道静电势的势垒控制有贡献。

电流输运模型

隧穿概率的估算

石墨烯费米能级移动所导致的有效势垒高度的变化主要取决于势垒的高度和形状。已经观察到，使用宽带隙单层二维半导体时，由于外部偏压引起的石墨烯费米能级变化接近或超过隧穿势垒的高度。然而，在宽带隙绝缘体的情况下，石墨烯费米能级的这种变化可以忽略不计。像hBN（带隙 > 5 eV）这样的宽带隙绝缘体在这方面起到了重要作用。

本节中，在确定隧穿概率时，考虑了特定的隧穿能量势垒高度（Φ）和厚度（d）。载流子从顶层石墨烯层隧穿到底层石墨烯层以及反向隧穿的隧穿概率。隧穿概率（TT）通过著名的WKB近似计算得出，

$$
TT(E) = \exp\left(-\frac{2d\sqrt{2m^*\Phi}}{\hbar}\right) \tag{1}
$$

在公式1中，d是隧穿势垒材料的厚度，Φ是空穴从石墨烯价带到hBN价带或电子从石墨烯导带到hBN导带的能量差，m*是隧穿势垒材料中电子的有效质量。

石墨烯狄拉克点与hBN价带顶之间的分离为1.5 eV，而相对于hBN导带的情况该值为> 4 eV。根据Britnell等人10的研究，我们选择Φ为1.5 eV。这得到空穴的隧穿有效质量m* = 0.5 m₀（m₀为自由电子质量），这也是hBN中空穴的有效质量。已经观察到，当两个石墨烯层之间存在一个势垒，且势垒一侧的费米面呈电子型而另一侧呈空穴型时，从一侧垂直入射的电子可以以100%效率在另一侧继续作为空穴传播。因此，对于空穴导电，将Φ选为1.5 eV是合理的并保持一致。对于相对论性载流子，可获得为1的完美隧穿概率。然而，对于非相对论性电子，则并非如此，其隧穿概率始终小于1。在谷间散射可忽略且晶格失配极低的情况下，垂直入射于势垒的电子不会产生反射。在GST中，我们还假设电子垂直入射于hBN势垒，其中石墨烯与hBN的晶格失配仅为1.7%。

电荷密度估算

当在上下石墨烯层之间施加偏压时，两个费米能级之间会呈现出相应的电势差。将上下石墨烯层之间的电势差视为Δφ，从顶层到底层石墨烯层的载流子隧穿过程描述如下：

$$
N_1 = \int_0^{\Delta\phi} D(E)TT(E)f_T(E)dE \tag{2}
$$

同样，从底层到顶层石墨烯层的载流子隧穿也可以表示如下，

$$
N_2 = \int_0^{\Delta\phi} D(E)TT(E)f_B(E)dE \tag{3}
$$

从顶层石墨烯层向底层石墨烯层的净载流子隧穿可以表示如下，

$$
N = N_1 - N_2 = \int_0^{\Delta\phi} D(E)TT(E)(f_T(E) - f_B(E))dE \tag{4}
$$

此处D(E)是石墨烯的态密度，f_T(E)是顶层石墨烯层的费米函数，f_B(E)是底层石墨烯层的费米函数，TT(E)是由公式1得到的隧穿概率。Δφ是积分限。在这种情况下，它是上下石墨烯层之间发生隧穿的总能量窗口。

石墨烯层中的态密度定义如下，

$$
D(E) = \frac{g_s g_v E}{2\pi(\hbar v_F)^2} \tag{6}
$$

其中E是隧穿发生的能量。对于所提出的GST电流输运模型，能量范围E被限制在0到Δφ之间。gₛ和gᵥ分别为自旋和谷简并度。对于石墨烯，gₛ = 2和gᵥ = 2。上下石墨烯层中的费米函数定义如下：

$$
f_T(E) = \frac{1}{1 + e^{(E - E_{Tf})/kT}} \tag{7}
$$

$$
f_B(E) = \frac{1}{1 + e^{(E - E_{Bf})/kT}} \tag{8}
$$

在公式7和8中，E_{Tf}和E_{Bf}分别为顶层石墨烯层和底层石墨烯层的费米能级位置。顶层石墨烯层的费米能级位于E_{Tf} = VG，底层石墨烯层的费米能级位于E_{Bf} = 0。结合公式5–8，公式5可改写如下：

$$
N = \int_0^{\Delta\phi} \frac{g_s g_v E}{2\pi(\hbar v_F)^2} TT(E)\left( \frac{1}{1 + e^{(E - E_{Tf})/kT}} - \frac{1}{1 + e^{(E - E_{Bf})/kT}} \right) dE \tag{9}
$$

将E_{Tf}和E_{Bf}的值代入后，式9可表示为如下形式，

$$
N = \int_0^{V_G} \frac{2E}{\pi(\hbar v_F)^2} TT(E)\left( \frac{1}{1 + e^{(E - V_G)/kT}} - \frac{1}{1 + e^{E/kT}} \right) dE \tag{10}
$$

从顶层到底层石墨烯层的隧穿能量窗口（Δφ）被假定为Δφ = E_{Tf} - E_{Bf} = VG - 0 = VG。现在将公式10从E = 0积分到E = Δφ = VG，费米‐狄拉克积分的闭式结果如下所示：

$$
N = \frac{g_s g_v}{2\pi(\hbar v_F)^2} TT(E)\left( \frac{V_G^2}{12} - V_G kT \ln[1 + \exp(V_G/kT)] - \frac{(\pi kT)^2}{12} - (kT)^2 \text{Poly log}(2, -\exp(V_G/kT)) \right) \tag{11}
$$

现在对于任意VG ≫ kT，发现前几项占主导地位，而后面的部分可以忽略，因此方程11可简化为：

$$
\frac{V_G^2}{2} - V_G kT \ln[1 + \exp(V_G/kT)] \gg \frac{(\pi kT)^2}{12} - (kT)^2 \text{Poly log}(2, -\exp(V_G/kT))
$$

因此，方程11的闭式解可表示如下，

$$
N = \frac{2}{\pi(\hbar v_F)^2} TT(E)\left( \frac{V_G^2}{12} - V_G kT \ln[1 + \exp(V_G/kT)] \right) \tag{12}
$$

方程12表示由于外加电压VG从顶层到底层石墨烯层隧穿的净载流子数量，如图3a所示。根据Georgiou等人11的研究，正偏压产生电子隧穿，而负偏压产生空穴隧穿。电子隧穿在图3a中用蓝色曲线表示，空穴隧穿用红色曲线表示，分别对应正偏压和负偏压。使用公式12计算得到的感应载流子浓度(N)与底层石墨烯层的费米能级具有平方根依赖关系，表达式如下：

$$
\Delta E_F = \pm \hbar v_F \sqrt{\pi |N|} \tag{13}
$$

费米能级移动的符号（正或负）由栅极电压的极性决定。正偏压使费米能级向上移动，如图2b所示。图3b显示了由于底层石墨烯层中感应载流子浓度(N)引起的费米能级移动量（ΔEF）的变化。图3b中的红线和蓝线表示基于VG极性的费米能级变化。

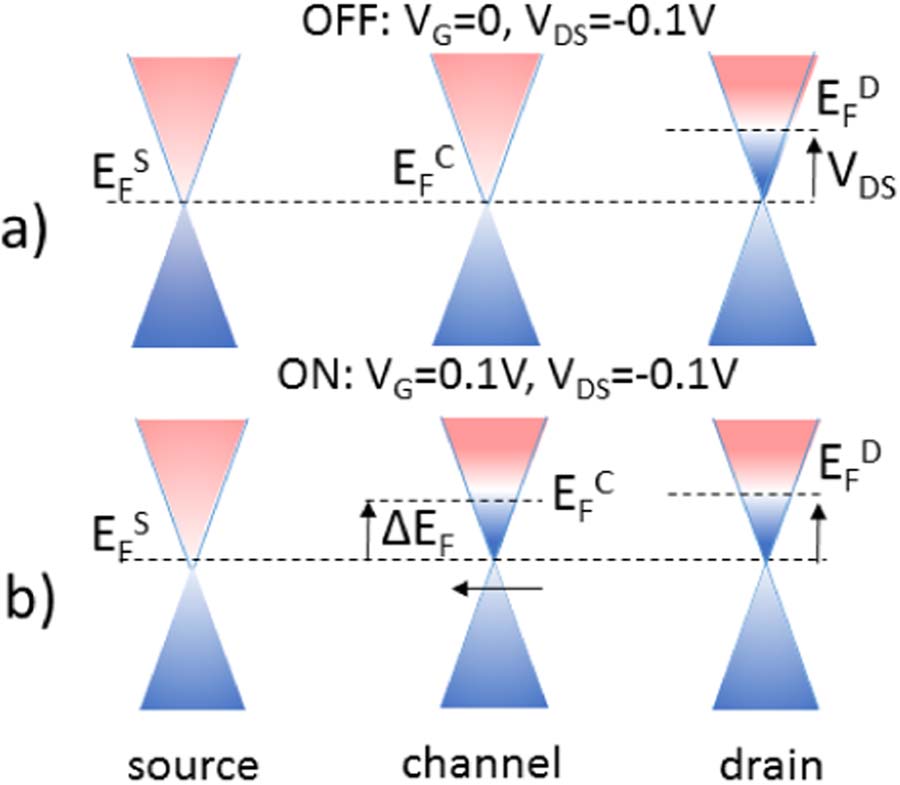
图3. (a) 载流子浓度(N)与VG的关系，(b) 费米能级(ΔEF)随载流子浓度(N)的变化，以及(c) GST操作的流程图

漏极电流的估算

基于纳米尺度晶体管的“模式”(M)建模方法，可以通过考虑沟道电导和传输系数来计算GST中的漏极电流。考虑到由于VG引起的垂直隧穿和由于VDS引起的横向输运的影响，GST中的漏极电流可使用朗道尔表达式表示如下，

$$
I = \int dE \left[ G(E)(f_S(E) - f_D(E)) \right] \tag{14}
$$

其中，G(E)为通道电导。f_S(E)和f_D(E)分别为源极和漏极的费米函数，其表达式与公式7和8类似。根据朗道尔表达式，电导(G(E))可表示如下，

$$
G(E) = \frac{2q^2}{\hbar} M(E) T(E) \tag{15}
$$

这里T(E)是透射系数，M(E)是石墨烯中的模式数量。石墨烯中模式数量(M)表示如下：

$$
M(E) = \frac{2W |E|}{\pi(\hbar v_F)} \tag{16}
$$

在公式16中，W是石墨烯通道宽度，|E|是计算横向模式的能量范围。本工作中，E被视为沟道中费米能级的偏移量（ΔEF），该偏移量控制源极和漏极之间沟道中的模式数量。在二维情况下，能量E处的导电通道数量与导体宽度成正比；在三维几何结构中，则与横截面积成正比。总模式数量还受到沟道材料能带结构的影响。公式16中M(E)的表达式是针对石墨烯的，不同于通常用于抛物线能带结构的模式表达式。v_F是费米速度。结合公式14–16，可将漏极电流表示如下：

$$
I = \frac{2q^2}{\hbar} \int dE \left[ M(E)T(E)(f_S(E) - f_D(E)) \right] \tag{17}
$$

假设沟道中存在无散射的源漏弹道输运，我们在公式17中将透射系数T(E)设为1。现在，结合弹道输运的能量窗口从0到VDS以及沟道势垒高度从0到ΔEF的变化，公式17可写为：

$$
I = \frac{2q^2}{\hbar} \left[ \int_0^{\Delta E_F} \frac{W 2|E|}{\pi(\hbar v_F)} \left( \frac{1}{1 + e^{(E - E_{FS})/kT}} - \frac{1}{1 + e^{(E - E_{FD})/kT}} \right) dE \right] \tag{18}
$$

方程的闭式解析解18如下所示，

$$
I = \frac{2q^2 V_T}{\hbar} \left[ \frac{W 2 \Delta E_F}{\pi(\hbar v_F)} \left( -\ln(1 + \exp(\Delta E_F/V_T)) + \ln(1 + \exp((\Delta E_F - V_{DS})/V_T)) + \ln 2 - \ln(1 + \exp(-V_{DS}/V_T)) \right) \right] \tag{19}
$$

在公式19中，kT被热电压qVT替代，其在300开尔文时的值定义为0.0259 eV。我们将此作为GST中的漏极电流方程，该方程适用于电子导电（n型行为）和空穴导电（p型行为），前提是考虑适当的偏压。图3c提供了GST操作的流程图及必要的电流输运方程。迁移率是GST中的一个重要参数。基于电导率的德鲁德模型（σ = μNq，其中σ为电导率，μ为载流子迁移率，q为电子电荷）以及石墨烯最小电导率（σ = 4q²/h，其中h为普朗克常数），我们计算得到GST的迁移率为5468 cm²/V·s。在0.1 V栅极偏压下，考虑诱导隧穿载流子浓度(N)为1.76 × 10¹¹/cm²用于迁移率提取。由于石墨烯能带结构在狄拉克点附近对称，因此电子和空穴迁移率的值几乎相同。

结果与讨论

使用公式19计算漏极电流，该电流同时依赖于TT和N。图4a中绘制的转移特性考虑了不同VDS下的固定隧穿概率（TT = 0.2378）。当VGS = 0.1 V且VDS = 0.1 V时，在有效沟道面积为0.05 μm²的情况下，获得的导通电流密度为88 μA/μm²。采用三层hBN（∼1.02 nm），在0.1 V电源电压下工作的GST以2.97毫伏每十倍频的亚阈值斜率开启，开关电流比为2.45 × 10⁴。关态漏电流为3.5 nA/μm²，对应的关态静态功耗为0.35 nW/μm²。在0.1 V电源电压下，对于驱动电流为88 μA/μm的情况，计算得到的GST动态功耗为4.4 μW/μm²。

将GST的转移特性与先前报道的一些VTFET在0.1 V栅极偏压下的表现进行比较，如图4b所示。图4b显示，先前报道的VTFET提供较低的导通电流密度和较高的亚阈值斜率。表I总结了从图4b获得的比较结果。针对数字电路的应用，我们避免了将类似的石墨烯‐绝缘体‐石墨烯器件（其表现出负微分电阻效应）列入表I和图4b中；因此仅与非NDR器件进行了比较。

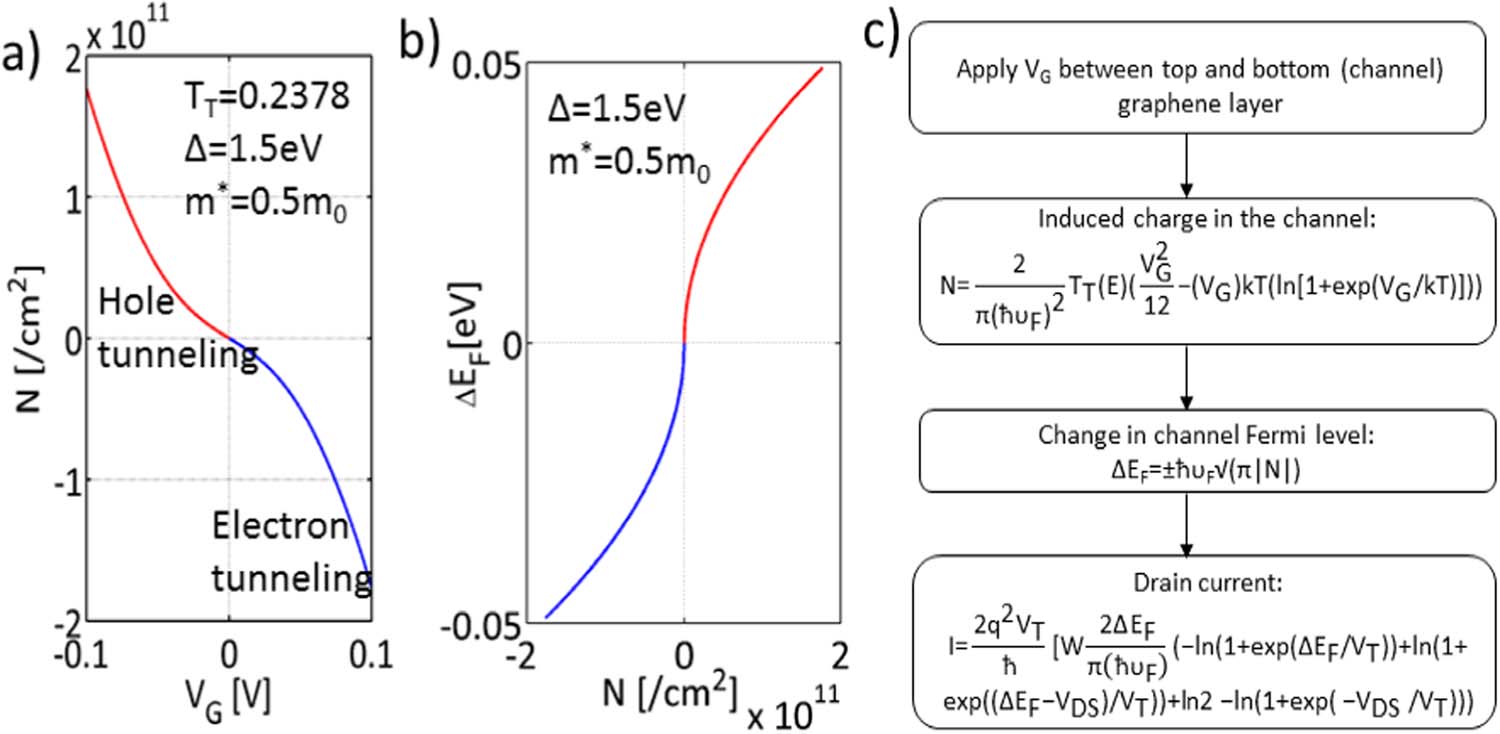
图4. GST的转移特性。（a）不同VDS下的ID‐VG曲线，线性尺度，步长为0.025 V；（b）GST与早期类似类型VTFETs的转移特性比较。

从图4b和表I中可以观察到，GST的性能优于其他类似的VTFET。在此阶段，需要进行几点说明以解释GST的高性能。我们采用了相当于厚度为1.02 nm的三层hBN作为隧穿势垒。而图4b和表I中列出的其他VTFET则考虑了更厚的隧穿势垒。如此低的势垒厚度不仅在底层石墨烯层中诱导出更高的电荷密度，而且在垂直方向上的能量动量仍保持守恒。这与相对较短的相干长度一致，有助于抑制负微分电阻效应。

国际半导体技术路线图（ITRS）要求下一代数字应用器件在VDD < 0.7 V下的开关电流比（ION/IOFF）最小值为10⁴。从表I可以看出，GST在VDD = 0.1 V时提供的ION/IOFF为2.45 × 10⁴，满足ITRS的要求。尽管与其他一些VTFET相比，GST的ION/IOFF较低，但仍适用于数字电路设计。需要指出的是，Georgiou等人11在石墨烯‐WS₂‐石墨烯VTFET中获得了在VDD = 2 V（>VDD的GST）范围内的电流比为10⁶，然而其亚阈值斜率大于GST在0.1 V供电电压下所获得的值。此外，WS₂是一种宽带隙半导体，而hBN是宽带隙绝缘体。石墨烯‐WS₂超晶格的电子特性不同于石墨烯‐hBN超晶格，因此GST的ION/IOFF与文献11中的ION/IOFF不同。

使用平均亚阈值斜率的方法，可以按如下方式确定SS。

$$
SS = \log_{10} \left[ \frac{I_D}{dI_D/dV_G} \right] \tag{20}
$$

其中ID为漏极电流，VG为栅极偏压。在亚阈值区漏极电流变化一个数量级时，所需的栅极偏压即为亚阈值斜率。图5显示了使用公式20提取亚阈值斜率的结果。需要指出的是，图5采用对数尺度绘制，而图4a采用线性尺度。表I中提到的SS值也通过图20和图4b计算得到。

对于能效高的开关技术，晶体管必须提供低于传统热离子极限60 mV/十倍频程的亚阈值斜率（SS）。由于大多数VTFET要么表现出负微分电阻（NDR）特性，要么表现为线性电阻特性，因此这类器件的亚阈值斜率（SS）并不总是被明确讨论。Roy等人提出的VTFET在TiOx/TiO₂堆叠结构中，当隧穿势垒为（x = 0.68–0.75）时，获得了70 mV/十倍频程的SS，且发现该值受限于栅极电容。他们报告指出，通过解耦栅极电容，SS可降至低至27 mV/十倍频程。

结合第一性原理密度泛函理论与非平衡格林函数（NEGF），Fiori等人15研究了石墨烯‐hBN‐石墨烯垂直异质结中极大的开态电流调制层。在漏源电压为0.5 V时，获得了相应的亚阈值摆幅∼300 mV/decade。这种性能的出现是由于栅极电压对沟道电势的静电控制能力较差。与垂直隧穿场效应晶体管相比，GST采用了一种混合机制，即载流子的垂直隧穿以及源极和漏极之间的横向弹道输运，其中栅极电容几乎没有影响。此外，费米能级移动控制源漏弹道输运，提供了更优的沟道静电控制能力。由于这些原因，与此前报道的VTFETs相比，GST实现了非常陡峭的亚阈值特性。

| 模型 | |VDD| 或 VDS∗∗ | |VG| | 隧穿势垒类型 | 开关电流比 | 亚阈值斜率（mV/十倍频） |
|—|—|—|—|—|—|—|
| 本工作 | 0.1 | 0.1 | hBN，3层 | 2.45 × 10⁴ | 2.97 |
| 参考文献10 | 25 | 0.1 | hBN，4层 | 10到10⁴ | 16 |
| 参考文献11 | 2 | 0.1 | WS₂, 4 layers | 10⁶ | 20 |
| 参考文献16 | 0.1 | 10 | hBN，5层 | 未指定 | 26 |
| 参考文献14 | 0.8 | 0 | TiOx/TiO₂, 5nm∗ | 未指定 | 70 |

∗x = 0.68–0.75。
∗∗文献中同时考虑了漏极偏压的两种表达形式。

表I. GST性能与类似V的比较 隧穿场效应晶体管

参数	2020 nMOSFET	GST	Unit
电源电压，VDD	0.68	0.1	V
驱动电流，ID	1942	880	μA/μm
关态漏电流，IOFF	100	3.5	nA/μm
关态漏功耗，∼ IOFFVDD	68	0.35	μW/μm
动态功耗，∼1/2 IDVDD	660.28	44	μW/μm

表II. 根据国际半导体技术路线图2012年版预测的GST与2020n‐MOSFET性能比较。

图5 从GST的ID-VG曲线提取亚阈值斜率。插图显示漏极电流变化一个数量级时VG的变化。插图中所示的值是使用公式20获得的。注：漏极电流以对数尺度绘制，与图4a中的线性尺度相对。

GST的转移特性高度依赖于隧穿势垒的厚度。因此，有必要研究不同隧穿势垒厚度下GST的性能。由于GST被设计为垂直异质结构，其隧穿势垒厚度由上下石墨烯层之间所用hBN层的数量决定。图6a展示了不同hBN层数下GST的转移特性。由公式1可知，隧穿概率随势垒厚度呈指数依赖关系。因此，当使用单层氮化硼（0.34 nm厚）作为隧穿势垒时，观察到导通电流密度为96.03 μA/μm²；当使用六层氮化硼时，该值下降至0.282 μA/μm²。导通电流与关态电流之比（ION/IOFF）也随hBN层数以及GST的亚阈值斜率而变化。图6b显示了不同hBN层数下的ION/IOFF和SS。随着隧穿势垒厚度随hBN层数增加，ION/IOFF减小。由于隧穿概率降低，GST的亚阈值斜率随hBN层数增加而增大。对于单层hBN，估计SS仅为0.9 mV/十倍频程，当hBN层数增至六层时，SS增加至20.31 mV/十倍频程。势垒厚度较小时，可实现对沟道的精确栅极控制。此外，顶层石墨烯层的波函数更容易向底层石墨烯层延伸。这不仅提供了高的导通电流密度，还降低了关态漏电流，并实现了陡峭的亚阈值斜率。因此，当hBN层数较少时，可观察到较高的ION/IOFF和较低的亚阈值斜率。

传统VTFET中的ID‐VDS特性存在显著的负微分电阻效应。因此，其在数字电路设计中的应用范围受到限制。然而，所提出的GST克服了此类限制，提供了无负微分电阻效应的输出特性，并具有独立的n型和p型行为。图7a和7b分别描绘了p型和n型GST在不同VG下的输出特性（ID-VDS）。与传统的MOSFET相比，当施加VDS > 0和VG < 0时获得n型电子输运，而当施加VDS < 0和VG > 0时获得p型空穴输运。由于正栅极偏压引起费米能级负向移动，负栅极偏压引起费米能级正向移动，图7中所用符号的正负与整体电流输运方向一致。图7假设p型和n型晶体管中的隧穿概率（TT）相等。

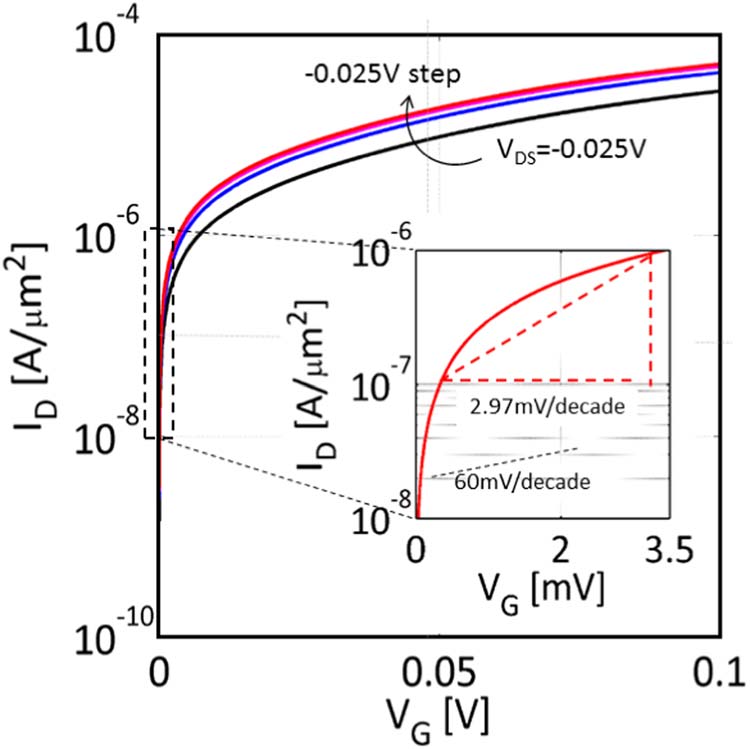
图6. (a) 以多层氮化硼层作为隧穿势垒时GST转移特性的变化，以及(b) 开关电流比（ION/IOFF）和亚阈值斜率（SS）随氮化硼层数的变化情况。

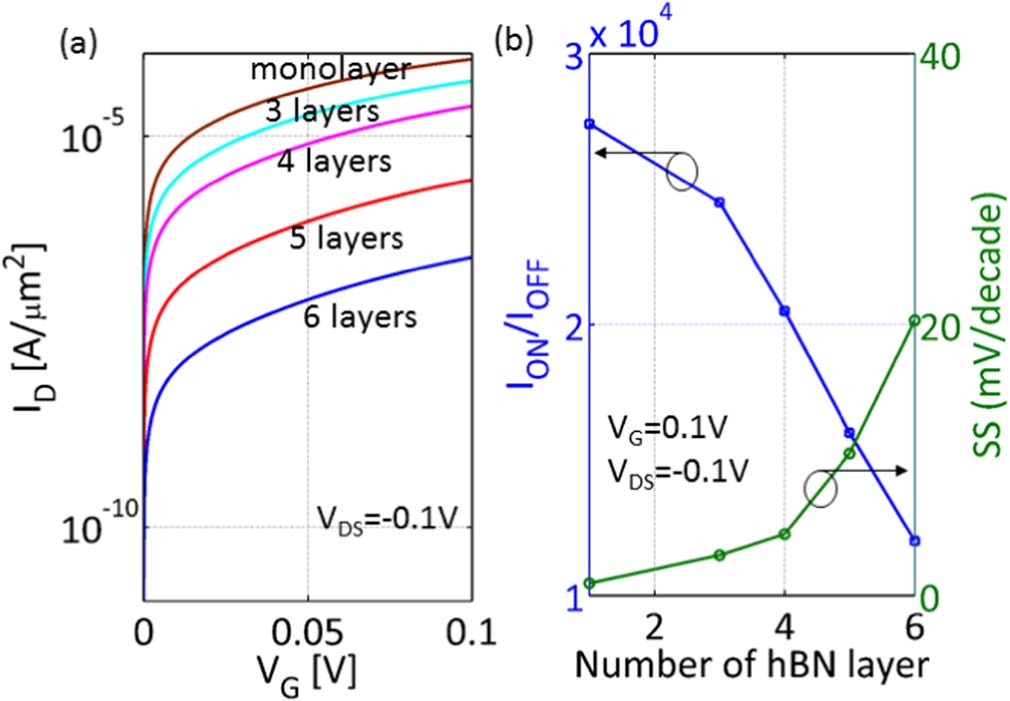
图7 GST的输出特性。a) 在VG > 0、VDS < 0下获得的p型行为；b) 在VG < 0、VDS > 0下获得的n型行为。

通过在顶层和底层石墨烯层上独立施加偏压，由于层间电子‐空穴相互作用，会产生强烈的库仑拖曳。当在栅极施加正偏压（VG > 0）时，顶层石墨烯层形成类电子费米面。进一步在漏极施加负偏压（VDS < 0）时，底层石墨烯层形成类空穴费米面。这两种相反类型的费米面对于实现以下两点至关重要：1）垂直于势垒的无散射弹性隧穿；2）有利于层间电子‐空穴相互作用的正库仑拖曳。类似地，当在顶层石墨烯层施加VG < 0、在底层石墨烯层施加VDS > 0时，可观察到具有无散射弹性隧穿的负库仑拖曳。因此，理解了获得输出特性时需要施加这种相反极性的偏压。图8a和8b分别显示了p型和n型GST在高VDS下的输出特性曲线。注意，在较高的VDS下，观察到漏极电流饱和现象。对于VDS < VG、VDS = VG和VDS > VG这三种情况，GST均表现出漏极电流饱和。这表明，在较高的漏极和栅极偏压下产生的库仑拖曳不仅实现了精确的层间隧穿，还保持了对沟道优异的栅极控制能力。因此，获得了平滑的输出特性。

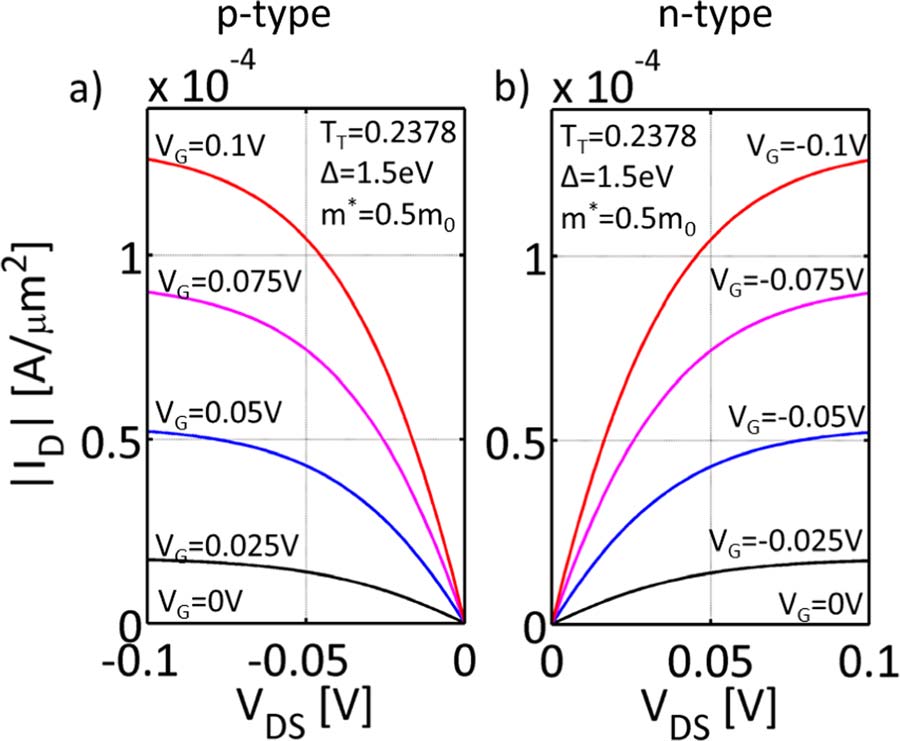
图8. 不同VG下随VDS增大的GST输出特性。(a) p型GST和(b) n型GST。

垂直反相器模型

反相器是数字集成电路的基本构建单元，其性能反映了用作开关的晶体管类型。使用垂直异质结构晶体管作为开关的互补反相器可以像CMOS反相器一样使用。图9a和9b分别展示了p型GST和n型GST的符号。由于GST在源漏弹道输运方面与弹道纳米级MOSFET具有相似性，因此我们的符号部分基于传统的耗尽型MOSFET符号设计。然而，由于沟道势垒控制是通过垂直层间隧穿实现的，我们采用了顶部和底部栅电极之间隧穿的传统符号。因此，图9a和9b中的符号结合了垂直层间隧穿和源漏弹道输运的概念。

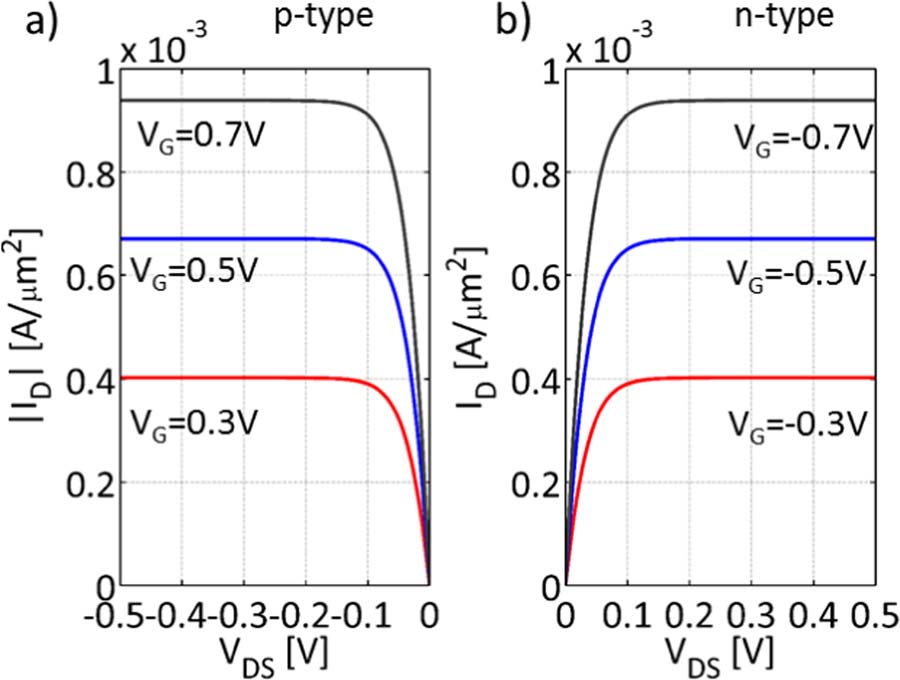
图9. (a) p型GST的符号 (b) n型GST以及(c)基于互补GST的垂直逻辑反相器示意图。

图9c展示了互补型GST垂直反相器的示意图。VGB,n、VGT,n、VGB,p和VGT,p分别为n型和p型晶体管的底栅电压和顶栅电压。栅极偏压（VG）定义为晶体管顶栅电压（VGT）与底栅电压（VGB）之间的差值。p型GST的底栅与n型GST的顶栅相连，因此称为共栅接触。在共栅接触处施加输入电压（VIN），将独立地在两个晶体管中引起费米能级相反类型的移动。n型GST的漏极连接到p型GST的源极，p型GST的漏极连接到电源电压（VDD），而n型GST的源极接地（0 V）。由于是垂直连接，GST垂直反相器仅需一个单个栅极接触。这样，无需额外互连来连接两个互补晶体管的栅极。

图10a显示了在不同电源电压下工作的互补GST反相器的电压传输特性(VTC)。当VDD = 0.5 V时，反相器增益(AV)为4.35，而当VDD = 0.1 V时，增益为3.15。这反映了GST反相器在降低的电源电压下仍具有较高增益的工作能力。与传统的CMOS反相器在电源电压低于0.5 V时增益急剧下降相比，GST垂直反相器在低压电源下仍能保持其增益。从转移特性中还可以注意到，在所有电源电压下均获得了从关到开状态的陡峭转换。图10b显示了GST反相器在VDD = 0.1 V时的噪声容限提取结果。我们计算得到低噪声容限NML为0.021 V，高噪声容限NMH为0.022 V。这两个值均超过原始信号的20%，证明了其具有较强的抗噪声能力。

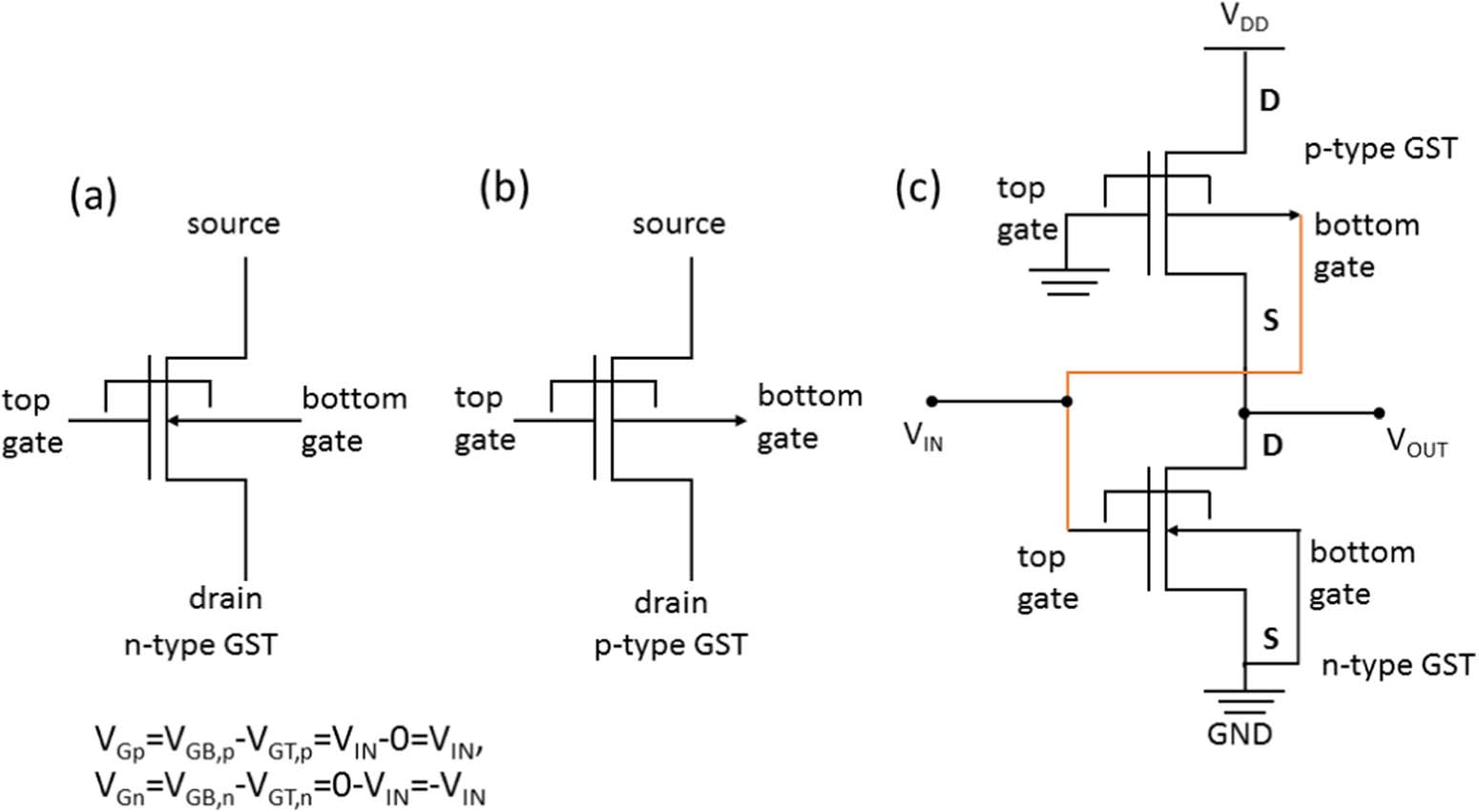
图10. (a) 不同电源电压下互补GST垂直反相器的电压传输特性及其对应的反相器增益，以及(b) 电源电压为0.1 V时的噪声容限。

总结

我们开发了一种基于石墨烯‐hBN‐石墨烯垂直异质结构的石墨烯开关晶体管的解析电流输运模型。在GST中，漏极电流在底层石墨烯层的源极和漏极之间流动。电流受沟道费米能级移动的调控，而费米能级的移动取决于载流子通过hBN从顶层石墨烯向底层石墨烯层的垂直隧穿。针对不同层数的hBN层，评估了GST的性能。除了将GST与类似的VTFET进行性能比较外，还提供了GST与ITRS预测的2020年nMOSFET的对比。在p型和n型操作下，GST的输出特性均表现出电流饱和，使其适用于数字电路设计。此外，GST还能够抑制负微分电阻效应，具有陡峭的亚阈值斜率和高开关电流比以及正常的室温下的操作。提出了一种类似于CMOS反相器的互补垂直反相器，并对其性能进行了分析。GST垂直反相器在低电源电压下具有大于1的反相器增益以及低噪声容限和高噪声容限。结论是，在0.1 V电源电压下，GST具有2.97毫伏每十倍频的亚阈值斜率和∼10⁴的电流比，满足国际半导体技术路线图对器件尺寸缩小在高能效电路设计方面的要求。