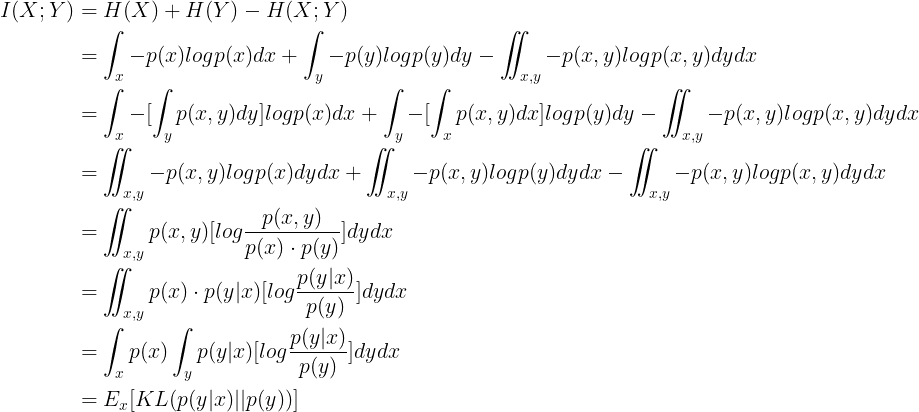
p(y)p(y)p(y)表示变量y的分布;
p(y∣x)p(y|x)p(y∣x)表示已知x的情况下y的分布;
KLKLKL表示两个分布之间的差异;
ExE_{x}Ex表示按变量x求期望。
由此可以看出,互信息其实就是:已知x之后y的分布 和 原始y分布 之间差异的期望。
把互信息写成KL散度的形式
最新推荐文章于 2025-09-23 14:36:27 发布
 本文介绍了互信息的概念,它是衡量已知变量x后变量y分布变化的一种度量方式。具体而言,互信息定义为已知x之后y的分布与原始y分布之间差异的期望。这一概念在信息论和概率论中具有重要意义。
本文介绍了互信息的概念,它是衡量已知变量x后变量y分布变化的一种度量方式。具体而言,互信息定义为已知x之后y的分布与原始y分布之间差异的期望。这一概念在信息论和概率论中具有重要意义。





















 5877
5877

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








