《动手学深度学习》学习笔记
数据操作

自动求导
变量设置求导
x = torch.ones(2, 2, requires_grad=True)
获得导数
out.backward()
这里要求因变量为标量,如果为tensor,则需要提供一个与因变量同大小的权重矩阵,通过加权求和所有元素来把输出的因变量变成标量,然后才能backward().
原因也很好理解:因变量之间是没有关系的,所有因变量元素只不过是放到一起,因此可以把他们排列当做一维向量做线性加权到一个标量l上。这样的好处是梯度就和因变量的纬度无关了,之间获得了l与自变量的梯度,不需要管因变量是个什么形状的tensor。
线性回归
梯度下降方法求解参数

上式是可以求解析解的。

也可以通过线性回归的方法通过梯度下降优化待求参数。通常使用小批量随机梯度下降(mini-batch stochastic gradient descent)方法,即小批量计算平均梯度,多批量优化参数。

这里还乘以了一个学习率,相当于梯度下降方法中的step大小,刚开始可以大一点,后面要小一点。
全连接层(稠密层)
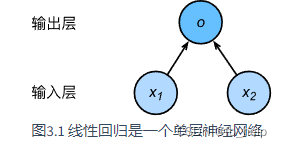

线性回归
- 构建模拟数据,确定输入(features),输入(label),参数
- 写data loader(把数据拆分成batch)
- 构建 function (net) , loss 和优化方法
- 迭代epoch求解

线性回归简洁版
-
数据读取

-
定义自己的function,需要给定参数个数和forward函数。其实是输入与输出之间的函数关系。因此,要给出输入和输出的计算方法,即forward函数。神经网络把这种函数关系用网格结构来代替。

-
用torch的net结构

-
损失
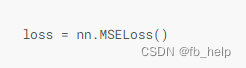
-
优化方法






 这篇博客介绍了深度学习的基础,包括数据操作、自动求导的概念,详细阐述了如何使用PyTorch进行变量设置及求导。线性回归的解析解和梯度下降方法被用来优化参数,特别是小批量随机梯度下降在训练过程中的应用。此外,还讲解了全连接层在实现线性回归时的步骤,包括构建模拟数据、定义网络结构、损失函数和优化方法。
这篇博客介绍了深度学习的基础,包括数据操作、自动求导的概念,详细阐述了如何使用PyTorch进行变量设置及求导。线性回归的解析解和梯度下降方法被用来优化参数,特别是小批量随机梯度下降在训练过程中的应用。此外,还讲解了全连接层在实现线性回归时的步骤,包括构建模拟数据、定义网络结构、损失函数和优化方法。

















 1531
1531

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








