【算法简述】图论专题：欧拉回路

最新推荐文章于 2025-05-15 09:37:32 发布

Cancelleds

最新推荐文章于 2025-05-15 09:37:32 发布

阅读量459

点赞数

CC 4.0 BY-SA版权

分类专栏：算法图论数学系列

本文链接：https://blog.youkuaiyun.com/ebirth/article/details/91354290

本文探讨了欧拉回路在图论中的应用，强调了解决一笔画问题的关键在于图的性质。针对有向图和无向图，分别提出了要求每个节点的入度等于出度或节点度数为偶数的条件。通过题目样例和实际代码展示，解释了欧拉回路的算法思路，并提供了相关题目链接以供进一步实践。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

图论问题概述总结

- 欧拉回路
- 题目样例

对于图论，我们尊熟悉的算法是比较多的，这次，我就找了集中常用的算法。

欧拉回路

欧拉回路就是在一张有向或无向图中求出一笔画问题的具体画法。
方法：

先思考此题是否是用欧拉回路来解决。
思考是有向图或无向图来解决适用于欧拉回路。
对于有向图，保证每个点的入度为出度；对于系数图，保证每个点为偶数。

我们对于这个算法，可以用来图：

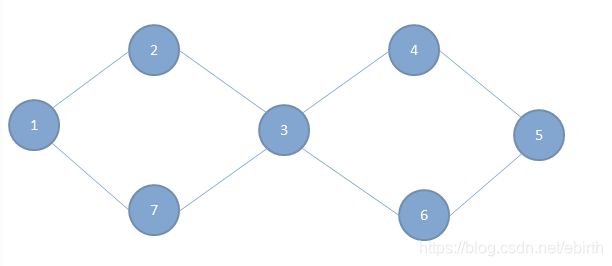
题目样例

就向这样，接下来，我们看看代码：
题：http://120.77.248.79/problem/3023105

#include<bits/stdc++.h>
using namespace std;
const int maxn=200000;
const int maxm=200000;
struct node{
	int v,next;
	int len;
}e[maxm];
int g[maxn],ans;
void init(){
	memset(g,-1,sizeof(g));
	ans=0;
}
void add(int u,int v){
	e[ans].v=v;
	e[ans].next=g[u];
	g[u]=ans++;
}
int n,m;
int degree[maxn];
int cnt;
bool vis[maxn];
void dfs(int u){
	vis[u]=true;
	cnt++;
	for (int i=g[u];i!=-1;i=e[i].next){
		int v=e[i].v;
		if (!vi