题解-倒水问题

题目样解

题目背景
输入输出已更改，请不要直接提交原先的代码。
题目描述
假定两个水壶A和B，供水量不限。可以使用三种方法装水：

给一个水壶装水；
把一个水壶倒空；
从一个水壶倒进另一个水壶。
当从一个水壶倒进另一个水壶时，如果第一个水壶倒空，或者第二个水壶装满就不能再倒了。例如，一个水壶A是5加仑和另一个水壶B是6加仑，水量是8加仑，则从水壶A倒进水壶B时，让水壶B充满水而水壶A剩3加仑水。
问题由3个参数：C_a，C_b 和N，分别表示水壶A和B的容量，目标水量N。解决问题的目标是，给出一系列倒水的步骤，使水壶B中的水量恰好是N。

输入输出格式
输入格式：
第一行为数据组数T。

接下来的TT行，每行三个数字C_aC，C_b和N，意义如题目所示。T不超过30300<C_a≤Cb,N≤C_b≤1000C_a和C_b互质。

输出格式：
输出共为T行，第一个数字为要达成的完成次数a_i （题目保证存在解）。

接下来a_i个数字，表示各种操作：

1操作:fill A意为给A灌满水
2操作:fill B
3操作:empty A意为将A中水倒空
4操作:empty B
5操作:pour B A意为将B中水倒到A中（直到A满或者B中水没有剩余）
6操作:pour A B
输入输出样例
输入样例#1：
2
3 5 4
5 7 3
输出样例#1：
6 2 5 3 5 2 5
6 1 6 1 6 4 6
输入样例#2：
1
26 29 11
输出样例#2：
22 1 6 1 6 4 6 1 6 4 6 1 6 4 6 1 6 4 6 1 6 4 6
说明
开启了spj。
如果你的方案比答案优，会提示UKE，此时请联系管理员修改数据。
如果你的方案比答案差，分数会相应减损。

解题思路

做这个题，首先想到的应是深搜，宽搜，但是本人认为用宽搜更直白一些。
当然，两种方法都行。首先，是两个水壶a和b。用一个二维数组来记录水壶a,b的情况，（注：数据范围大，最好开一个比较大的数组）。

解题过程

按照题目中所给的信息，我们必须按照六个步奏依次进行，如图：

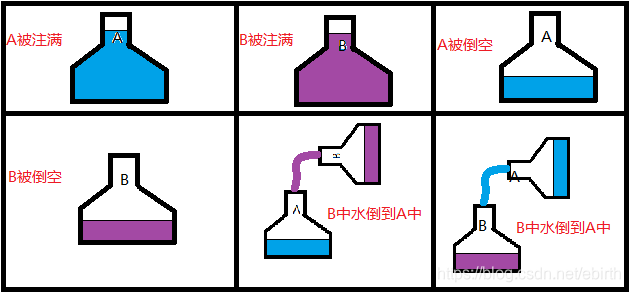
代码实现

如图可知，代码的基本结构为：

if(!vis[ca][b]){
			qu.push(node(ca,b,s+"1"));
			vis[ca][b]=1;
		}
		if(!vis[a][cb]){
			qu.push(node(a,cb,s+"2"));
			vis[a][cb]=1;
		}
		if(!vis[0][b]){
			qu.push(node(0,b,s+"3"));
			vis[0][b]=1;
		}
		if(!vis[a][0]){
			qu.push(node(a,0,s+"4"));
			vis[a][0]=1;
		}
		int c=a+b>ca?ca:a+b;
		if(!vis[c][a+b-c]){
			qu.push(node(c,a+b-c,s+"5"));
			vis[c][a+b-c]=1;
		}
		c=a+b>cb?cb:a+b;
		if(!vis[a+b-c][c]){
			qu.push(node(a+b-c,c,s+"6"));
			vis[a+b-c][c]=1;
		}

当然，这样写可以把六种情况一一列举，（其他的那个变量就自己去想了(～￣▽￣)～ ），按照描述，我们根据他便可以将BFS不断扩展下去，最后等水量为N的时候，就完了。
可能你会嫌代码量大，（￣へ￣），但你可以参照下面的方式：

int fd=a+b>ca?ca:a+b;//B->A
int fg=a+b>cb?cb:a+b;//A->B
const int dir[6][3]={
	{ca,b,1},
	{a,cb,2},
	{0,b,3},
	{a,0,4},
	{fd,a+b-fd,5},
	{a+b-fg,fg,5},
};
for(int i=0;i<6;i++){
	if(!vis[x[i][0]][x[i][1]]){
		qu.push(node(x[i][0],x[i][1],s+char('0'+x[i][2])));
		vis[x[i][0]][x[i][1]]=1;
	}
}

好了（(￣.￣)），我就不多说了，至于DFS的，可以自己去上网查查，也可以去洛谷，最后——

AC代码

#include <bits/stdc++.h>
using namespace std;
int ca,cb,n;
bool vis[4000][4000];
struct node{
	int a,b;
	string s;
	node(){}
	node(int qa,int qb,string ss){
		a=qa;
		b=qb;
		s=ss;
	}
};
queue<node> qu;
void bfs(){
	qu.push(node(0,0,string()));
	vis[0][0]=1;
	while(!qu.empty()){
		int a=qu.front().a;
		int b=qu.front().b;
		string s=qu.front().s;
		qu.pop();
		if(b==n){
			cout<<s.size();
			for(int i=0;i<s.size();i++){
				cout<<" "<<s[i];
			}
			cout<<endl;
			return;
		}
		if(!vis[ca][b]){
			qu.push(node(ca,b,s+"1"));
			vis[ca][b]=1;
		}
		if(!vis[a][cb]){
			qu.push(node(a,cb,s+"2"));
			vis[a][cb]=1;
		}
		if(!vis[0][b]){
			qu.push(node(0,b,s+"3"));
			vis[0][b]=1;
		}
		if(!vis[a][0]){
			qu.push(node(a,0,s+"4"));
			vis[a][0]=1;
		}
		int c=a+b>ca?ca:a+b;
		if(!vis[c][a+b-c]){
			qu.push(node(c,a+b-c,s+"5"));
			vis[c][a+b-c]=1;
		}
		c=a+b>cb?cb:a+b;
		if(!vis[a+b-c][c]){
			qu.push(node(a+b-c,c,s+"6"));
			vis[a+b-c][c]=1;
		}
	}
	return;
}
int main() {
    int t;
    cin>>t;
    while(t--){
    	memset(vis,0,sizeof(vis));
    	while(!qu.empty())qu.pop();
    	cin>>ca>>cb>>n;
    	bfs();
	}
    return 0;
}

抄袭者，死无对证。