题解-连接格点

连接格点

描述

有一个M行N列的点阵，相邻两点可以相连。一条纵向的连线花费一个单位，一条横向的连线花费两个单位。某些点之间已经有连线了，试问至少还需要花费多少个单位才能使所有的点全部连通。

输入

第一行输入两个正整数m和n, 其中 1 <= n,m <= 1000。

以下若干行每行四个正整数x1,y1,x2,y2，表示第x1行第y1列的点和第x2行第y2列的点已经有连线。输入保证|x1-x2|+|y1-y2|=1。

输出

输出使得连通所有点还需要的最小花费。

输入样例 1

2 2
1 1 2 1

输出样例 1

3

此题使用并查集，最好用图表的形式来写。
重要信息：

• 某些点之间已经有连线了，试问至少还需要花费多少个单位才能使所有的点全部连通
• 以下若干行每行四个正整数x1,y1,x2,y2，表示第x1行第y1列的点和第x2行第y2列的点已经有连线。输入保证|x1-x2|+|y1-y2|=1。
• 输出使得连通所有点还需要的最小花费。

因为这道题格点为重要信息，因此，你最先想到的肯定是二维数组。
二维数组图表：

这就只能用（x,y）的坐标来表示了，所以要用pair来写。但是，你是否想过，这会处理很长的一片。
因此，我们用一维数组更好一些。
但是，我们要怎么表示呢？——标记
如图：

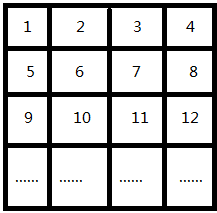
很简单，我们将行和列的数字一 一标记，这样，我们就方便了很多。
一个问题，因为标记了，就是去了二维数组查找的功能，怎么办？

x*m+y

这是一个算术，我们用这个来表示位置。（但这是从2开始找的，习惯从1开始找，就改变成x*m+y-m）最好用函数来表示。
实现此结构：

int convert(int x,int y){
	return x*m+y-m;
}

中间使用函数初始化：

void init(){
	for(int i=1;i<=m;i++){
		for(int j=1;j<=n;j++){
			fa[convert(i,j)]=convert(i,j);
		}
	}
}

然后，我们就要处理并查集的结构了：

int get(int x){
	if(fa[x]==x){
		return x;
	}
	fa[x]=get(fa[x]);
	return fa[x];
}
void merge(int x,int y){
	fa[get(x)]=get(y);
}

接下来，在main函数里写下：

while(cin>>a>>b>>c>>d){
		merge(convert(a,b),convert(c,d));
}

merge用来合并两个点，就变成了线。
接下来处理行（m为行，n为列）：

for(int j=1;j<=n;j++){
		for(int i=1;i+1<=m;i++){
			if(get(convert(i,j))!=get(convert(i+1,j))){
				merge(get(convert(i,j)),get(convert(i+1,j)));
				ans++;
			}
		}
	}

这样，使行后面就合并了，如果他们不相等，就无法连接，于是就然他们是连接的。统计行的个数。
接下来统计列：

for(int i=1;i<=m;i++){
		for(int j=1;j+1<=n;j++){
			if(get(convert(i,j))!=get(convert(i,j+1))){
				merge(get(convert(i,j)),get(convert(i,j+1)));
				ans+=2;
			}
		}
	}

与行类似，但这里每次加两次，因为列上在数组里有2n次。
注意，范围大，数组要超过1000000。
实现代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn=10000010;
int m,n;
long long a,b,c,d;
long long fa[maxn];
int convert(int x,int y){
	return x*m+y-m;
}
void init(){
	for(int i=1;i<=m;i++){
		for(int j=1;j<=n;j++){
			fa[convert(i,j)]=convert(i,j);
		}
	}
}
int get(int x){
	if(fa[x]==x){
		return x;
	}
	fa[x]=get(fa[x]);
	return fa[x];
}
void merge(int x,int y){
	fa[get(x)]=get(y);
}
int main(){
	cin>>m>>n;
	init();
	long long ans=0;
	while(cin>>a>>b>>c>>d){
		merge(convert(a,b),convert(c,d));
	}
	for(int j=1;j<=n;j++){
		for(int i=1;i+1<=m;i++){
			if(get(convert(i,j))!=get(convert(i+1,j))){
				merge(get(convert(i,j)),get(convert(i+1,j)));
				ans++;
			}
		}
	}
	for(int i=1;i<=m;i++){
		for(int j=1;j+1<=n;j++){
			if(get(convert(i,j))!=get(convert(i,j+1))){
				merge(get(convert(i,j)),get(convert(i,j+1)));
				ans+=2;
			}
		}
	}
	cout<<ans;
	return 0;
}

作者:rebirth.death