poj 1848 树形dp（添加最少的边每点都恰在一个圈中）

题意：给定一棵无根树，问至少需要添加多少条边，使得每个节点属于且仅属于一个圈，并且，每个圈的节点数至少为3（即不算环和重边）。若无解则输出-1，否则输出至少添加的边数。

思路：不会做，看的别人的解体报告。

思路当然是树形dp。每个点设置三个状态：

1、f[0, x]表示以x为根的子树，变成每个顶点恰好在一个圈中的图，需要添加的最少边数。

2、f[1, x]表示以x为根的子树，除了根x以外，其余节点变成每个节点恰好在一个圈中的图，需要添加的最少边数。

3、f[2, x]表示以x为根的子树，除了根x以及其所在的一条链（*链长度要大于1）以外，其余节点变成每个节点恰好在一个圈中的图，需要添加的最少边数。

于是状态转移方程（解释见下面四张图便清楚了，假设当前结点x共有k个儿子节点）：
i,j,v∈thesetofx′sson,i≠j
f[0, x] = min{
sum{f[0, v]} – max{f[0, i] – f[2, i]} ,
sum{f[0, v]} – max{f[0, i] – min{f[1, i], f[2, i]} – max{f[0, j] – min{f[1, j], f[2, j]}}
}
f[1, x] = sum{f[0, v]}
f[2, x] = sum{f[0, v]} – max{f[0, i] – min{f[2, i], f[1, i]}}

A.根R的所有子树自己解决（取状态0），转移到R的状态1。即R所有的儿子都变成每个顶点恰好在一个环中的图，R自己不变。

B.根R的k-1个棵树自己解决，剩下一棵子树取状态1和状态2的最小值，转移到R的状态2。剩下的那棵子树和根R就构成了长度至少为2的一条链。

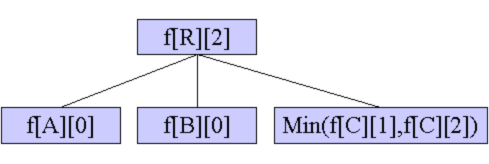
C.根R的k-2棵子树自己解决，剩下两棵子树取状态1和状态2的最小值，在这两棵子树之间连一条边，转移到R的状态0。

D.根R的k-1棵子树自己解决，剩下一棵子树取状态2（子树里还剩下长度至少为2的一条链），在这棵子树和根之间连一条边，构成一个环，转移到R的状态0。

#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <algorithm>
#include <queue>
using namespace std;
#define INF 1001
#define clr(s,t) memset(s,t,sizeof(s))
#define N 105
int n;
int dp[N][3],first[N],top;
struct edge{
    int y,next;
}e[N<<1];
void add(int x,int y){
    e[top].y = y;
    e[top].next = first[x];
    first[x] = top++;
}
void dfs(int x,int fa){
    int i,y,a,sum,num,tmp;
    num = sum = 0;
    tmp = -INF;
    for(i = first[x];i!=-1;i=e[i].next){
        y = e[i].y;
        if(y != fa){
            dfs(y, x);
            sum += dp[y][0];
            num ++;//num是儿子的数量
            if(tmp < dp[y][0] - min(dp[y][1],dp[y][2])){//求出最小值存入tmp，存储边的索引，即变量a是为了后面求次小值
                tmp = dp[y][0] - min(dp[y][1],dp[y][2]);
                a = i;
            }
        }
    }
    dp[x][1] = sum;//对应图A
    if(!num)
        return;
    dp[x][2] = sum - tmp;//对应图B
    for(i = first[x];i!=-1;i=e[i].next){
        y = e[i].y;
        if(y!=fa){
            dp[x][0] = min(dp[x][0] , sum-dp[y][0]+dp[y][2]+1);//对应图D
            if(i!=a)
                dp[x][0] = min(dp[x][0] , sum-tmp-dp[y][0]+min(dp[y][1],dp[y][2])+1);//对应图C
        }
    }
}
int main(){
    int i,a,b;
    scanf("%d",&n);
    clr(first, -1);
    top = 0;
    for(i = 1;i<n;i++){
        scanf("%d %d",&a,&b);
        add(a,b);
        add(b,a);
    }
    for(i = 1;i<=n;i++)
        dp[i][0] = dp[i][1] = dp[i][2] = INF;
    dfs(1,0);
    if(dp[1][0] >= INF)
        printf("-1\n");
    else
        printf("%d\n",dp[1][0]);
    return 0;
}