本文通过一维的高斯数值积分,进行第一型曲线积分的数值实现。一维的高斯数值积分实现已在博主之前的文章当中给出,本文不再叙述,并且可以通过Gauss_int_1D函数来直接调用。
对于第一型曲线积分,即
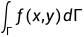
其中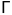 为从
为从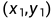 )到
)到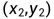 的光滑线段,有函数表达式
的光滑线段,有函数表达式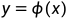 .
.
那么,通过高等数学中的知识,我们可以得到
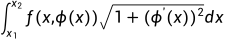
此时,原曲线积分变成了一维上的定积分,这样我们就可以通过映射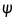 :
: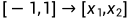 ,即
,即
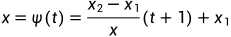
将原区间投影到[-1,1]的高斯数值积分标准区间上面.此时可以得到积分为
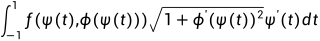
那么下面我将叙述数值实现,代码均通过Matlab完成
function [r] = Cal_Line_int(a,b,f,phi)
%a为曲线的左端点,即(x1,y1)
%b为曲线的右端点,即(x2,y2)
%f为被积函数
%phi为a与b的线段函数表达式
x_1 = a(1);
y_1 = a(2);
x_2 = b(1);
y_2 = b(2);
f_1 = subs(f,y,phi);
psi = (x_2-x_1)*(t+1)/2+x_1;
f_2 = subs(f_1,x,psi);
phi_1 = subs(phi,x,psi);
gauss_f = f_2*sqrt(1+(diff(phi_1))^2)*(x_2-x_1)/2;
r = guass_int_1D(gauss_f);
end注:其中
f_1为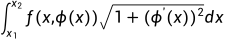 中的
中的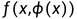 ,
,
f_2为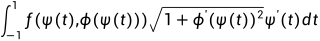 中的
中的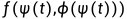 ,
,
gauss_f为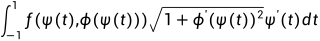 中的
中的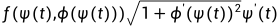 .
.




















 959
959

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








