cost function:
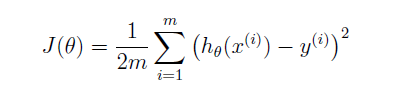 , where
, where 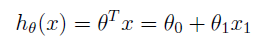
我们的目的是找到最优的两个参数theta 0, theta 1, 来使得cost function 值最小。
方法:Gradient Descent(又叫Batch Gradient Descent)
问题描述:Suppose you are the CEO of a restaurant franchise and are considering different cities for opening a new outlet. The chain already has trucks in various cities and you have data for profits and populations from the cities. You would like to use this data to help you select which city to expand to next. The file ex1data1.txt contains the dataset for our linear regression problem. The first column is the population of a city and the second column is the profit of a food truck in that city. A negative value for profit indicates a loss.
MATLAB代码实现:
clear ; close all; clc
data = load('ex1data1.txt');
X = data(:, 1); y = data(:, 2);
m = length(y); % number of training examples
% Plot Data
plot(X, y, 'rx', 'MarkerSize', 10); % Plot the data
ylabel('Profit in $10,000s'); % Set the y axis label
xlabel('Population of City in 10,000s'); % Set the x axis label
%% =================== Part 1: Cost and Gradient descent ===================
X = [ones(m, 1), data(:,1)]; % Add a column of ones to x
theta = zeros(2, 1); % initialize fitting parameters
% Some gradient descent settings
iterations = 1500;
alpha = 0.01;
for i=1:iterations
theta_s=theta;
theta(1) = theta(1) - alpha / m * sum(X * theta_s - y);
theta(2) = theta(2) - alpha / m * sum((X * theta_s - y) .* X(:,2));
end
% Plot the linear fit
hold on; % keep previous plot visible
plot(X(:,2), X*theta, '-')
legend('Training data', 'Linear regression')
hold off % don't overlay any more plots on this figure
% Predict values for population sizes of 35,000 and 70,000
predict1 = [1, 3.5] *theta;
predict2 = [1, 7] * theta;
%% ============= Part 2: Visualizing J(theta_0, theta_1) =============
% Grid over which we will calculate J
theta0_vals = linspace(-10, 10, 100);
theta1_vals = linspace(-1, 4, 100);
% initialize J_vals to a matrix of 0's
J_vals = zeros(length(theta0_vals), length(theta1_vals));
% Fill out J_vals
for i = 1:length(theta0_vals)
for j = 1:length(theta1_vals)
t = [theta0_vals(i); theta1_vals(j)];
J_vals(i,j) = computeCost(X, y, t);
end
end
% Because of the way meshgrids work in the surf command, we need to
% transpose J_vals before calling surf, or else the axes will be flipped
J_vals = J_vals';
% Surface plot
figure;
surf(theta0_vals, theta1_vals, J_vals)
xlabel('\theta_0'); ylabel('\theta_1');
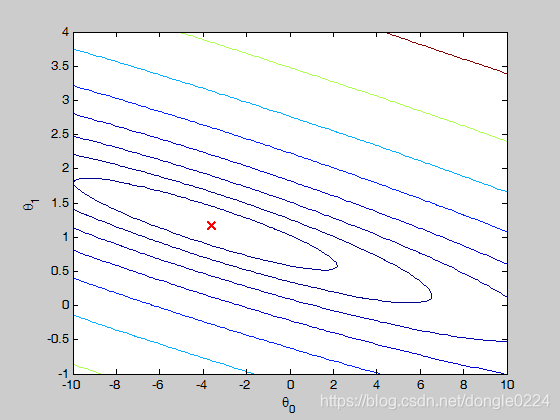
% Contour plot
figure;
% Plot J_vals as 15 contours spaced logarithmically between 0.01 and 100
contour(theta0_vals, theta1_vals, J_vals, logspace(-2, 3, 20))
xlabel('\theta_0'); ylabel('\theta_1');
hold on;
plot(theta(1), theta(2), 'rx', 'MarkerSize', 10, 'LineWidth', 2);
运行结果:predict1=0.4520;predict2=4.5342
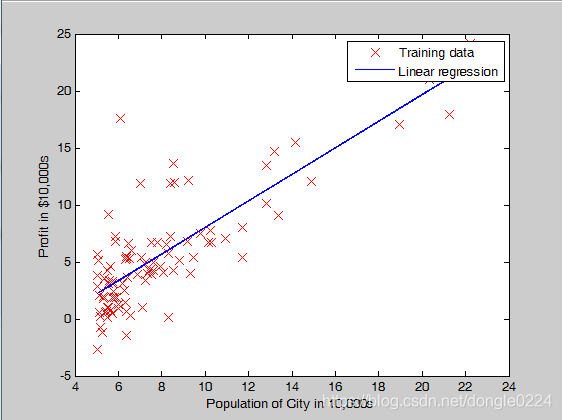
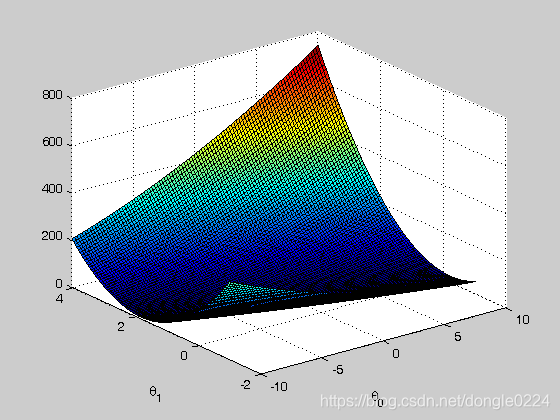







 本文通过一个餐厅连锁店的案例,详细介绍了如何使用线性回归和梯度下降算法预测城市利润。利用MATLAB代码实现了算法过程,展示了数据可视化和成本函数优化,最终预测了不同城市规模的预期利润。
本文通过一个餐厅连锁店的案例,详细介绍了如何使用线性回归和梯度下降算法预测城市利润。利用MATLAB代码实现了算法过程,展示了数据可视化和成本函数优化,最终预测了不同城市规模的预期利润。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








