A*算法与PRM在室内火灾模拟中的算法对比
1. 引言
根据Moncada等人[9]的研究,仅在美国,每79秒就会发生一起住宅火灾,此外,80%的死亡发生在家中。为了扑灭火灾,救援队伍必须接受充分的培训,并掌握足够的现场信息,以便制定扑灭火灾或营救可能受害者的策略。这些信息包括了解火灾可能蔓延的路线和人员逃生路线。一旦确定了火灾起始位置和蔓延模式,就可以开始灭火。世界上一些消防部门,特别是在第一世界国家,会使用受控火灾设施来训练其人员并验证这些模式。这种做法具有风险,且会产生直接和间接成本,许多消防部门难以承担。
这些成本可以直接反映,例如使用易燃材料的成本,也可以通过测量为此活动设置场景所需的时间间接体现。需要注意的是,如果火灾失控,试图扑灭火灾的人员的生命将处于危险之中,因为可能会导致烧伤。在真实的火灾场景中,最重要的是确保建筑物内人员的生存,同时确保救援队伍自身在灭火过程中的安全,并以最短的时间完成任务。仅仅两分钟内,火灾就可能变得致命,而五分钟内,住宅就可能被火焰吞噬[11],这就是为什么快速性能必须优先考虑的原因。
当人员处于恐慌状态时,对突发事件的反应时间会变慢。这可能导致在火灾发生的情况下,人员需要过长时间才能开始寻找逃生路线,很多时候恐慌本身会导致人员无法逃脱,被困于火灾中直至死亡或窒息。然而,计算机不会恐慌,这使得它们能够在几秒钟内计算出一条逃生路线,从而有可能提高被困人员的生存几率,因为这能够提升消防部门的快速响应性能。
本研究的目的是在先前创建的场景中,测量概率路线图(PRM)和A*算法在模拟环境下的响应时间。通过该研究,旨在找到能够在最短时间内生成安全输出的算法。衡量算法性能的一个典型指标是使用兰道符号(通常称为大O符号),其形式化定义如下:
$$
O(g(x))={ f(x): \text{exist } x_0, c> 0 \text{ such that } \forall x>= x_0> 0: 0<= |f(x)| <= c|g(x)|}
$$
(1)
这种算法分析方法可用于度量算法复杂度,尽管它是计算机科学中广泛使用的一种分析方法,但该方法往往对非递归算法给出有利的结果。然而,在某些情况下,一个按Landau分析复杂度较低的非递归算法,在实践中可能会被一个递归算法超越。
针对此问题,选择了一种基于运行时间和正向结果的方法。该方法包括测量算法在给定环境中读取、计算并生成从A点到B点路径所需的时间。上述算法已在不同场景中进行了测试,这些场景根据其复杂度级别进行划分,即在墙壁数量由少到多的不同场景中模拟火灾。执行算法分析的步骤如下:
- 将一个矩阵(图像)提供给算法并进行处理。
- 计时器启动
- 算法处理矩阵,并寻找一条从给定点到另一点(A‐B)避开火灾的最优路径。
- 算法获得最优路径,并将其写入矩阵(图像)中。
- 计时器结束

这些步骤在下一节中详细说明。同样,这些比较的结果也已呈现。
在第2节中介绍了一些相关工作,在第3节中展示了分析方法,在第4节中呈现了工作结果,最后在第5节中得出了本工作的结论。
2 相关工作
如今,由于机器人和人工智能的使用日益增多,仿真应用也不断增长,而现实生活中的某些设备和设置成本较高[12]。场景可以是静态的,即只有场景本身是唯一的变量;也可以是动态的,即在人工智能代理执行过程中存在物体在场景中移动。在某些情况下,新算法的创建和测试可能成本高昂。在真实场景中进行可能需要占用大量空间或消耗大量材料。
幸运的是,如今存在两种进行仿真的方法,即通过数据集或仿真软件。
数据集是包含地图数据或传感器数据的原始数据,可用于复现实验,但数据集属于静态数据。互联网上有不同的数据集可供实验使用,例如存在像MRPT这样包含经过充分测试的应用程序和库(涵盖数据结构[10])的数据集,或像MAPIR这样通过4个RGB‐D传感器和一个2D激光扫描仪创建的数据集[15]。
另一方面,我们有能够进行动态仿真的仿真软件。存在不同类型的模拟器,例如简易二维机器人模拟器 STDR[16],可创建2D地图;MORSE模块化开放机器人仿真引擎[4],是一种用于学术机器人的通用模拟器;V‐REP[14],是一种多功能且可扩展的机器人仿真框架。一些模拟器可以进行逼真的仿真,例如 Gazebo[1],它使用SDF[5]文件来描述三维世界,并可在其中进行各种类型的动态仿真。仿真软件可用于模拟不同情况,其中一种情况就是火灾。存在室外火灾模拟器,其中甚至已进行了一些建模工作,可以预测野火概率[3]。Hasan等人在[8]中提到,尽管已有能够执行火灾探测的成熟系统,但火灾误报仍然是需要改进的挑战。目前有许多关于通过智能系统进行火灾探测的研究。目前使用图像处理系统,通过报警系统通知人员。这些系统能够向处于潜在危险中的用户以及消防站发送消息。林等人[7]、坎迪尔等人[6]、艾马兹[2]和A.G 罗亚‐博尔博拉[13]展示了使用室内火灾模拟器的优势。从缩短疏散时间到逃生路径规划均已得到验证。然而,在上述研究中,所使用的路径规划算法均为广为人知且易于实现的算法,特别是在[13]中使用了A*算法。当时间是关键变量时,这些算法有时并非最佳选择。
3 材料与方法
实验使用一台安装了Linux操作系统的戴尔 Latitude E5450计算机进行。该计算机配备8 GB内存和英特尔酷睿i7‐5600U处理器。此处提到的测试均在 Python3.8编程语言中完成。
3.1 环境准备
本研究中使用的场景是通过[12]中解释的方法创建的,火灾仿真则是使用[13]中解释的方法完成的。下一行解释了该过程的摘要。
场景构建通过为场景中的每面墙壁分配类型(无、完整或带门墙壁 [左 ‐ 右])来实现,该场景是一个网格 Gij, i ∈{1,…, M}, j ∈{1,…, N},其中包含(M ×(N − 1))横向墙壁 Hij, i ∈{1,…, M}, j ∈{1,…, N − 1}和 N ×(M − 1)纵向墙壁 Vij, i ∈{1,…, N},j ∈{1,…, M − 1}。先构建横向墙壁,再构建纵向墙壁。所有有限的墙壁均为完整墙壁。
使用独立概率来构建内部墙壁。a priori选择墙壁类型Wk k ∈{1, 2, 3, 4}的概率 P(wk)由公式2给出:
$$
P(wk) = \sum_{k=1}^{4} P(wk) = 1
$$
(2)
一旦构建完世界地图,就会以灰度图像的形式输入到算法中,该图像由一个大小为 M 和 N的矩阵表示。
生成了一张新图像,在该图像中,可燃烧的像素以其可能燃烧的程度来表示。像素的值根据室内火灾模拟器提供的图像中的值标记为0或1,对于被占据的黑色区域(值0表示灰度值为0的像素,意味着不可燃烧;1表示自由区域,由白色像素(灰度值为255)表示,意味着该像素可以被燃烧。
本作业采用一种概率方法进行分配,具体描述如下:对于室内火灾模拟器提供的图像I中自由空间内的每个像素,在逐像素扫描图像时,生成一个随机数 a ,其中 0< a< 1,然后在新图像 IP中赋值为IP(m, n) = 1,如果 a<= P 0;否则为其他情况。对于模拟器提供的图像中墙壁的每个像素,其火灾概率为零。
在此之后,创建一个起始点列表 P I=[X, Y],这些起始点作为输入传递给燃烧器。对于每个点火点,都会进行验证,以确认该点是否为图像中可燃的点,即 IP(x, y) = 1。创建一个点火点,并生成一个待燃点列表P Q= ∅。如果该点火点是易燃的,则仅当满足以下条件时才将其添加到可燃点列表中: IP(m, n) ∈/ P Q;然后检查最近添加点的相邻点,若其可点燃,则将其加入待燃点列表。此后,点火列表向前推进一步。
3.2 测试执行
需要注意的是,整个过程是根据执行时间而非处理器时间来测量的,这意味着从算法开始到结束的总耗时被记录下来,而不考虑内部处理器空闲、内存负载或其他操作系统进程的影响。运行比较的过程如下所述:[13]中所示的场景创建器生成若干不同类型场景,随后将地图以图像形式提供给室内火灾模拟器,火灾模拟器生成一系列图像,表示火灾在每个时刻的蔓延情况,直到火势无法继续蔓延为止。每次由室内火灾模拟(矩阵)生成的图像都会输入给算法,这些图像代表特定时刻的火灾蔓延状态、墙壁以及自由空间。输入图像会被转换为灰度图像,其中等于255的值表示自由空间(即无火灾区域),也就是可以构建路径的空间。火势蔓延区域和阻碍路径构建的像素(墙壁)被标记为0,这些是算法必须避开的像素。对于每张图像:
- 图像已加载
- 计时器已启动
- 算法已启动
-
一旦算法找到路径:
– 计时器已停止
– 计算结束时间和开始时间之间的差值
– 在火灾实例(图像)中绘制路径
– 将时间写入CSV文件 - 验证是否存在另一张图像
- 如果存在,则重新启动该过程
存在一组世界 W,对每个wi进行一组测试 T(从初始火灾点燃到火灾无法继续蔓延的时间),然后将每次单独的测试 tj保存在csv文件中,供后续进行数据分析。
数据分析分为以下两个部分进行:
每个世界路径规划所用的平均时间为 wi,其计算方式如下:
$$
\frac{\sum_{t=1}^{j} t_j}{j}
$$
然后通过以下方式进行第二次分析:
$$
\frac{\sum_{w=1}^{i}\sum_{t=1}^{j} w_{ij}}{i \ast j}
$$
4 结果
本工作的结果已以一种便捷的方式呈现为图表,旨在清晰地展示整个过程完成所用时间及结果的可视化效果。这些图表展示了火灾发生时刻(火灾实例)、世界复杂度与算法时间之间的关系。为了更清楚地理解图表,从左到右依次为火灾实例,按火场面积从小到大排列(火势蔓延较多的场景),以及场景复杂度(从最简单的场景到墙壁较多的场景);从下到上则表示算法寻找逃生路线所花费的时间。
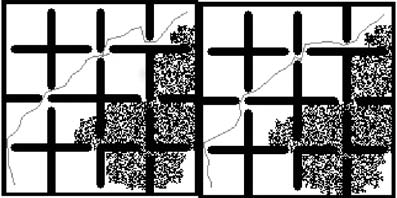
图像展示了PRM和A*算法在路径构建方式上的一些差异。
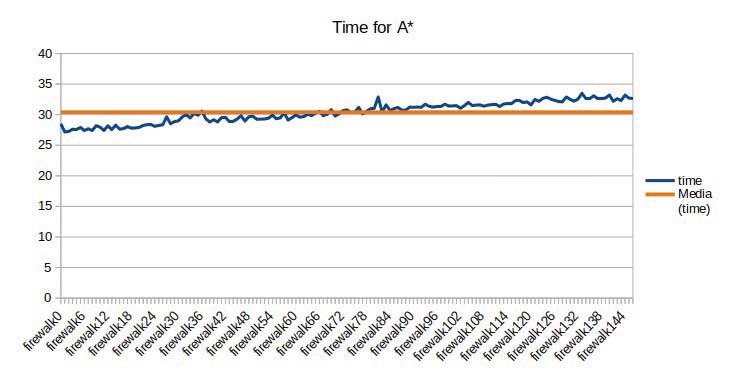
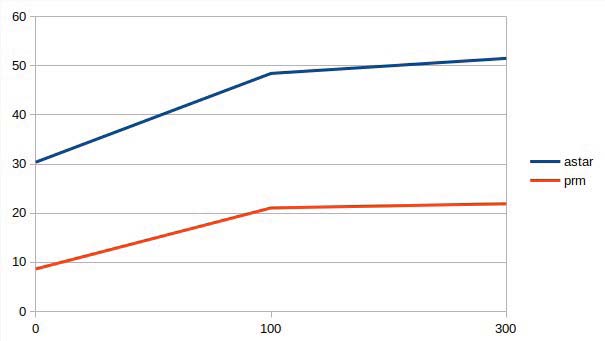
如图2和图3所示,可以注意到,随着墙壁数量的增加,A*算法所需时间更长。这意味着场景越复杂,火势蔓延越多,算法完成路径规划所需的时间就越长。需要注意的是,每次运行A*算法所生成的路径在距离上都接近最优路径。
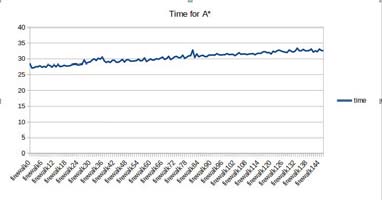
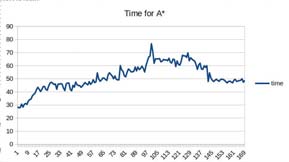
在第一个图表中,场景内墙壁较少,A*算法耗时介于25到35秒之间;在第二个场景墙壁较多的图表中,A*算法耗时介于28和80秒之间。这意味着场景越复杂,A*算法寻找路径所需的时间就越长。
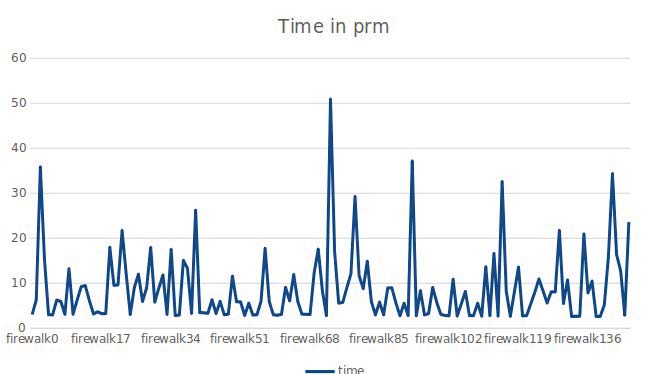
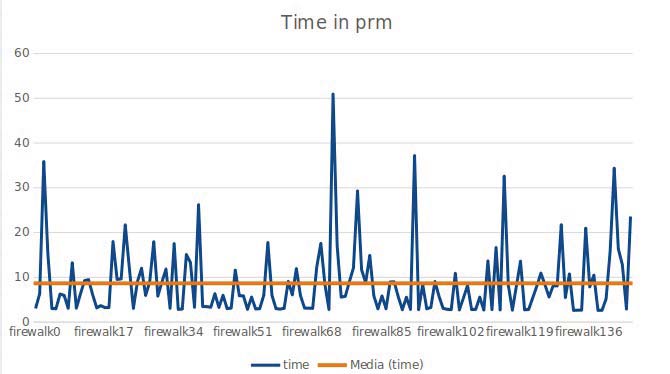
另一方面,PRM算法显示出一个从3到50秒的变化时间,这是由于该算法的概率特性所致。由于它基于随机点(伪随机)并由此生成路径,因此有可能在最初的几代中就找到路线,也有可能产生大量随机跳跃。这种算法的随机性导致其在同一场景中的行为发生变化,这种随机性可以在图4和图5中体现出来。
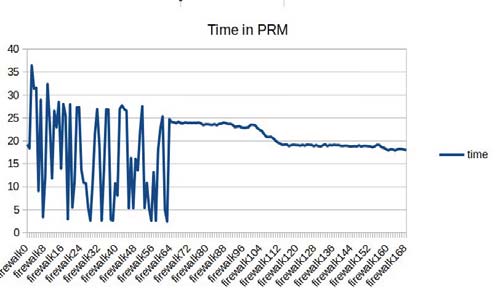
在第一个图表中,场景内较少墙壁,PRM耗时介于3到50秒之间;在第二个场景中,墙壁更多,PRM耗时介于3和35秒。这意味着由于PRM的概率特性,即使在复杂场景中时间有所增加,其变化也不像A*算法那样长。
可以看出,由于PRM算法具有随机性且运行时间不恒定,因此无法对算法进行直接比较,因为它没有表现出明显的时间趋势。众所周知,使用这种方法作为比较方式有时并不理想,因为异常值容易使其偏离正常结果。但在本例中,异常值不会影响该方法的使用,因为其目的是展示算法给出解决方案所需的总时间,因此对于房屋、竞技场或仓库等场景,该简单解决方案能够提供各算法定义解决方案所需时间的大致概念。
5 结论
最优路径或更好结果是一个广泛使用的术语,但它可能意味着许多不同的衡量标准,判断标准会因情况而异,有时是最短距离,有时是最短时间,有时是最大收益。
显然,在最短路径方面,A*算法更胜一筹,因为它始终计算最优路径,但这意味着需要大量的计算。
在某些情况下,使用一种广泛使用且易于实现的算法并不是最佳解决方案,因为在解决时间更为重要的场景中,需要一种能够在尽可能短的时间内解决问题的算法,而不论问题的复杂程度如何。在此情况下可以表明,PRM算法在应对室内火灾情况的解决时间方面表现更优,这可能成为一至多名人员生死之间的关键差异。
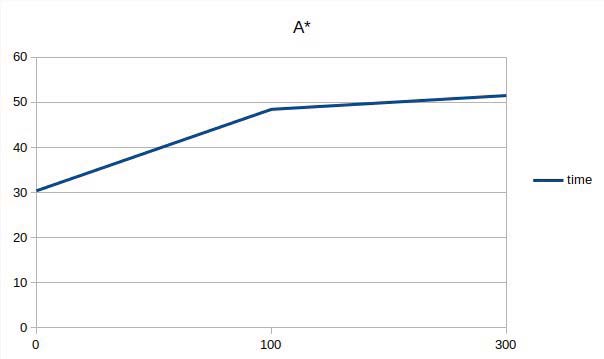
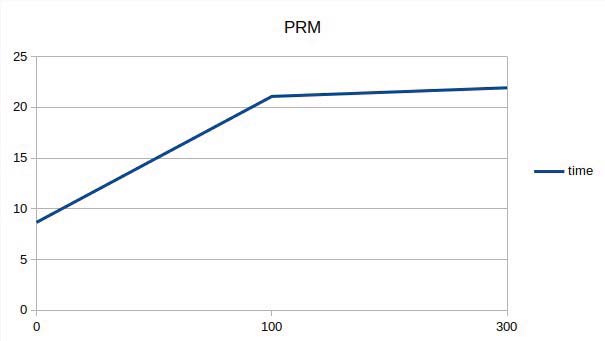
无论如何,可以看出PRM方法在时间上更具优势。如图8、9和10所示,场景越复杂、火势蔓延越严重,A*算法和PRM算法寻找路径所需的时间都会增加,但PRM算法的时间增长斜率小于A*算法。这意味着在非常复杂的场景中,如果优先考虑获取解决方案的时间,则不建议使用A*算法。
到火灾的距离以及与其他一些人工智能技术在进行仿真时的兼容性。
这一结论的一个示例见图11(b),其中尽管是不同的实验,但与图1相比,路线与火灾之间的距离有所改善。
此外,在图11中可以注意到,A*算法在距离上优于PRM,但在时间上,PRM的性能更优,如图表所示。




















 722
722

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








