推导 模型矩阵的逆转置矩阵求运动物体的法向量

一个物体表面的法向量如何随着物体的坐标变换而改变，取决于变换的类型。使用逆转置矩阵，可以安全地解决该问题，而无须陷入过度复杂的计算中。

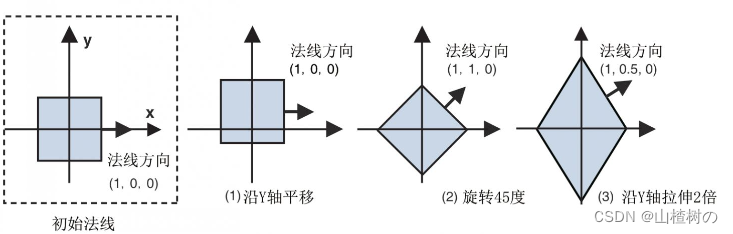
法向量变化规律

1. 平移变换不会改变法向量，因为平移不会改变物体的方向。 
2. 旋转变换会改变法向量，因为旋转改变了物体的方向。
3. 缩放变换对法向量的影响较为复杂。如上图，最右侧的图显示了立方体先旋转了45度，再在y轴上拉伸至原来的2倍的情况。此时法向量改变了，因为表面的朝向改变了。但是，如果缩放比例在所有的轴上都一致的话，那么法向量就不会变化。

模型矩阵的逆转值矩阵可以用来变换法向量。实际上，在某些特殊情况下，可以通过模型矩阵来确定物体变换后的法向量。比如说，当物体在旋转时，可以用旋转矩阵直接乘以法向量，就能获得旋转后的法向量。总之，计算变换后的物体表面的法向量方向时，是求诸于模型矩阵自身，还是模型矩阵的逆转值矩阵，取决于模型矩阵中已经包含的变换类型（平移、旋转或缩放）。

直接通过模型矩阵自身求变换后的法向量。如果模型矩阵中已经包含了平移变换，法向量就会被当作顶点坐标平移，从而导致法向量与原有的表面朝向不一致。比如说，一个法向量是（1，0，0），沿Y轴平移2.0个单位后，就变成了（1，2，0）。事实上，如果你从4×4的模型矩阵的左上角抽出3×3的子矩阵，然后乘以法向量，就可以避免该问题。如下所示，4*4的模型矩阵：

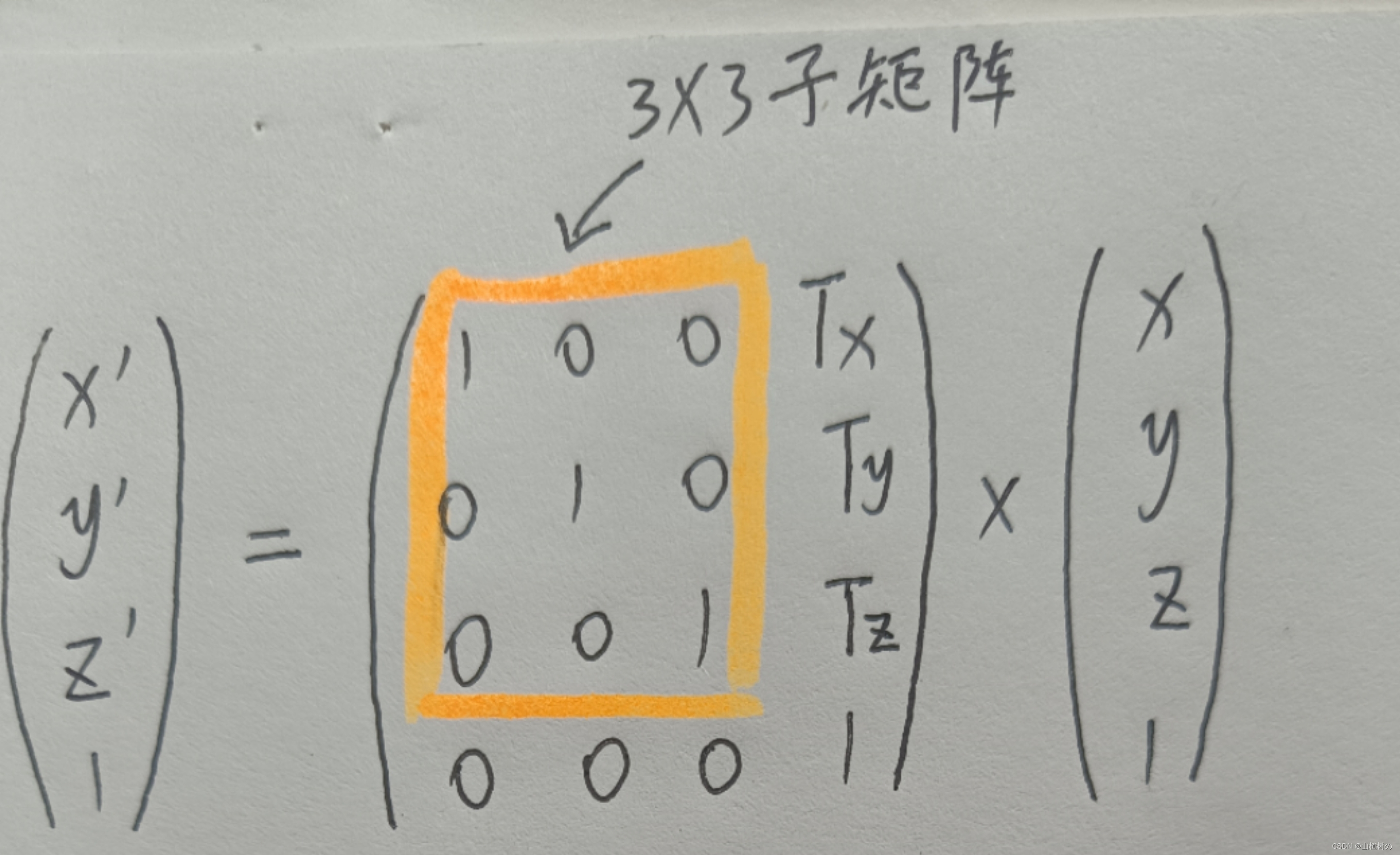
由于3×3的子矩阵实际上包含了旋转矩阵和缩放矩阵的信息，我们来逐一考虑。

• 如果只