【学习笔记】《滑模变结构控制MATLAB仿真基本理论与设计方法》（刘金琨）--第一章

原创已于 2023-11-16 15:43:32 修改 · 1.3k 阅读

7 ·

CC 4.0 BY-SA版权

文章标签：

#学习 #笔记

于 2023-11-16 15:39:18 首次发布

本文详细介绍了滑模变结构控制的基本原理，包括其控制策略的不连续性，数学表达形式，滑模面设计，以及针对不确定因素的优化。还提到了MATLABSimulink在仿真实现中的关键作用。

本章主要介绍滑模变结构的基本原理及应用领域，重点在把握滑模变结构控制的原理，基本滑模面的设计。接下来将以问题形式层层递进，介绍本章。

一、什么是滑模变结构控制？

让我们看看书上的原话：

是变结构控制系统的一种控制策略。与常规控制的区别在控制的不连续性，即一种使系统“结构”随时间变化的开关特性。该控制特性可以使系统在一定特性下沿规定的状态轨迹做小幅度、高频率的上下运动，即所谓的“滑模”运动。

那么很自然地引出下一个问题，作为控制领域从业者，我们关心的是某个控制律的具体数学形式。

二、滑模数学表达

首先考虑定义中的控制律可以使系统沿规定的状态轨迹做小幅度运动，这句话藏了两层意思：如何使系统沿设计的状态运动？以及沿什么样的状态运动？这就将其拆分为了两个问题。考虑一个超曲面s，它将状态空间切割为两部分：s>0和s<0。在切换面s=0上的运动点有三种情况：

（1）通常点--系统运动到切换面附近穿越而过。（点A）

（2）起始点--系统运动到切换面附近时，向切换面两边离开。（点B）

（3）终止点--系统运动到切换面附近时，从两侧趋向该点。（点C）

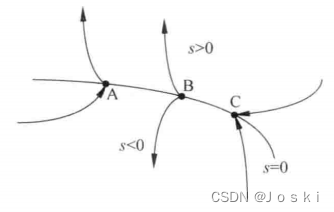
在滑膜变结构中，我们关心终止点，若一个区域内所有点都是终止点，运动点趋近该区域时，就会被“吸引”在该区域内运动。这种区域就叫做滑模区。

根据此定义，显然，在切换面附近的 $s>0$ 的区域，需要满足 $\dot{s}<0$ ；在 $s<0$ 的区域，需要满足 $\dot{s}>0$ 。用极限表达为 $\lim_{s\to 0}s\dot{s}<0$ 。

推到这里，对Lypunov函数敏感的同学应该发现，我们可以构造Lypunov函数 $V=s^{2}$ ， $V$ 自然是半正定的，只需证明 $\dot{V}=2s\dot{s}\leq 0$ ，系统就稳定于 $s=0$ 。也就是说只要满足 $\lim_{s\to 0}s\dot{s}<0$ ，系统就稳定在 $s=0$ 。

根据以上讨论，滑模变结构控制的问题就可以归纳如下了：

（1）滑动模态存在，即针对 $s$ 的不同区域，有不同的控制律使其趋近切换面。

（2）满足可达性，即切换面以外的所有点都可以在有限时间内趋近切换面。

（3）保证滑模控制系统稳定。

（4）达到控制系统动态品质要求。

三、滑模面的一般设计形式

针对线性系统的一般模型 $\dot{x}=Ax+Bu$ ，滑模面设计为

$s(x)=C^{\mathbf{T}}x=\sum_{i=1}^{n}c_{i}x_{i}=\sum_{i=1}^{n-1}c_{i}x_{i}+x_{n}.$

其中， $x$ 为状态向量， $C=\left [ c_{1} ,c_{2} ... c_{n-1},1\right ]^{\mathbf{T}}$ 。为保证系统稳定，应使Laplace算子 $p$ 满足： $p^{n-1}+c_{n-1}p^{n-2}+...+c_{2}p+c_{1}$ 是Hurwitz。这是老生常谈的稳定性判据了，也就是通过判断特征方程的特征根正负来判断系统稳定性。

四、滑膜变结构的优化方向

该书之后的章节，针对不确定参数扰动、时滞、离散时间等问题提出了不同的控制律，也就是在如何到达滑模面这一问题做出优化。其不连续的开关特性会导致系统产生抖震，消抖也是设计时需要考虑的问题之一。本书收录了趋近律方法进行自适应调整消抖，后续章节将会出现。其余书中提及内容请参阅原著。

五、仿真说明

本书中的仿真均是采用MATLAB中的Simulink环境实现，因此，s函数的设计是最重要的一环。本书中s函数主体包含三个部分：initialization（初始化）函数、mdlDerivation（微分方程模型）函数、mdlOutput（输出）函数。更多函数结构参见具体示例。书中的初始化函数使用size.的结构体形式表示相关变量，便于阅读和修改。在mdlDerivation中，注意将模型按阶次顺序写成多微分方程形式，使用ode45、ode23等函数进行求解。