【数组】相关类型题目整理[一]

一、二维数组中的查找

（一）双重循环枚举遍历

这个思路太简单了，这里就不需要再多说了。代码如下：

class Solution 
{
public:
    bool Find(int target, vector<vector<int> > array)
     {
        for(int i=0;i<array.size();i++)
        {
            for(int j=0;j<array[i].size();j++)
            {
                if(array[i][j]==target)
                {
                    return true;
                }
            }
        }
        return false;
    }
};

（二）通过数组行列递增的特点简化双重循环

思路可以通过下图很清楚的看到
自己给这种方法取名叫【二维二分法查找】

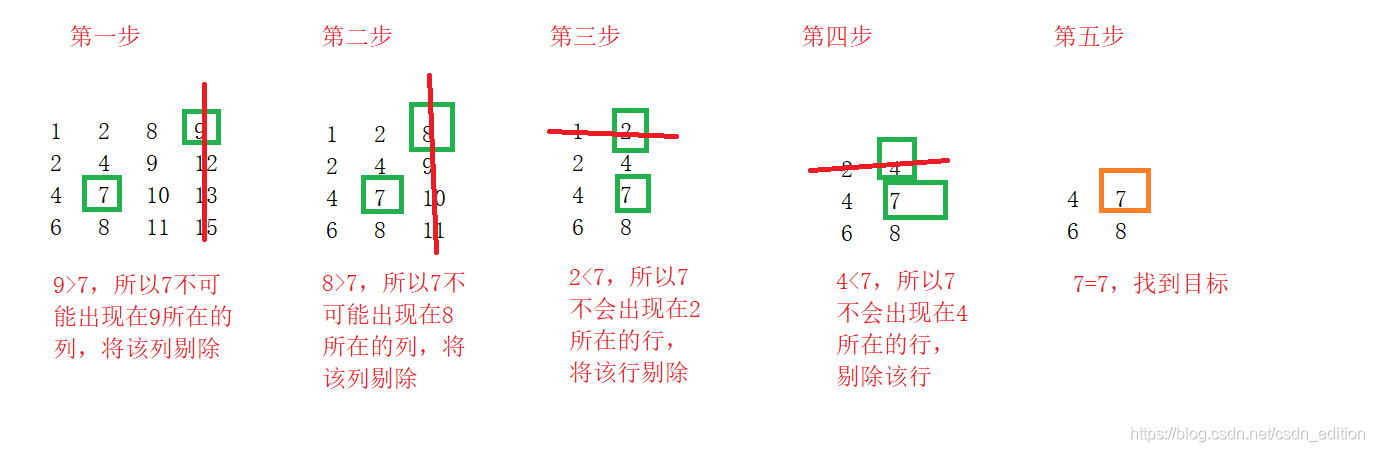
代码如下：

class Solution
 {
public:
    bool Find(int target, vector<vector<int> > array) 
    {
        int i=0;
        int j=array[0].size()-1;
        int m=array.size();
        while(i<m && j>=0)
        {
            if(array[i][j]==target)
            {
                return true;
            }
            else if(array[i][j] < target)
            {
                i++;
            }
            else
            {
                 j--;
            }
        }
        return false;
    }
};

二、斐波那契数列

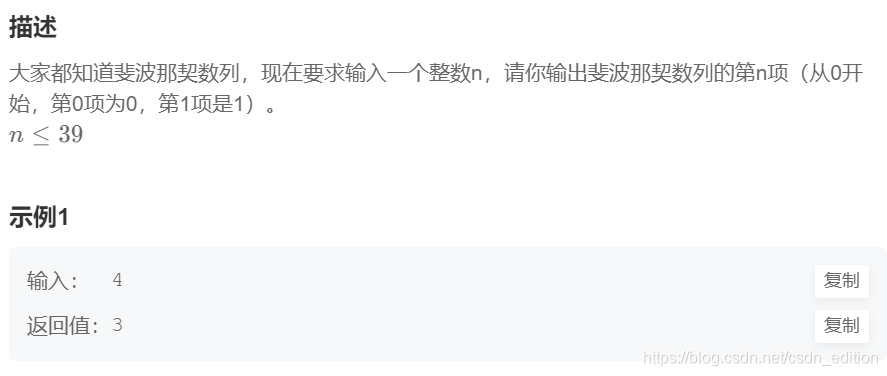
（一）常规解法

斐波那契数列：1 1 2 3 5 8 11…

代码如下：

class Solution {
public:
    int Fibonacci(int n) {
        if(n==0)
        {
            return 0;
        }
        if(n==1 || n==2)
        {
            return 1;
        }
        int f1=1;
        int f2=1;
        int f3=0;
        for(int i=3;i<=n;i++)
        {
            f3=f1+f2;
            f1=f2;
            f2=f3;
        }
        return f3;
    }
};

（二）递归解法

代码如下：

class Solution {
public:
    int Fibonacci(int n) {
        if(n==0)
        {
            return 0;
        }
        if(n==1 || n==2)
        {
            return 1;
        }
        return Fibonacci(n-1)+Fibonacci(n-2);
    }
};

（三）动态规划

代码如下：

class Solution {
public:
    int Fibonacci(int n) {
        vector<int> dp(n+1,0);
        dp[1]=1;
        for(int i=2;i<=n;i++)
        {
            dp[i]=dp[i-1]+dp[i-2];
        }
        return dp[n];
    }
};

三、数组中出现次数超过一半的数

（一）通过sort()函数解决

代码如下：

class Solution 
{
public:
    int MoreThanHalfNum_Solution(vector<int> numbers) 
    {
        sort(numbers.begin(),numbers.end());
        return numbers[numbers.size()/2];
    }
};

（二）哈希表法

思路：将数组中的元素作为key，将元素出现的次数作为value，最终找到哈希表中的value值大于数组长度一半的key即可

代码如下：

class Solution 
{
public:
    int MoreThanHalfNum_Solution(vector<int> numbers) 
    {
        unordered_map<int,int> hash;
        for(int i=0;i<numbers.size();i++)
        {
            hash[numbers[i]]++;
        }
        
        for(auto &x:hash)
        {
            if(x.second>numbers.size()/2)
            {
                return x.first;
            }
        }
        return -1;
    }
};

• 时间复杂度和空间复杂度都为O(n)

（三）哈希表法的代码优化

代码如下：

class Solution 
{
public:
    int MoreThanHalfNum_Solution(vector<int> numbers) 
    {
        unordered_map<int,int> hash;
        for(int i=0;i<numbers.size();i++)
        {
            hash[numbers[i]]++;
            if(hash[numbers[i]] > numbers.size()/2)
            {
                return numbers[i];
            }
        }
        
        
        return -1;
    }
};

更多方法可以查看我的另外一篇博客https://blog.youkuaiyun.com/csdn_edition/article/details/109823297

四、调整数组顺序使奇数位于偶数前面

（一）常规解法：额外使用一个vector+两次遍历原vector

• 这种解法比较常规，也比较容易想的出来，时间复杂度和空间复杂度都为O(n)
• 代码如下：

class Solution {
public:
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param array int整型vector 
     * @return int整型vector
     */
    vector<int> reOrderArray(vector<int>& array) {
        // write code here
        int m=array.size();
        int j=0;
        vector<int> res(m,0);
        for(int i=0;i<m;i++)
        {
            if(array[i]%2!=0)
            {
                res[j++]=array[i];
            }
        }
        for(int i=0;i<m;i++)
        {
            if(array[i]%2==0)
            {
                res[j++]=array[i];
            }
        }
        return res;
    }
};

（二）不使用额外空间----双指针

思路如下图所示：

代码如下：

class Solution {
public:
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param array int整型vector 
     * @return int整型vector
     */
    vector<int> reOrderArray(vector<int>& array) {
        // write code here
        int i=0;
        for(int j=0;j<array.size();j++)
        {
            //如果是奇数
            if(array[j] % 2 != 0)
            {
                //先将奇数保存到一个临时变量中
                int tmp=array[j];
                //将该奇数和它前面一个奇数之间的偶数整体向右移动一个数组的位置
                for(int k=j-1;k>=i;k--)
                {
                    array[k+1]=array[k];
                }
                //让两个奇数相邻，让i指向第一个偶数的位置
                array[i++]=tmp;
            }
        }
        return array;
    }
};

总之，i指针一直指向数组的第一个偶数的位置

• 时间复杂度为O(n^2)，空间复杂度为O(1)

✨😊❤