HDU 1688 Sightseeing

最新推荐文章于 2020-08-02 10:43:16 发布

Crossing over

最新推荐文章于 2020-08-02 10:43:16 发布

阅读量223

点赞数

分类专栏：图论动态规划

本文链接：https://blog.youkuaiyun.com/coord_/article/details/89109890

版权

图论同时被 2 个专栏收录

67 篇文章

订阅专栏

动态规划

54 篇文章

订阅专栏

传送门

求次短路。给一个有向图，给定起点终点，求最短路条数和只比最短路的值大1的路径的条数之和。

这道题就是用普通的次短路求解就行了，求出来的次短路如果正好比最短路大1，那么就存在这道题中所谓的“大1次短路”；如果不是则就没有。

这道题比较人性化，说了几个关键信息。没有自边（自环），每条边的权值都是正数，可能有重边。
权值都是正数意味着没有零环和负环，因为有零环意味着求不出最短次短路径条数（或者在最短基础上要求边最多或点最多）。因为需要求次短，所以有重边意味着绝对不能用邻接矩阵。

有意思的是，这道题说两条路径是不同的当且仅当这两条路径包含的边集不等（不是边序列不同）。这个定义就有丶意思了，意味着走零环一次和多次都是相当于同一条路径。然而，这道题没有零环，不用考虑这些了。

下面说正题，求次短路需要两倍于最短路的求解时间，每个数组（d[],vis[],(num[])）都要分别设置两份，分别存储最短和次短版本，就像在dijkstra中，需要大循环2N次，每次确定一个d[]或d2[]。每次大循环是在两个数组中找全局最小值，无论是d[]还是d2[]。然后去更新邻接点的时候有四种情况：
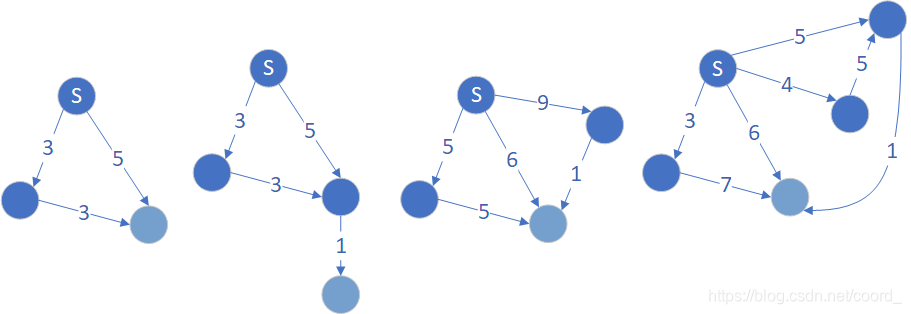
在这里插入图片描述
这四种情况介于最短和次短之间。需要说明的是以下两点：

每种情况其实都可以不加对vis的判断（基础dijkstra也一样，只是以前没注意过这个细节）。其实是可以不加的。因为根据dijkstra过程，可以看出每次中介点更新的点的d值都一定大于d[u]（只要权值都为正），所以每次大循环找到最小值不仅是当前的最小值，也是从此及以后的最小值。
所以在权值为正的情况下（权值不保证为正也用不了dijkstra。。）加上这个判断其实并无卵用，当然为了规范严谨可以加上。
在前两种情况下，最短路更小和最短路相等只能由中介点的最短路来更新，永远不可能由次短路更新！！ 因为次短路若有的话一定是通过最短路作为标杆才能判断出来的，最短路在前次短路在后，你自己想想，绝对不可能的。

那为什么后两种情况都能由最短和次短更新？因为有实锤，且看下图：
在这里插入图片描述


#include <cstdio>
#include <iostream>
#include <algorithm>
#include <vector>
#include <cstring>
#include <string>
#include <queue>
using namespace std;

const int INF = 1e9;
const int MAXN = 1001;
int N, M, T;
int S, E;

struct Edge
{
	int n, w;
};
vector<Edge> ve;
vector<int> v[MAXN];

int d[MAXN];
int d2[MAXN];
int num[MAXN];
int num2[MAXN];
bool vis[MAXN];
bool vis2[MAXN];

void init()
{
	ve.clear();
	for (int i = 1; i <= N; i++) v[i].clear();
}

void dijkstra()
{
	memset(num, 0, sizeof num);
	memset(num2, 0, sizeof num2);
	memset(vis, 0, sizeof vis);
	memset(vis2, 0, sizeof vis2);
	fill(d + 1, d + N + 1, INF);
	fill(d2 + 1, d2 + N + 1, INF);

	d[S] = 0;
	num[S] = 1;

	for (int iter = 1; iter <= N * 2; iter++)          //
	{
		int u = -1, mind = INF, id = 1;
		for (int i = 1; i <= N; i++)
		{
			if (!vis[i] && d[i] < mind)
			{
				mind = d[i];
				u = i;
			}
		}
		for (int i = 1; i <= N; i++)
		{
			if (!vis2[i] && d2[i] < mind)
			{
				mind = d2[i];
				u = i;
				id = 2;
			}
		}

		//if (id == 2 && u == E) return;           这句加上也不会错。
		if (u == -1) return;                       // 必须加这一句，因为d2[E]可能永远是INF

		if (id == 1) vis[u] = true;
		else vis2[u] = true;

		for (int i = 0; i < v[u].size(); i++)
		{
			int n = ve[v[u][i]].n;
			int w = ve[v[u][i]].w;
			if (/*!vis[n] && */mind + w < d[n])
			{
				d2[n] = d[n];
				num2[n] = num[n];
				d[n] = mind + w;
				//num[n] = id == 1 ? num[u] : num2[u];
				num[n] = num[u];
			}
			else if (/*!vis[n] && */mind + w == d[n])
			{
				//num[n] += id == 1 ? num[u] : num2[u];
				num[n] += num[u];
			}
			else if (/*!vis2[n] && */mind + w < d2[n])
			{
				d2[n] = mind + w;
				num2[n] = id == 1 ? num[u] : num2[u];
			}
			else if (/*!vis2[n] && */mind + w == d2[n])
			{
				num2[n] += id == 1 ? num[u] : num2[u];
			}
		}
	}
}

int main()
{
	//freopen("data.txt", "r", stdin);
	int a, b, c;
	scanf("%d", &T);
	for (; T--;)
	{
		scanf("%d%d", &N, &M);
		init();
		for (int i = 0; i < M; i++)
		{
			scanf("%d%d%d", &a, &b, &c);
			ve.push_back(Edge{ b,c });
			v[a].push_back(i);
		}
		scanf("%d%d", &S, &E);

		dijkstra();
		if (d[E] + 1 == d2[E]) printf("%d\n", num[E] + num2[E]);
		else printf("%d\n", num[E]);
	}

	return 0;
}

又写了个优先队列优化的dijkstra，第一次写这个。首先这个题需要构造一个存三个数（因为多了个区分最短次短的标识）的Node，然后塞到priority_queue里面。而且一定要注意第一种情况是需要把d[]和d2[]两个值都同时塞进去的。还要一定记住结构体内运算符重载函数的写法！（单个参数，结尾const修饰，和排序cmp函数的不同）


#include <cstdio>
#include <iostream>
#include <algorithm>
#include <vector>
#include <cstring>
#include <string>
#include <queue>
using namespace std;

const int INF = 1e9;
const int MAXN = 1001;
int N, M, T;
int S, E;

struct Edge
{
	int n, w;
};
vector<Edge> ve;
vector<int> v[MAXN];

struct Node
{
	int n, d, id;                                                  // id
	bool operator<(const Node& n0) const                           // 结尾的const必须加，不然编译错误
	{                                                              // 这个函数只能一个参数
		return d > n0.d;                                           // 这样是最小值在堆顶最前面，与排序相反
	}
};

int d[MAXN];
int d2[MAXN];
int num[MAXN];
int num2[MAXN];
bool vis[MAXN];
bool vis2[MAXN];

void init()
{
	ve.clear();
	for (int i = 1; i <= N; i++) v[i].clear();
}

void dijkstra()
{
	memset(num, 0, sizeof num);
	memset(num2, 0, sizeof num2);
	memset(vis, 0, sizeof vis);
	memset(vis2, 0, sizeof vis2);
	fill(d + 1, d + N + 1, INF);
	fill(d2 + 1, d2 + N + 1, INF);

	d[S] = 0;
	num[S] = 1;

	priority_queue<Node> p_q;
	p_q.push(Node{ S,d[S],1 });                                              // 别忘了加

	for (; !p_q.empty();)                                                    //
	{
		Node u = p_q.top();
		p_q.pop();

		if (u.d == INF) continue;                                            // 加不加都行，这样更严谨
		if (u.id == 1 && vis[u.n] || u.id == 2 && vis2[u.n]) continue;       //

		if (u.id == 1) vis[u.n] = true;
		else vis2[u.n] = true;

		for (int i = 0; i < v[u.n].size(); i++)
		{
			int n = ve[v[u.n][i]].n;
			int w = ve[v[u.n][i]].w;
			if (/*!vis[n] && */u.d + w < d[n])
			{
				d2[n] = d[n];
				num2[n] = num[n];
				d[n] = u.d + w;
				//num[n] = id == 1 ? num[u] : num2[u];
				num[n] = num[u.n];

				p_q.push(Node{ n,d2[n],2 });                                  这种情况要push两个！
				p_q.push(Node{ n,d[n],1 });                                  //
			}
			else if (/*!vis[n] && */u.d + w == d[n])
			{
				//num[n] += id == 1 ? num[u] : num2[u];
				num[n] += num[u.n];
			}
			else if (/*!vis2[n] && */u.d + w < d2[n])
			{
				d2[n] = u.d + w;
				num2[n] = u.id == 1 ? num[u.n] : num2[u.n];

				p_q.push(Node{ n,d2[n],2 });                                 //
			}
			else if (/*!vis2[n] && */u.d + w == d2[n])
			{
				num2[n] += u.id == 1 ? num[u.n] : num2[u.n];
			}
		}
	}
}

int main()
{
	//freopen("data.txt", "r", stdin);
	int a, b, c;
	scanf("%d", &T);
	for (; T--;)
	{
		scanf("%d%d", &N, &M);
		init();
		for (int i = 0; i < M; i++)
		{
			scanf("%d%d%d", &a, &b, &c);
			ve.push_back(Edge{ b,c });
			v[a].push_back(i);
		}
		scanf("%d%d", &S, &E);

		dijkstra();
		if (d[E] + 1 == d2[E]) printf("%d\n", num[E] + num2[E]);
		else printf("%d\n", num[E]);
	}

	return 0;
}