【MATLAB代码】TDOA（到达时间差）定位|使用两步加权最小二乘，定位二维目标、4个锚点，附代码下载链接

本代码实现了一种高精度二维目标定位算法，基于到达时间差（TDOA）测量，结合两步加权最小二乘法（Two-Step WLS），利用4个固定锚点（基站）的观测数据，估计移动目标的坐标。算法通过粗迭代和细迭代优化，显著降低测量噪声对定位精度的影响，适用于室内定位、无线传感器网络等场景。

代码介绍

算法原理

1. TDOA建模：

   • 距离差计算：通过信号到达各基站的时间差（TDOA）计算距离差，公式为$R_i=c\cdot \Delta t_i$，其中$c$为光速，$\Delta t_i$为时间差。
   • 噪声模拟：添加高斯噪声（标准差由 std_var1 控制）模拟实际测量误差。

2. 两步加权最小二乘：

   • 粗迭代：构造线性方程组$Ga\cdot u=h$，通过初始猜测（锚点位置均值）求解初步位置估计$u^{\ast }$。
   • 细迭代：引入加权矩阵$W$修正误差，优化方程为$A\cdot \delta u^{\ast }=h_2$，最终得到高精度估计$u_{\text{est}}$。

代码结构解析

1. 初始化：

   stations_position = 50 + 100*randn(4,2);  % 生成4个随机锚点坐标（均值为50，标准差100）
   position = 0*ones(1,2) + 5*randn(1,2);   % 生成待测点坐标（均值为原点，标准差5）
   

   • 基站与目标位置均通过随机生成，模拟实际部署场景。

2. TDOA观测建模：

   delta_t = r_ideal/c + std_var1*randn(size(r_ideal));  % 添加时间测量噪声
   r = delta_t*c;  % 转换为距离观测值
   R = Ri - R1;    % 计算基站间距离差
   

3. 迭代优化：

   • 粗迭代：快速收敛至粗略解，避免局部最优。
   • 细迭代：通过加权矩阵$W=(BQ{B}^T{)}^{-1}$抑制噪声，提升精度。

4. 可视化与输出：

   • 绘制锚点（红色*）、真实位置（黑色○）、估计位置（蓝色点）。
   • 输出坐标误差及欧氏距离误差。

应用场景

• 室内定位系统：商场、仓库中的资产追踪。
• 紧急救援：通过无人机基站快速定位被困人员。
• 工业物联网：工厂内设备或机器人的实时位置监控。

扩展与改进建议

1. 三维扩展：修改坐标维度，引入高度信息（参考：【MATLAB定位例程】TDOA（到达时间差）的chan-tylor，三维环境，附完整代码）
2. 动态目标追踪：结合卡尔曼滤波（EKF/UKF）处理移动目标（参考【MATLAB例程】基于TDOA定位（两步最小二乘）的三维轨迹定位和UKF滤波，TDOA的锚点可以自适应，附完整代码和代码详解）。
3. 多锚点支持：扩展代码支持更多基站（需调整矩阵维度及方程组构造逻辑）。参考：【MATLAB代码】二维平面上的TDOA，使用加权最小二乘法，不限制锚点数量，代码可复制粘贴

运行结果

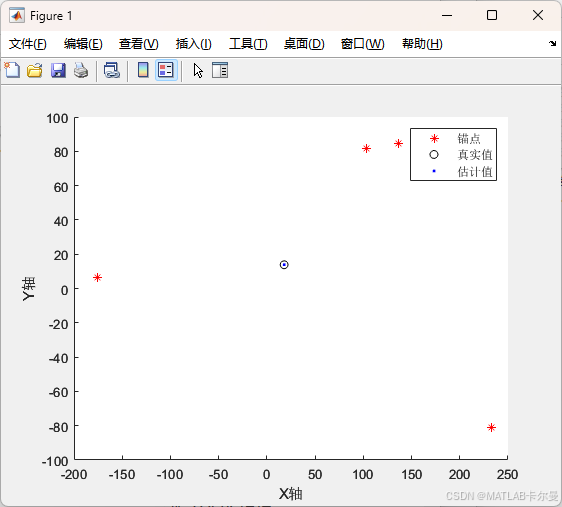
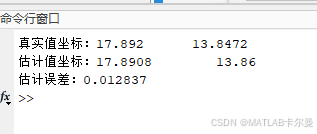
MATLAB代码

部分代码示例：

% 两步加权最小二乘，定位二维目标、4个锚点
% 2024-11-07/Ver1
%% 初始化
clc;clear;close all;
rng(0);
% 定义参数和待测点位置
std_var1 = 1e-11; %TDOA误差
% 固定基站位置
stations_position = 50+100*randn(4,2);
c = 3e8;
% 生成待测点坐标
position = 0*ones(1,2)+5*randn(1,2);
% TDOA 建模
delta = ones(4,1)*position - stations_position; %未知点与各基站之间的相对位置（矢量）
r_ideal = (sum(delta.^2,2)).^(1/2); %计算移动台到各个基站的实际距离（标量）
delta_t = r_ideal/c+std_var1*randn(size(r_ideal));
r = delta_t*c;

完整代码下载链接：https://download.youkuaiyun.com/download/callmeup/90631434

如需帮助，或有导航、定位滤波相关的代码定制需求，请点击下方卡片联系作者