UWB室内定位移动站距离数据波动处理全解析——Allan方差分析、样条拟合与快速卡尔曼滤波

引言：随着物联网技术的飞速发展，室内定位需求日益增长，如智慧工厂、仓储物流、智慧医疗等场景。超宽带（UWB）技术凭借其定位精度高、抗干扰能力强、穿透性好等优势，成为室内定位领域的主流技术之一。然而，在实际应用中，UWB室内定位移动站测量的距离数据不可避免地存在波动，这会严重影响定位精度。本文将从UWB距离数据波动的根源出发，详细剖析数据波动特性，重点围绕Allan方差数据统计、数据样条拟合、快速卡尔曼滤波三种核心数据处理方法，深入讲解其原理、软件算法实现，并搭配流程图直观呈现处理流程。全文采用大量表格对比不同技术的优劣、参数差异及适用场景，力求内容通俗易懂、逻辑清晰，为相关工程技术人员提供全面的技术参考。

一、UWB室内定位移动站距离测量基础

1.1 UWB技术定位原理

UWB技术是一种无载波通信技术，通过发送和接收纳秒级的极窄脉冲来传输数据。其定位核心原理是基于距离测量，再通过多边定位、三角定位等算法计算移动站的位置。常见的UWB距离测量方法主要有两种：飞行时间（TOF）法和到达时间差（TDOA）法。

测量方法	核心原理	优势	劣势	适用场景
飞行时间（TOF）法	测量UWB信号从移动站发送到基站再反射回移动站的总时间，结合光速计算距离（距离=光速×飞行时间/2）	定位精度高，直接测量距离，计算简单	对时钟同步要求高，易受多径效应影响	短距离高精度定位场景，如室内机器人定位
到达时间差（TDOA）法	测量UWB信号到达两个不同基站的时间差，通过多个时间差构建方程组求解移动站位置	无需移动站与基站严格同步，系统复杂度较低	定位精度受基站布局影响大，需要更多基站支撑	大面积室内定位场景，如大型仓储、购物中心

1.2 移动站距离测量数据的构成

UWB移动站测量的距离数据并非真实距离的直接反映，而是由真实距离、系统误差、随机误差三部分组成，其数学表达式可表示为：

其中，D_meas为测量距离，D_true为真实距离，E_sys为系统误差，E_ran为随机误差。系统误差是由硬件设备、环境因素等固定因素引起的，具有可重复性和可修正性；随机误差是由噪声、多径效应等随机因素引起的，具有随机性和不可预测性，也是导致距离数据波动的主要原因。

1.3 距离数据波动的核心影响因素

UWB室内定位移动站距离数据波动的影响因素众多，可分为内部因素和外部因素两大类。内部因素主要与设备本身相关，外部因素则与定位环境相关。

因素类型	具体因素	波动影响机制	影响程度	缓解措施
内部因素	时钟漂移	移动站和基站的时钟精度不足，导致时间测量误差，进而引入距离测量波动	★★★★☆	采用高精度晶振，定期进行时钟同步校准
	电路噪声	接收电路中的热噪声、散粒噪声等会干扰信号检测，导致时间测量偏差，产生随机波动	★★★☆☆	优化电路设计，增加滤波电路，提高信号信噪比
	天线性能	天线增益不均匀、辐射方向图畸变，导致信号传输损耗不稳定，影响距离测量	★★☆☆☆	选用高性能UWB天线，合理布局天线位置
	功率波动	发射功率不稳定导致信号传播距离变化，引入距离测量误差	★★☆☆☆	采用功率稳定电路，实时监测发射功率
外部因素	多径效应	UWB信号在室内传播过程中遇到墙壁、家具等障碍物产生反射、折射，形成多径信号，接收端难以准确识别直达波，导致时间测量偏差	★★★★★	采用多径分辨算法，优化基站布局，避开障碍物密集区域
	遮挡物影响	移动站与基站之间被人体、设备等遮挡，导致信号衰减严重，测量距离出现跳变	★★★☆☆	增加基站数量，保证信号覆盖无死角，采用抗遮挡能力强的UWB模块
	环境噪声	室内其他无线设备（如Wi-Fi、蓝牙）产生的电磁干扰，干扰UWB信号接收，引入波动	★★☆☆☆	选择合适的UWB工作频段，采用跳频技术，增强抗干扰能力
	温度湿度变化	温度湿度变化会影响电磁波传播速度，进而影响距离测量精度，产生缓慢波动	★★☆☆☆	引入温度湿度补偿算法，实时修正传播速度

二、UWB距离数据波动特性分析

2.1 数据采集实验设计

为了准确分析UWB距离数据的波动特性，设计如下采集实验：

2.1.1 实验环境

实验地点选择典型的办公室内环境，面积约50㎡，室内包含办公桌、文件柜、沙发等障碍物，环境温度25℃，湿度60%。

2.1.2 实验设备

设备类型	型号	主要参数	数量
UWB基站	Decawave DW1000	工作频段3.5-6.5GHz，测量精度±10cm，通信速率110kbps-6.8Mbps	4个
UWB移动站	Decawave DW1000开发板	与基站参数匹配，支持TOF/TDOA测量	1个
上位机	联想拯救者Y9000P	Intel i7-12700H，16GB内存，512GB固态硬盘	1台
数据采集软件	自定义开发（基于Python）	支持数据实时采集、存储、可视化，采样频率可配置	1套

2.1.3 实验方案

1. 基站布局：将4个UWB基站固定在室内四周，确保基站之间无遮挡，且能覆盖整个实验区域，记录每个基站的精确坐标。

2. 移动站固定：将移动站固定在距离其中一个基站5m的位置，确保移动站与基站之间无遮挡（直射场景），同时在移动站与基站之间放置障碍物（遮挡场景）进行对比实验。

3. 数据采集：设置采样频率为100Hz，分别在直射场景和遮挡场景下采集距离数据，每个场景采集10000个数据点，数据存储为CSV格式，包含时间戳、测量距离、基站ID等信息。

2.2 波动特性统计指标

为了量化分析距离数据的波动特性，引入以下常用统计指标：

统计指标	数学表达式	物理意义	计算方法
均值	barD = frac{1}N\sum_{i=1}^{N}D_i\)	反映距离测量数据的中心趋势，接近真实距离	所有测量数据的算术平均值
方差（Variance）	sigma^2 = frac{1}{N-1}sum_{i=1}^{N}(D_i - bar{D})^2	反映数据偏离均值的程度，方差越大，波动越剧烈	每个数据与均值差的平方和除以（数据量-1）
标准差（Standard Deviation）	sigma = \sqrt{\frac{1}{N-1}\sum_{i=1}^{N}(D_i - \bar{D})^2}\)	与方差意义一致，单位与测量距离一致，更直观	方差的平方根
峰值-峰值（Peak-to-Peak）	D_{p-p} = D_{max} - D_{min}	反映数据的最大波动范围	数据中的最大值减去最小值
变异系数（Coefficient of Variation）	CV = \frac{\sigma}{\bar{D}} \times 100\%	反映数据的相对波动程度，不受测量单位影响	标准差与均值的比值，用百分比表示

2.3 实验数据波动特性分析

根据上述实验采集的直射场景和遮挡场景下的距离数据，计算各统计指标，结果如下表所示：

实验场景	均值（m）	方差（m²）	标准差（m）	峰值-峰值（m）	变异系数（%）
直射场景	4.98	0.0012	0.0346	0.21	0.69
遮挡场景	5.02	0.0156	0.1249	1.05	2.49

从实验结果可以看出：

1. 遮挡场景下的距离数据波动远大于直射场景，其标准差是直射场景的3.6倍，变异系数是直射场景的3.6倍，说明多径效应和遮挡是导致距离数据波动的主要原因。

2. 直射场景下，距离数据的均值接近真实距离（5m），而遮挡场景下均值略有偏差，说明遮挡不仅会导致波动增大，还可能引入系统误差。

3. 两种场景下的峰值-峰值差异显著，遮挡场景下最大波动范围达到1.05m，严重影响定位精度，因此必须对距离数据进行波动抑制处理。

三、Allan方差数据统计分析——波动溯源与量化

Allan方差（Allan Variance, AV）是由David W. Allan于1966年提出的一种用于分析随机过程的统计方法，最初主要用于原子钟的频率稳定性分析。由于Allan方差对不同类型的随机误差具有良好的分辨能力，近年来被广泛应用于传感器数据波动分析、定位数据处理等领域。本节将详细讲解Allan方差的基本原理、在UWB距离数据波动分析中的应用、软件算法实现及结果分析。

3.1 Allan方差基本原理

3.1.1 定义与数学表达式

对于平稳随机过程的离散时间序列\(\{x_i\}\)（\(i=1,2,...,N\)），其Allan方差的定义为：在采样时间间隔为\(\tau_0\)的情况下，取不同的平均时间\(\tau = m\tau_0\)（\(m\)为平均次数，\(m=1,2,...,M\)，\(M \leq N/2\)），计算相邻两个平均数据的差值的平方的一半的均值，数学表达式为：

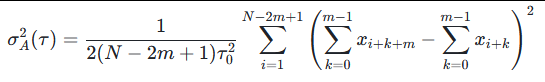
简化表达式（当数据量足够大时，\(N-2m+1 \approx N\)）：