无人机中的数学应用第四章：信号传输 —— 数学保障通信稳定性-优快云博客

本文链接：https://blog.youkuaiyun.com/bother3000/article/details/149698146

4.0 数字信号通信：从原理到历史的演进
4.0.1 通信的本质：信息如何 “跨越空间”？
4.0.2 模拟信号与数字信号：通信世界的 “两种语言”
4.0.3 数字信号通信的核心原理：编码、调制与解调
4.0.4 通信技术发展简史：从烽火台到 5G 无人机
4.0.5 无人机通信的特殊性：为何数学是 “稳定器”？

5.1 菲涅尔区与通视性分析
5.1.1 电磁波的 “绕弯” 能力：绕射现象的直观理解
5.1.2 菲涅尔区：电磁波的 “隐形安全通道”
5.1.3 第一菲涅尔区半径：计算公式与物理意义
5.1.4 通视性判断：如何用数学确定信号 “是否通畅”？
5.1.5 无人机通信中的菲涅尔区应用：避开遮挡的实战技巧

5.2 无人机通信链路预算：数学计算信号 “够不够强”
5.2.1 链路预算的 “收支平衡”：从发射到接收的能量账
5.2.2 自由空间损耗：距离如何 “削弱” 信号？
5.2.3 地形附加损耗：不同环境对信号的 “额外消耗”
5.2.4 链路预算的完整计算：无人机通信的 “可行性报告”
5.2.5 抗衰落设计：数学如何帮信号 “对抗衰减”？

5.3 不同地形下的信号优化策略：用数学 “定制” 通信方案
5.3.1 开阔地通信：平原地区的信号 “畅行无阻”
5.3.2 山地通信：如何让信号 “翻山越岭”？
5.3.3 城市通信：高楼间的信号 “穿梭术”
5.3.4 雨林与海洋：特殊环境的信号 “生存法则”
5.3.5 多地形自适应通信：无人机如何 “智能切换” 模式？

4.0 数字信号通信：从原理到历史的演进

4.0.1 通信的本质：信息如何 “跨越空间”？

通信的本质是信息的传递—— 无论是无人机与地面站的指令交互，还是手机通话，核心都是将 “想法”“数据” 转化为可传输的信号，通过介质（如空气、电缆）送到目的地后再还原。

比如，无人机拍摄的高清图像包含上亿个像素，这些信息无法直接 “扔” 向地面，必须先转化为电信号或电磁波，就像写信时要把想法转化为文字。数学在这里的作用，是让这个 “转化 - 传输 - 还原” 的过程更高效、更可靠。

通信系统的基本组成（用无人机举例）：

信源：无人机的摄像头、传感器（产生图像、海拔等信息）
发送设备：无人机的信号发射器（将信息转化为电磁波）
信道：空气（电磁波传播的 “通道”，会受地形、天气影响）
接收设备：地面站的天线（捕捉电磁波并转化为电信号）
信宿：地面站的显示屏、处理器（还原出图像、数据）

这个过程中，每一步都依赖数学：比如信号的编码方式（用二进制 0 和 1 表示信息）、电磁波的传播路径计算（确保信号能到达）、噪声的过滤（用算法提取有效信号）。

4.0.2 模拟信号与数字信号：通信世界的 “两种语言”

通信信号分为模拟信号和数字信号，二者的区别就像 “手写体” 与 “印刷体”：

对比维度	模拟信号	数字信号	无人机中的应用场景
表现形式	连续变化的波形（如声波、正弦波）	离散的 “0” 和 “1” 脉冲（如方波）	模拟：早期无人机的遥控指令（简单）
抗干扰能力	弱（噪声会改变波形，难以还原）	强（0 和 1 只有两种状态，易区分）	数字：现代无人机的高清图传、加密数据
传输效率	低（无法压缩，占用带宽大）	高（可压缩、编码，节省带宽）	数字：长距离侦察任务（节省能量）
数学基础	连续函数（如正弦函数 y=A sin (ωt)）	离散数学（二进制、矩阵运算）	数字：需要复杂算法的场景

举例：

模拟信号：老式收音机接收的广播，信号受干扰会有杂音，就像手写体被弄脏后难以辨认。
数字信号：手机发送的微信消息，即使信号弱，也能通过纠错码还原完整内容，就像印刷体模糊后仍能识别。

无人机为何多用数字信号？因为无人机需要传输高清图像、精确坐标等复杂信息，且常处于复杂环境（如山区、城市），数字信号的抗干扰能力和高效性更适合。

4.0.3 数字信号通信的核心原理：编码、调制与解调

数字信号从产生到被接收，需经过编码→调制→传输→解调→解码五个步骤，每个步骤都离不开数学：

编码：将信息转化为二进制（0 和 1）
比如无人机拍摄的一个像素点亮度（0-255），可编码为 8 位二进制（如亮度 128→10000000）。
数学工具：信息论（香农定理），确保用最少的 0 和 1 表示最多的信息。
调制：将二进制信号 “加载” 到电磁波上
电磁波有三个参数：振幅（强度）、频率（快慢）、相位（起始位置）。调制就是通过改变这三个参数来 “携带” 0 和 1：
- 调幅（AM）：用振幅高低表示 0 和 1（高振幅 = 1，低振幅 = 0）
- 调频（FM）：用频率快慢表示 0 和 1（高频 = 1，低频 = 0）
- 调相（PM）：用相位变化表示 0 和 1（相位 0°=0，180°=1）
  数学工具：三角函数（如调幅信号 y=A (1+k・s (t)) sin (ωt)，s (t) 为 0/1 信号）。
传输：电磁波在空间中传播
传播过程中会衰减（能量减少）、受干扰（如其他电磁波的影响）。
数学工具：波动方程（描述电磁波传播）、概率论（分析干扰的随机性）。
解调：从电磁波中 “提取” 二进制信号
接收端通过电路 “反向操作” 调制，比如调幅信号通过检测振幅高低还原 0 和 1。
数学工具：傅里叶变换（分离不同频率的信号）。
解码：将二进制还原为原始信息
比如 8 位二进制 10000000 还原为亮度 128，再组合成图像。
数学工具：纠错码（如汉明码，通过额外的 0 和 1 修正错误）。

总结：数字信号通信就像 “打包快递”—— 编码是把物品装箱（二进制），调制是给箱子贴地址（加载到电磁波），传输是运输过程（会遇到路况问题），解调和解码是拆箱取物（还原信息）。数学则是 “打包规则”“路线规划” 和 “防损坏措施”。

4.0.4 通信技术发展简史：从烽火台到 5G 无人机

通信技术的发展史，本质是 “用数学解决更远、更快、更可靠传输” 的历史。以下是关键阶段：

时间	关键技术	数学突破	无人机相关应用
古代	烽火台、信鸽	几何（视线距离计算）	无（未发明）
1837 年	莫尔斯电码（有线电报）	离散符号（点和划表示字母）	无
1895 年	无线电报（马可尼）	电磁学方程（麦克斯韦方程组）	奠定无人机无线通信基础
1940 年代	调频（FM）技术	傅里叶变换（频率分析）	早期无人机遥控（简单指令）
1960 年代	数字通信（二进制）	信息论（香农定理，1948 年提出）	军用无人机开始传输数字坐标
1980 年代	蜂窝移动通信（2G）	编码理论（纠错码）	民用无人机短距离遥控
2000 年代	4G 技术	正交频分复用（OFDM，矩阵运算）	无人机高清图传（1080P）
2020 年代	5G 与卫星通信	机器学习（信号预测与优化）	无人机编队通信、超视距控制

关键突破解析：

麦克斯韦方程组（1864 年）：用数学公式预言了电磁波的存在，为无线电通信奠定基础。没有这组方程，就没有无人机的无线遥控。
香农定理（1948 年）：指出 “在一定带宽和噪声下，通信速率有上限”，公式为 C=B log₂(1+S/N)（C 为速率，B 为带宽，S/N 为信噪比）。无人机设计时，需用此定理计算 “最多能传输多少数据”。
OFDM 技术（1990 年代成熟）：将信道分成多个子信道并行传输，用傅里叶变换处理频率，大幅提升速率。现代无人机图传（如 5.8GHz 图传）普遍采用。

4.0.5 无人机通信的特殊性：为何数学是 “稳定器”？

无人机通信与手机、广播等通信不同，有三个核心挑战，而数学是解决这些挑战的关键：

移动性强：无人机快速飞行时，与地面站的距离、角度不断变化，信号强度波动大。
数学解决方案：用多普勒效应公式（Δf = (v/c) f₀ cosθ，v 为速度，c 为光速，θ 为夹角）计算频率偏移，提前修正接收参数。
环境复杂：无人机常飞行在山区、城市等地形复杂区域，信号易被遮挡。
数学解决方案：菲涅尔区计算（判断遮挡程度）、地形损耗模型（预测信号衰减）。
能耗受限：无人机电池容量有限，发射功率不能太大（否则耗电快）。
数学解决方案：链路预算优化（用最少功率满足通信需求）、压缩算法（减少传输数据量）。

举例：
一架侦察无人机在山区飞行，需要将 1080P 图像（约 5MB / 帧）传回 20 公里外的地面站。若直接传输，需大功率发射器（耗电快）且易受地形遮挡。通过数学优化：

压缩算法（如 H.265）将图像压缩至 1MB / 帧（节省 80% 带宽）；
菲涅尔区计算避开山峰遮挡，选择最佳飞行高度；
链路预算计算确定发射功率（如 1W），确保接收端能识别信号。

5.1 菲涅尔区与通视性分析

5.1.1 电磁波的 “绕弯” 能力：绕射现象的直观理解

电磁波（包括无人机通信的无线电波）并非严格 “走直线”，遇到障碍物时会像水流绕石头一样 “绕弯”—— 这种现象称为绕射。

生活中的绕射例子：

隔墙听声音：声波绕射（低频声波绕射能力强，所以能听到邻居的低音）。
无线电信号绕山：中波广播（波长几百米）能绕过大山，而电视信号（波长几米）易被遮挡。

绕射能力与波长密切相关：波长越长（频率越低），绕射能力越强。比如：

长波（波长 1km）：能绕过大山、高楼，适合远距离通信（如潜艇通信）。
毫米波（波长 1mm）：绕射能力弱，几乎沿直线传播，适合短距离高清通信（如无人机近距离图传）。

无人机通信常用频段及绕射能力：

频段	波长	绕射能力	无人机应用场景	缺点
1.2GHz	25cm	较强	长距离侦察（10km 以上）	带宽窄，图像分辨率低
2.4GHz	12.5cm	中等	中距离控制（1-5km）	易受 WiFi 干扰
5.8GHz	5.2cm	较弱	近距离高清图传（1km 内）	绕射差，遮挡后信号易断

5.1.2 菲涅尔区：电磁波的 “隐形安全通道”

菲涅尔区是围绕 “直射路径”（发射端到接收端的直线）的一系列同心椭球区域，就像多层洋葱环绕中轴线。电磁波的能量主要通过这些区域传播，尤其是第一菲涅尔区（最内层），包含约 90% 的能量。

形象理解：
把电磁波想象成 “水流”，直射路径是 “主河道”，菲涅尔区是 “河道两侧的浅滩”。若浅滩被完全堵塞（障碍物侵入第一菲涅尔区），水流（信号）就会大幅减少；若只堵塞一部分，水流仍能绕过。

菲涅尔区的特点：

离发射端和接收端越近，菲涅尔区半径越小；中间位置半径最大。
波长越长，菲涅尔区半径越大（长波的 “安全通道” 更宽）。

为什么菲涅尔区重要？
无人机通信中，即使发射端和接收端 “视线可见”（无直接遮挡），若障碍物（如树木、电线杆）侵入第一菲涅尔区，信号仍会严重衰减。比如：

一架无人机在 500 米高度飞行，地面站在 2 公里外，中间有一棵 20 米高的树。若树的顶端进入第一菲涅尔区，图传可能出现卡顿。

5.1.3 第一菲涅尔区半径：计算公式与物理意义

第一菲涅尔区的最大半径（中间位置）计算公式为：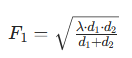

其中：

F1：第一菲涅尔区半径（单位：米）
λ：电磁波波长（单位：米，λ = 光速 / 频率，如 5.8GHz 的 λ≈0.052 米）
d1：障碍物到发射端的距离（单位：米）
d2：障碍物到接收端的距离（单位：米）

计算示例：
无人机（发射端）与地面站（接收端）相距 2000 米，中间有一障碍物（距无人机 1000 米，距地面站 1000 米），使用 5.8GHz 频段（λ=0.052 米）：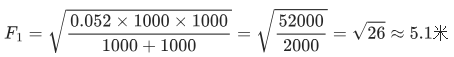

即障碍物顶端到直射路径的垂直距离需小于 5.1 米，才不会严重影响信号。

不同频段的菲涅尔区半径对比（距离 2000 米，中间障碍物）：

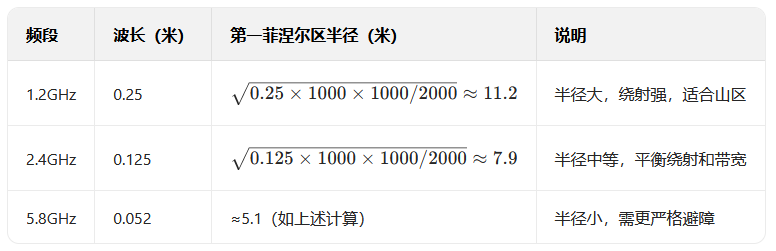
5.1.4 通视性判断：如何用数学确定信号 “是否通畅”？

通视性并非 “看得见就通畅”，而是指 “第一菲涅尔区是否被严重遮挡”。判断标准：

若障碍物顶端到直射路径的垂直距离 h≤0.6×F1：信号通畅（绕射足够）。
若 h>0.6×F1：信号衰减严重（视为 “不通视”）。

0.6 倍的由来：
工程实践发现，当障碍物侵入第一菲涅尔区的 40% 以内（即保留 60% 以上），绕射损耗小于 1dB（几乎无影响）；超过 40%，损耗急剧增加（如侵入 50% 时损耗达 6dB，信号强度减半）。

步骤：判断无人机与地面站的通视性

测量：无人机高度 H1、地面站高度 H2、障碍物高度 H3、障碍物到无人机水平距离 d1、到地面站水平距离 d2。
计算直射路径在障碍物处的高度 H0：
直射路径是直线，高度随距离线性变化：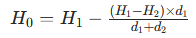
计算障碍物相对直射路径的高度差 h：h=H3−H0
（若 h<0，说明障碍物在直射路径下方，无遮挡）
计算第一菲涅尔区半径 F1（用之前的公式）。
比较 h 与 0.6×F1：
- h≤0.6×F1：通视良好
- h>0.6×F1：信号受遮挡

实例：
无人机在 100 米高度（H1=100），地面站在 10 米高度（H2=10），中间有一山丘：

d1=1000米，d2=1000米，山丘高度 H3=80米，使用 2.4GHz（λ=0.125 米）。

步骤 1：计算

步骤 2：计算

步骤 3：计算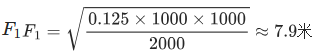

步骤 4：

5.1.5 无人机通信中的菲涅尔区应用：避开遮挡的实战技巧

无人机飞行中，需实时计算菲涅尔区，调整高度或路径以避免信号遮挡。以下是具体方法：

预规划路径时避开高障碍物
在地图上标记山峰、高楼等障碍物，计算其是否侵入第一菲涅尔区。若侵入，规划绕行路线或提高飞行高度。

例：某山区任务，无人机需从 A 到 B（2 公里），中间有一 30 米高山峰。计算发现山峰侵入第一菲涅尔区，于是将路径偏移 50 米，绕过山峰。
动态调整高度
飞行中用传感器（如 GPS、气压计）实时获取自身和障碍物高度，计算 h 并与 0.6×F1 比较，若 h 过大，自动升高高度。

公式：需升高的最小高度 ΔH=h−0.6×F1
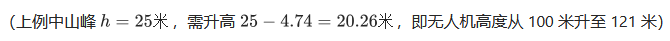
选择合适频段（建议同学们检查回看第一章内容，航迹规划）
复杂地形优先用长波（如 1.2GHz），其更大的菲涅尔区半径能容忍更多遮挡。例如：
- 5.8GHz 在山区可能需要升高 50 米才能避开遮挡；
- 1.2GHz 可能只需升高 20 米（因 F1 更大，0.6×F₁也更大）。

5.2 无人机通信链路预算：数学计算信号 “够不够强”

5.2.1 链路预算的 “收支平衡”：从发射到接收的能量账

链路预算是计算 “信号从发射到接收的能量变化”，判断接收端能否 “读懂” 信号。核心公式：

发射功率（Pₜ）：无人机发射器输出的功率（单位：dBm，1dBm=1 毫瓦，30dBm=1 瓦）。
总损耗（Lₜₒₜₐₗ）：信号传输中的各种衰减（自由空间损耗、地形损耗等）。
天线增益（Gₜ + Gᵣ）：发射天线和接收天线对信号的放大作用（单位：dBi，全向天线约 2dBi，定向天线可达 10dBi 以上）。
接收灵敏度（Pᵣₘᵢₙ）：接收端能识别的最小功率（如 - 100dBm，值越小接收能力越强）。

链路预算的目标：接收功率 ≥ 接收灵敏度（即 Pr≥Prmin）。

5.2.2 自由空间损耗：距离如何 “削弱” 信号？

即使在无遮挡的理想环境（如空旷平原），信号也会因 “扩散” 而衰减 —— 这称为自由空间损耗（FSL），与距离的平方成正比：

举例：
无人机用 5.8GHz（5800MHz）在 1 公里处通信：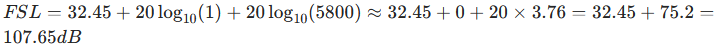

距离对损耗的影响（5.8GHz）：

距离（公里）	自由空间损耗（dB）	信号衰减倍数（相对于 1 公里）
1	107.65	1
2	113.67（+6dB）	4（损耗翻倍，信号强 1/4）
5	123.65（+16dB）	25
10	130（+22.35dB）	100

结论：距离每增加一倍，自由空间损耗增加约 6dB（信号强度变为 1/4）。因此，无人机远距离通信需大功率发射器或高增益天线。

5.2.3 地形附加损耗：不同环境对信号的 “额外消耗”

除自由空间损耗，地形会带来额外损耗（Lₜₑᵣᵣₐᵢₙ）。以下是常见地形的附加损耗：

地形类型	附加损耗（dB）	原因分析	无人机应对策略
开阔地	0-5	几乎无遮挡，仅少量地面反射	用全向天线，功率可降低
郊区（低矮建筑）	10-20	房屋、树木遮挡，反射较多	提高飞行高度，避开密集建筑群
城市（高楼）	20-35	高楼遮挡严重，多径效应（信号反射后相互干扰）	用定向天线（对准地面站），缩短通信距离
丘陵	15-25	起伏地形部分遮挡，绕射损耗	选择山顶作为中继点
山地（陡峭）	30-40	山峰遮挡，需绕射传播	改用长波（1.2GHz），增加发射功率
雨林	15-25	树叶吸收信号（尤其高频）	降低飞行高度，贴近树梢飞行

多径效应：
城市中，信号除直射路径外，还会经高楼反射形成 “多条路径” 到达接收端，不同路径的信号可能相互抵消（如相位相反），导致接收功率忽强忽弱（“快衰落”）。数学解决方案：用分集接收（多天线接收不同路径信号），通过矩阵运算选择最强信号。

5.2.4 链路预算的完整计算：无人机通信的 “可行性报告”

步骤：计算某城市环境下的链路预算
无人机参数：发射功率 20dBm（100 毫瓦），发射天线增益 2dBi，接收天线增益 5dBi，接收灵敏度 - 100dBm。
任务：城市中通信，距离 1 公里，5.8GHz 频段。

计算自由空间损耗（FSL）：

加地形附加损耗（城市取 30dB）：

计算接收功率：

对比接收灵敏度：
-110.65 dBm < -100 dBm（接收功率低于灵敏度）→ 通信不可行。

改进方案：

换用定向天线（增益 10dBi）：接收功率 = 20+10+5-137.65 = -102.65 dBm（仍略低）。
再提高发射功率至 27dBm（500 毫瓦）：接收功率 = 27+10+5-137.65 = -95.65 dBm ≥ -100 dBm → 可行。

5.2.5 抗衰落设计：数学如何帮信号 “对抗衰减”

即使链路预算达标，信号仍可能因突发干扰（如阵风导致无人机晃动、突发电磁干扰）衰减，需用数学方法增强抗干扰能力：

功率控制：
实时监测接收功率，用 PID 算法调整发射功率：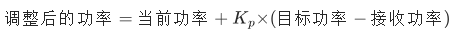

（K_p 为比例系数，目标功率通常比灵敏度高 10dB，留有余地）

纠错编码：
在数据中加入冗余信息（如每 8 位数据加 4 位校验位），接收端用数学算法（如海明码、Turbo 码）纠正错误。
例：Turbo 码在信噪比为 1dB 时，误码率可低至 10⁻⁶（几乎无错误）。

跳频技术：
信号在多个频率间快速切换（如每秒 1000 次），避开干扰频率。数学上用伪随机序列（如 m 序列）生成跳频图案，确保收发端同步。

5.3 不同地形下的信号优化策略：用数学 “定制” 通信方案

5.3.1 开阔地通信：平原地区的信号 “畅行无阻”

开阔地（如草原、沙漠）是最理想的通信环境，损耗主要来自自由空间，优化策略聚焦 “高效传输”：

优化目标	数学方法	具体措施
最大化传输速率	香农定理（C=B log₂(1+S/N)）	用高频段（5.8GHz）增加带宽（B），降低功率节省能耗
延长通信距离	自由空间损耗公式（L∝d²）	用定向天线（增益 10dBi），补偿距离损耗
抗干扰	信噪比（S/N）最大化	跳频技术避开干扰，纠错编码（如 LDPC 码）

例：草原侦察任务（10 公里）

频段：2.4GHz（平衡速率和绕射）
链路预算：发射功率 25dBm（316 毫瓦）+ 定向天线 10dBi → 接收功率 - 90dBm（高于灵敏度 - 100dBm）
数据速率：2Mbps（足够传输实时视频）

5.3.2 山地通信：如何让信号 “翻山越岭”

山地通信的核心是 “克服遮挡”，需结合菲涅尔区计算和频段选择：

路径规划：
用数字高程模型（DEM）生成地形剖面，计算各点菲涅尔区，选择 “菲涅尔区被遮挡最少” 的路径。数学工具：地形梯度分析（寻找坡度平缓的路线）。
中继策略：
在山顶部署中继无人机（或地面站），形成 “多跳通信”。中继点选择需满足：

与前一站通视（菲涅尔区无遮挡）

覆盖尽可能多的下一站

数学模型：用图论（最小生成树）选择最优中继点，使总损耗最小。

频段选择：
对比不同频段的绕射能力和损耗：

频段	10 公里损耗（dB）	需发射功率（dBm）	优势
1.2GHz	自由空间 70 + 山地 30 = 100	20（100 毫瓦）	绕射强，适合多山区域
2.4GHz	自由空间 76 + 山地 30 = 106	26（400 毫瓦）	速率较高，平衡性能
5.8GHz	自由空间 88 + 山地 30 = 118	38（6.3 瓦）	速率高，但需大功率，适合短距离

结论：优先用 1.2GHz，若需高清图传，用 2.4GHz 并增加中继。

5.3.3 城市通信：高楼间的信号 “穿梭术”

城市通信的最大挑战是多径效应和遮挡，优化策略聚焦 “避开障碍、增强抗干扰”：

波束成形技术：
用多天线阵列（如 4 根天线），通过矩阵运算控制每个天线的相位，使信号在目标方向叠加增强，在干扰方向抵消。数学工具：MIMO（多输入多输出）系统，信道矩阵奇异值分解。
高度优化：
城市中，信号强度随高度先增后减（低空受遮挡，高空多径效应强），存在 “最佳高度”。通过多次测量拟合函数：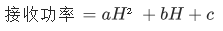

求导得最佳高度 H=−b/(2a)（通常在 50-100 米）。

3.中继网络：
在高楼顶部部署固定中继点，形成 “蜂窝网络”，无人机在不同区域自动切换中继。数学模型：用马尔可夫链预测无人机移动轨迹，提前切换中继。

5.3.4 雨林与海洋：特殊环境的信号 “生存法则”

雨林：树叶对电磁波（尤其高频）吸收强，优化策略：
- 用长波（1.2GHz）减少吸收损耗；
- 低空飞行（50 米以下），利用树干间的空隙传播；
- 缩短通信距离（如每 2 公里设一中继）。
海洋：海面反射导致 “镜像干扰”（直射信号与海面反射信号抵消），优化策略：
- 调整天线角度，使反射信号与直射信号相位相同（ constructive interference）；
- 用圆极化天线（如右旋圆极化），减少反射信号干扰（反射后极化方向反转）。

5.3.5 多地形自适应通信：无人机如何 “智能切换” 模式

先进无人机可通过传感器（GPS、陀螺仪、摄像头）识别地形，自动切换通信参数，实现 “一处一策”：

地形识别	切换参数	数学决策依据
从开阔地进入城市	频段从 5.8GHz→2.4GHz，开启跳频	检测到多径衰落（方差 > 10dB），触发切换
进入山地	发射功率增加 5dB，天线切换为全向	菲涅尔区遮挡率 > 40%，自由空间损耗突增
进入雨林	降低数据速率（从 2Mbps→500kbps）	接收信号强度 < -90dBm，通过降低速率提高信噪比

自适应算法：
用强化学习训练无人机，将 “地形特征→通信参数→信号质量” 作为训练数据，通过 Q-learning 算法找到最优策略。例如：