PMSM学习（4）——控制方式总结

同步电机主要控制方法（含SynRM与PMSM）

一、矢量控制

1.最大转矩/电流比控制——MTPA

这是在定子电流最优控制问题在恒转矩控制下提出的控制方法。
已知PMSM转矩方程为$T_e=p[{\Psi }_f{i}_q+(L_d-L_q)i_d{i}_q]$，可以转换成将电感值进行标幺值变换可得转矩方程形式为$T_e=p[e_0{i}_s\sin \beta +\frac{1}{2}(1-\rho )x_d{i}_s^2\sin 2\beta ]，\beta$为定子电流矢量角。
对上式求极小值，即$\frac{\partial T_e}{\partial i_s}=0，$可得$\beta =\frac{\pi }{2}+\arcsin [\frac{-e_0+\sqrt{e_0^2+8(\rho -1{)}^2{x}_d^2{i}_s^2}}{4(\rho -1)x_d{i}_s}]。$
由于受到电流极限圆的限制，即$i_d^2+i_q^2⩽i_{smax}^2$，所以在电流极限圆内的最大转矩/电流比轨迹部分便是矢量控制过程中的变化。
如图所示

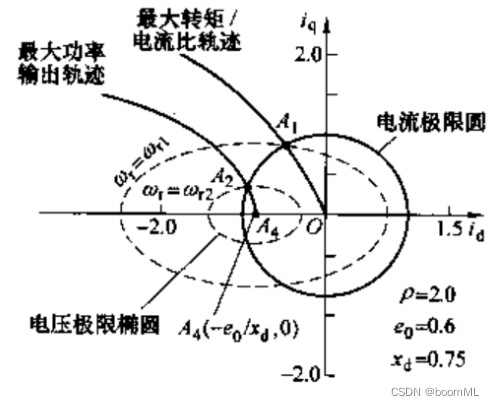
其中的最大转矩/电流比轨迹的生成过程

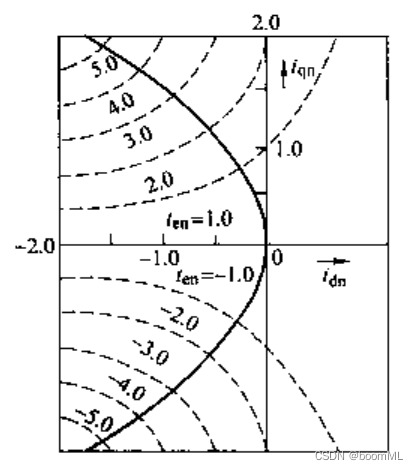
对于虚线部分为定子电流矢量轨迹，推导过程如下，
$T_e=p[{\Psi }_f{i}_q+(L_d-L_q)i_d{i}_q]，$标幺值形式可推导为$\{\begin{array}{l}{T}_{en}=i_{qn}(1-i_{dn});\\ i_b=\frac{{\Psi }_f}{L_q-L_d};\\ i_{qn}=\frac{i_q}{i_b};\\ i_{dn}=\frac{i_d}{i_b};\\ T_{eb}=p{\Psi }_f{i}_b;\end{array}，$求极值可得
$\{\begin{array}{l}{T}_{en}=\sqrt{i_{dn}(i_{dn}-1{)}^3}\\ T_{en}=\frac{i_{qn}}{2}(1+\sqrt{1+4i_{qn}^2})\end{array}，$可得虚线部分，二象限为驱动部分，三象限为制动部分。
为了得到最大转矩/电流比，即$\frac{T_e}{i_s}，$需要确保在恒转矩时定子电流最小，所以在虚线部分取定子电流$i_s^2=i_d^2+i_q^2$最小的点，可以连成实线部分——最大转矩/电流比轨迹，同理最大功率输出控制。

MTPA是效率最高的一种控制方式

2.最大功率输出控制

$T_e=p[e_0{i}_s\sin \beta +\frac{1}{2}(1-\rho )x_d{i}_s^2\sin 2\beta ]，P_e=\frac{{\omega }_r{T}_e}{p}={\omega }_r[e_0{i}_s\sin \beta +\frac{1}{2}(1-\rho )x_d{i}_s^2\sin 2\beta ]$
在电压极限椭圆和电流极限圆的限制下，电压极限椭圆为$(e_0+x_d{i}_d{)}^2+(\rho x_q{i}_q{)}^2=(\frac{|u_S|}{{\omega }_r}{)}^2$得到相应工作点。

3.最大功率因数控制——MPFC

由于使用高功率因数，可以实现低成本高效率控制。功率因数角为定子电压与定子电流的夹角，$\cos \psi =\frac{L_d-L_q}{\sqrt{\frac{L_d^2}{\sin \beta }}+\frac{L_q^2}{\cos \beta }}，$最终可以转换成定子电流矢量角$\beta ={\tan }^{-1}\sqrt{\xi },\xi =\frac{L_d}{L_q},\xi$为电机凸极率。
关注理想最高功率因数$P{F}_{max}=\frac{\xi -1}{\xi +1}。$

4.最大转矩变化率控制——MRCTC

关注动态转矩，使得电机电磁转矩快速响应外界负载的变化。
$\partial T_e/\partial \beta =0\to \beta ={\tan }^{-1}\xi ,\xi =\frac{L_d}{L_q}。$

二、弱磁控制

弱磁控制是为了解决电流调节器饱和限制了速度范围，当电机运行到电压极限椭圆处，电流调节器已处于饱和状态，即控制系统丧失了对定子电流的控制能力。
所以应减小$i_q$增大$i_d$使$i_s$向左偏向，从而使$|u_s|$减小，使进入电压极限椭圆内而脱离饱和状态，从而恢复定子电流的控制功能，最终使得转子速度范围得以扩展。

补充

反向$i_d$有去磁作用，即增大$i_d$便是增强弱磁功能。

三、直接转矩控制

对在定子坐标系下的磁链转矩公式，直接对定子磁通和转矩进行控制（一般是滞环比较控制），且直接转矩控制不包含电流环，不需要进行复杂的坐标变换，对电机参数依赖较小。