一、矢量控制基础
转矩方程: T e = p Ψ s × i s T_e=p\varPsi_s\times i_s Te=pΨs×is
二、基于转子磁场定向的矢量控制
1.转子磁场定向
转子磁场与电驱磁场相互作用产生转矩,即转矩方程可等为
T
e
=
p
1
L
s
Ψ
f
×
Ψ
s
,
T_e=p\tfrac{1}{Ls}\varPsi_f\times\varPsi_s,
Te=pLs1Ψf×Ψs,可以通过坐标变换将矢量变换到dq轴上(与转子同步旋转的运动轴),并使d轴与
Ψ
f
\varPsi_f
Ψf方向一致,或者说dq轴系沿着转子磁场定向的。
通过坐标变换将复杂的PMSM的模型等效成直流电机模型,且在dq轴下可以解耦,可以实现弱磁和转矩的分开控制。
2.坐标变换
2.1 Clark变换:从A-B-C三相静止坐标轴变换到 α β \alpha\beta αβ两相静止轴系

{
i
α
=
i
A
+
i
B
cos
(
12
0
∘
)
+
i
C
cos
(
−
12
0
∘
)
i
β
=
i
B
cos
(
3
0
∘
)
−
i
C
cos
(
3
0
∘
)
i
0
=
0
\begin{cases} i_\alpha=i_A+i_B\cos(120^\circ)+i_C\cos(-120^\circ) \\i_\beta=i_B\cos(30^\circ)-i_C\cos(30^\circ) \\i_0=0\end{cases}
⎩
⎨
⎧iα=iA+iBcos(120∘)+iCcos(−120∘)iβ=iBcos(30∘)−iCcos(30∘)i0=0
[
i
α
i
β
i
0
]
=
[
1
−
1
2
−
1
2
0
1
2
1
2
2
2
2
2
2
2
]
⋅
[
i
A
i
B
i
C
]
\begin{bmatrix}i_\alpha\\i_\beta\\i_0\end{bmatrix}=\begin{bmatrix}1&-\tfrac{1}{2}&-\tfrac{1}{2}\\0&\tfrac{1}{2}&\tfrac{1}{2}\\\tfrac{\sqrt2}{2}&\tfrac{\sqrt2}{2}&\tfrac{\sqrt2}{2}\end{bmatrix}\cdotp\begin{bmatrix}i_A\\i_B\\i_C\end{bmatrix}
⎣
⎡iαiβi0⎦
⎤=⎣
⎡1022−212122−212122⎦
⎤⋅⎣
⎡iAiBiC⎦
⎤
由上可知
T
3
s
/
2
s
=
[
1
−
1
2
−
1
2
0
1
2
1
2
2
2
2
2
2
2
]
T_{3s/2s}=\begin{bmatrix}1&-\tfrac{1}{2}&-\tfrac{1}{2}\\0&\tfrac{1}{2}&\tfrac{1}{2}\\\tfrac{\sqrt2}{2}&\tfrac{\sqrt2}{2}&\tfrac{\sqrt2}{2}\end{bmatrix}
T3s/2s=⎣
⎡1022−212122−212122⎦
⎤
2.2 Park变换:从 α β \alpha\beta αβ两相静止轴系变换到dq两相同步旋转轴系
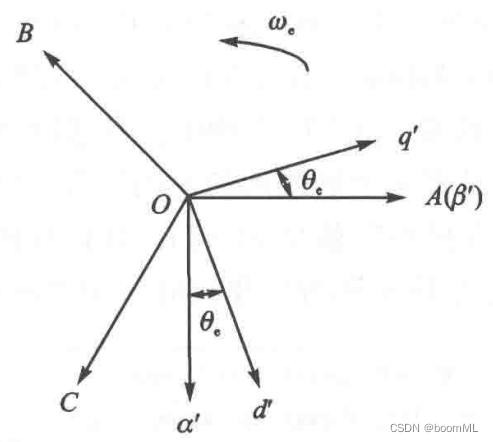
{
i
d
=
i
α
cos
θ
e
+
i
β
sin
θ
e
i
q
=
−
i
α
sin
θ
e
+
i
β
cos
θ
e
\begin{cases} i_d=i_\alpha\cos\theta_e+i_\beta\sin\theta_e\\i_q=-i_\alpha\sin\theta_e+i_\beta\cos\theta_e \end{cases}
{id=iαcosθe+iβsinθeiq=−iαsinθe+iβcosθe
[
i
α
i
β
]
=
[
cos
θ
e
sin
θ
e
−
sin
θ
e
cos
θ
e
]
⋅
[
i
α
i
β
]
\begin{bmatrix}i_\alpha\\i_\beta\end{bmatrix}=\begin{bmatrix}\cos\theta_e&\sin\theta_e\\-\sin\theta_e&\cos\theta_e\end{bmatrix}\cdotp\begin{bmatrix}i_\alpha\\i_\beta\end{bmatrix}
[iαiβ]=[cosθe−sinθesinθecosθe]⋅[iαiβ]
由上可知
T
2
s
/
2
r
=
[
cos
θ
e
sin
θ
e
−
sin
θ
e
cos
θ
e
]
T_{2s/2r}=\begin{bmatrix}\cos\theta_e&\sin\theta_e\\-\sin\theta_e&\cos\theta_e\end{bmatrix}
T2s/2r=[cosθe−sinθesinθecosθe]
3.磁链方程与电压方程
表贴式和内插式PMSM的转子磁场定向(dq轴)的磁链方程、电压方程和转矩方程
4.面装式三相永磁同步电动机的矢量控制及控制系统
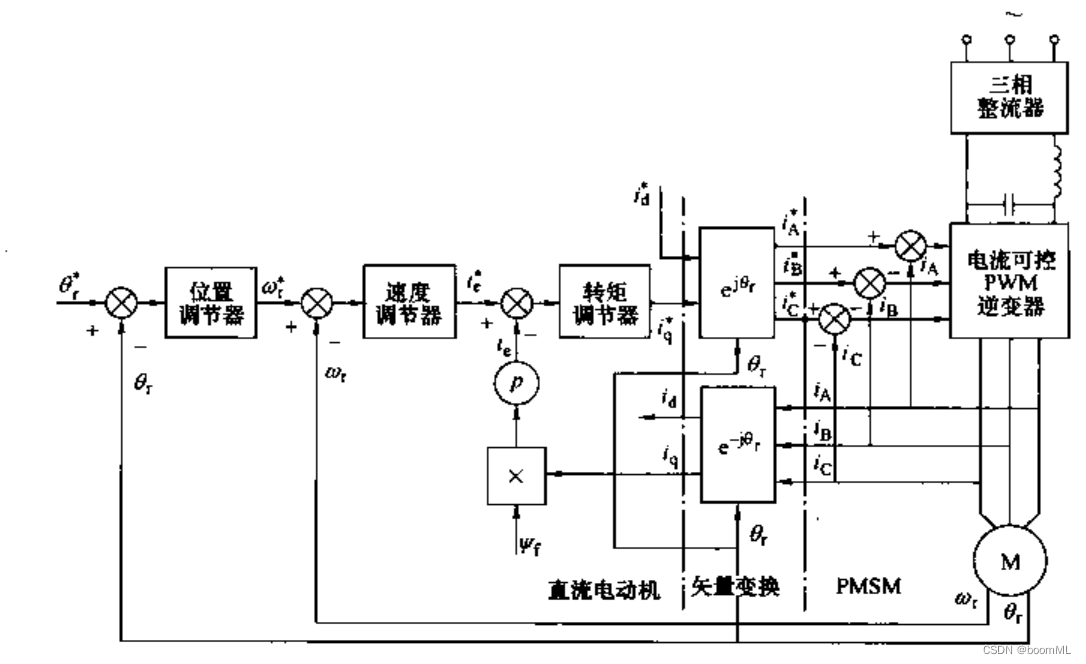
转矩方程可以简化为 T e = p Ψ f i q T_e=p\varPsi_fi_q Te=pΨfiq,此时 i q i_q iq为转矩电流,可知最佳控制为 i d = 0 i_d=0 id=0,控制 i q i_q iq即相当于控制电枢电流,可以获得与他励直流电动机同样的转矩控制效果,弱磁控制则由 i d i_d id控制。
系统框图可为
5.插入式三相永磁同步电动机的矢量控制及控制系统
转矩方程可以简化为
T
e
=
p
(
Ψ
f
i
q
+
(
L
d
−
L
q
)
i
d
i
q
)
T_e=p(\varPsi_fi_q+(L_d-L_q)i_di_q)
Te=p(Ψfiq+(Ld−Lq)idiq),最佳控制需要跟随最大转矩/电流比。
将上述转矩方程标幺值化可得
T
e
n
=
i
q
n
(
1
−
i
d
n
)
T_{en}=i_{qn}(1-i_{dn})
Ten=iqn(1−idn),基值为
T
e
b
=
p
Ψ
f
i
b
,
i
b
=
Ψ
f
L
q
−
L
d
T_{eb}=p\varPsi_fi_b,i_b=\tfrac{\varPsi_f}{L_q-L_d}
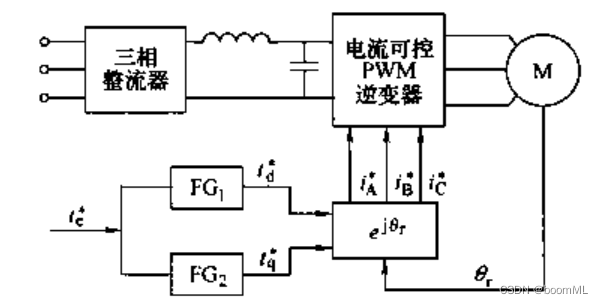
Teb=pΨfib,ib=Lq−LdΨf,根据最大转矩/电流比选择合适的定子电流
i
d
、
i
q
i_d、i_q
id、iq
控制简图
三、基于定子磁场定向的矢量控制
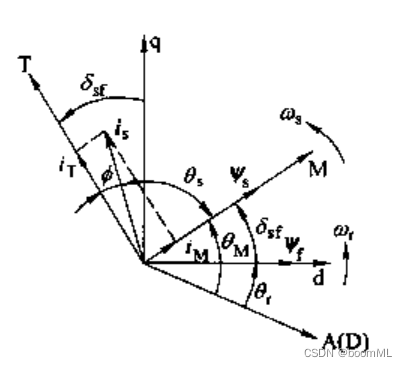
1.定子磁场定向
即为定子磁场与电驱磁场作用,以定子
Ψ
s
\varPsi_s
Ψs为参考设立M-T定子磁场同步旋转轴系
2.磁链方程与电压方程
{
Ψ
d
=
∣
Ψ
s
∣
cos
δ
s
f
Ψ
q
=
∣
Ψ
s
∣
sin
δ
s
f
,
{
Ψ
s
=
∣
Ψ
s
∣
e
j
θ
M
θ
M
=
δ
s
f
+
θ
r
\begin{cases}\varPsi_d=\mid\varPsi_s\mid\cos\delta_{sf}\\\varPsi_q=\mid\varPsi_s\mid\sin\delta_{sf}\end{cases},\begin{cases}\varPsi_s=\mid\varPsi_s\mid e^{j\theta_M}\\\theta_M=\delta_{sf}+\theta_r\end{cases}
{Ψd=∣Ψs∣cosδsfΨq=∣Ψs∣sinδsf,{Ψs=∣Ψs∣ejθMθM=δsf+θr
同理可得出电压方程为
{
u
M
=
R
S
i
M
+
d
Ψ
M
d
t
−
ω
s
Ψ
T
u
T
=
R
s
i
T
+
d
Ψ
T
d
t
+
ω
s
Ψ
M
\begin{cases}u_M=R_Si_M+\tfrac{d\varPsi_M}{dt}-\omega_s\varPsi_T\\u_T=Rsi_T+\tfrac{d\varPsi_T}{dt}+\omega_s\varPsi_M\end{cases}
{uM=RSiM+dtdΨM−ωsΨTuT=RsiT+dtdΨT+ωsΨM
由于定子磁场定向,则
Ψ
T
=
0
,
Ψ
M
=
Ψ
s
\varPsi_T=0,\varPsi_M=\varPsi_s
ΨT=0,ΨM=Ψs,则上式为
{
u
M
=
R
S
i
M
+
d
Ψ
M
d
t
u
T
=
R
s
i
T
+
ω
s
Ψ
M
\begin{cases}u_M=R_Si_M+\tfrac{d\varPsi_M}{dt}\\u_T=Rsi_T+\omega_s\varPsi_M\end{cases}
{uM=RSiM+dtdΨMuT=RsiT+ωsΨM
3.转矩方程
T e = p Ψ s × i s = p Ψ M i s sin θ s = p Ψ M i T T_e=p\varPsi_s\times i_s=p\varPsi_Mi_s\sin\theta_s=p\varPsi_Mi_T Te=pΨs×is=pΨMissinθs=pΨMiT
则由磁链方程电压方程和转矩方程可知, i M i_M iM为控制 Ψ s \varPsi_s Ψs的励磁分量, i T i_T iT为控制电磁转矩的转矩分量,上图中的 ϕ \phi ϕ为功率因素角,则可以通过控制 θ s \theta_s θs来控制 ϕ \phi ϕ。
 PMSM基于转子和定子磁场定向的矢量控制
PMSM基于转子和定子磁场定向的矢量控制




 本文详细介绍了基于转子和定子磁场定向的PMSM矢量控制,包括矢量控制基础、转子磁场定向的Clark和Park变换、磁链和电压方程,以及面装式和插入式PMSM的控制系统。通过对PMSM模型的坐标变换,实现了等效直流电机模型,便于转矩和弱磁的独立控制。
本文详细介绍了基于转子和定子磁场定向的PMSM矢量控制,包括矢量控制基础、转子磁场定向的Clark和Park变换、磁链和电压方程,以及面装式和插入式PMSM的控制系统。通过对PMSM模型的坐标变换,实现了等效直流电机模型,便于转矩和弱磁的独立控制。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








