本文深入探讨了同步磁阻电机的结构，包括轴向叠压、横向叠压和永磁辅助式PMASynRM。详细解释了其工作原理，强调了转子凸极性和磁阻转矩的作用。此外，文章还建立了不考虑磁路饱和与交叉饱和情况下的数学模型，包括A-B-C象限、α-β象限和d-q象限的磁链、电压和转矩方程，并对比分析了同步磁阻电机与开关磁阻电机的区别。
一、同步磁阻电机的结构
同步磁阻电机不含有转子磁场，只有电驱磁场起作用，所以又称为同步反应式电机。
1.轴向叠压
指的是沿着电机转动轴的垂直方向叠压磁障，结构复杂，制造成本高以及工艺加工要求高。
2.横向叠压
指的是沿着电机转动轴的方向叠压，也有分为外向叠压和内向叠压，横向叠片方式的转子结构结构简单，制造成本较低且容易，机械可靠性高。
3.永磁辅助式同步磁阻电机PMASynRM
在磁障中加入少量的永磁体，加入电磁转矩以增加转矩密度。
4.同步磁阻电机与开关磁阻电机的不同
在结构上是相同的，主要不同在控制器上，同步磁阻电机控制器采用交流变频器，开关磁阻电机控制器则是根据转子位置开通或关断相应的电流而产生磁场。
二、同步磁阻电机的工作原理（不考虑永磁辅助式）
1.转子的凸极特征
假如转子的结构为隐形式，此时
L
d
=
L
q
L_d=L_q
Ld=Lq，将不会产生磁阻转矩，同时也没有电磁转矩，则转子不会运动。
所以同步磁阻电机转子应为凸极结构，利用磁路的各向异性，根据磁路原则：磁通要沿着磁导最大（磁阻最小）的磁路闭合。
2.转子dq轴与磁阻转矩
d轴为无磁障处，q轴为磁障串联处，且q轴应滞后于d轴90°。
此时，d轴磁通路径走高导磁材料，磁阻较小，q轴磁通路径由导磁材料和非导磁材料串联而成，含有很多气隙，磁阻较大。且满足
L
d
>
L
q
，
L_d>L_q，
Ld>Lq，磁阻转矩为
T
e
=
p
(
L
d
−
L
q
)
∗
i
d
i
q
，
T_e=p(L_d-L_q)*i_di_q，
Te=p(Ld−Lq)∗idiq，所以此时凸极性强，产生较大的磁阻转矩。
三、同步磁阻电机的数学模型（不考虑磁路饱和与交叉饱和）
1.A-B-C象限
1.1磁链方程
[
Ψ
A
Ψ
B
Ψ
C
]
=
[
L
A
A
L
A
B
L
A
C
L
B
A
L
B
B
L
B
C
L
C
A
L
C
B
L
C
C
]
⋅
[
i
a
i
b
i
c
]
,
\begin{bmatrix}\Psi_A\\\Psi_B\\\Psi_C\end{bmatrix}=\begin{bmatrix}L_{AA} & L_{AB} & L_{AC}\\L_{BA}&L_{BB}&L_{BC}\\L_{CA}&L_{CB}&L_{CC}\end{bmatrix}\cdot\begin{bmatrix}i_a\\i_b\\i_c\end{bmatrix},
⎣
⎡ΨAΨBΨC⎦
⎤=⎣
⎡LAALBALCALABLBBLCBLACLBCLCC⎦
⎤⋅⎣
⎡iaibic⎦
⎤,
L
A
A
、
L
B
B
、
L
C
C
L_{AA}、L_{BB}、L_{CC}
LAA、LBB、LCC为自感，
{
L
A
A
=
L
σ
+
L
s
0
+
L
s
2
cos
2
θ
e
L
B
B
=
L
σ
+
L
s
0
+
L
s
2
cos
2
(
θ
e
−
12
0
∘
)
L
C
C
=
L
σ
+
L
s
0
+
L
s
2
cos
2
(
θ
e
+
12
0
∘
)
\begin{cases}L_{AA}=L_\sigma+L_{s0}+L_{s2}\cos2\theta_e\\L_{BB}=L_\sigma+L_{s0}+L_{s2}\cos2(\theta_e-120^\circ)\\L_{CC}=L_\sigma+L_{s0}+L_{s2}\cos2(\theta_e+120^\circ)\end{cases}
⎩
⎨
⎧LAA=Lσ+Ls0+Ls2cos2θeLBB=Lσ+Ls0+Ls2cos2(θe−120∘)LCC=Lσ+Ls0+Ls2cos2(θe+120∘)
L
A
B
、
L
B
A
、
L
B
C
、
L
C
B
、
L
C
A
L_{AB}、L_{BA}、L_{BC}、L_{CB}、L_{CA}
LAB、LBA、LBC、LCB、LCA为互感，
{
L
A
B
=
L
B
A
=
−
M
0
+
M
2
cos
2
(
θ
e
+
12
0
∘
)
L
B
C
=
L
C
B
=
−
M
0
+
M
2
cos
2
θ
e
L
C
A
=
L
A
C
=
−
M
0
+
M
2
cos
2
(
θ
e
−
12
0
∘
)
，
\begin{cases}L_{AB}=L_{BA}=-M_0+M_2\cos2(\theta_e+120^\circ)\\L_{BC}=L_{CB}=-M_0+M_2\cos2\theta_e\\L_{CA}=L_AC=-M_0+M_2\cos2(\theta_e-120^\circ)\end{cases}，
⎩
⎨
⎧LAB=LBA=−M0+M2cos2(θe+120∘)LBC=LCB=−M0+M2cos2θeLCA=LAC=−M0+M2cos2(θe−120∘)，
其中
L
σ
L_\sigma
Lσ为漏感，
L
s
0
L_{s0}
Ls0为自感基波，
L
s
2
L_{s2}
Ls2为自感二次谐波幅值，
M
0
M_0
M0为互感基波，
M
2
M_2
M2为互感二次谐波幅值。
1.2电压方程
[ U a U b U c ] = [ R s 0 0 0 R s 0 0 0 R s ] ⋅ [ i a i b i c ] + p [ Ψ a Ψ b Ψ c ] \begin{bmatrix}U_a\\U_b\\U_c\end{bmatrix}=\begin{bmatrix}R_s&0&0\\0&R_s&0\\0&0&R_s\end{bmatrix}\cdot\begin{bmatrix}i_a\\i_b\\i_c\end{bmatrix}+p\begin{bmatrix}\Psi_a\\\Psi_b\\\Psi_c\end{bmatrix} ⎣ ⎡UaUbUc⎦ ⎤=⎣ ⎡Rs000Rs000Rs⎦ ⎤⋅⎣ ⎡iaibic⎦ ⎤+p⎣ ⎡ΨaΨbΨc⎦ ⎤
1.3方程中依然有 θ e \theta_e θe的存在
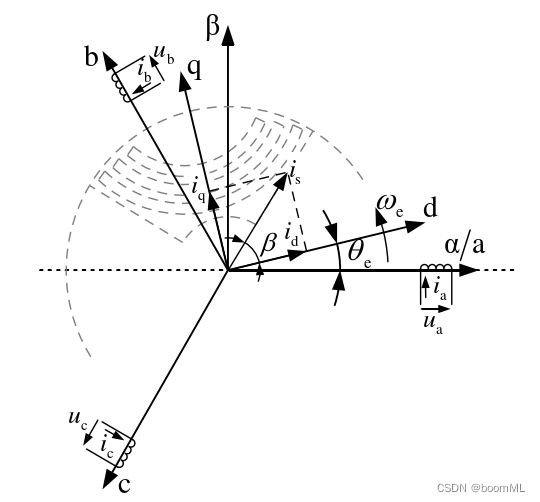
2. α − β \alpha-\beta α−β象限
经过Clark坐标变换可以将A-B-C三相静止坐标系转换到两相静止坐标系
3. d − q d-q d−q象限
经过Park坐标变换可以将两相静止坐标系转换到两相旋转同步坐标系
3.1磁链方程
[ Ψ d Ψ q ] = [ L d 0 0 L q ] ⋅ [ i d i q ] \begin{bmatrix}\Psi_d\\\Psi_q\end{bmatrix}=\begin{bmatrix}L_d&0\\0&L_q\end{bmatrix}\cdot\begin{bmatrix}i_d\\i_q\end{bmatrix} [ΨdΨq]=[Ld00Lq]⋅[idiq]
3.2电压方程
[ U d U q ] = [ R s 0 0 R s ] ⋅ [ i d i q ] + [ p − ω e ω e p ] ⋅ [ Ψ d Ψ q ] ， ω e = 2 π f \begin{bmatrix}U_d\\U_q\end{bmatrix}=\begin{bmatrix}R_s&0\\0&R_s\end{bmatrix}\cdot\begin{bmatrix}i_d\\i_q\end{bmatrix}+\begin{bmatrix}p&-\omega_e\\\omega_e&p\end{bmatrix}\cdot\begin{bmatrix}\Psi_d\\\Psi_q\end{bmatrix}，\omega_e=2\pi f [UdUq]=[Rs00Rs]⋅[idiq]+[pωe−ωep]⋅[ΨdΨq]，ωe=2πf为电机电角度。
3.3转矩方程
T e = C ⋅ p ( L d − L q ) i d i q ， T_e=C\cdot p(L_d-L_q)i_di_q， Te=C⋅p(Ld−Lq)idiq，该转矩为磁阻转矩，当为恒功率状态下， C = 3 2 ， C=\frac{\sqrt{3}}{2}， C=23，当为恒幅值状态下 C = 3 2 。 C=\frac{3}{2}。 C=23。
3.4此时实现完全解耦
四、永磁辅助式磁阻电机的数学模型（不考虑磁路饱和与交叉饱和）
4.1磁链方程
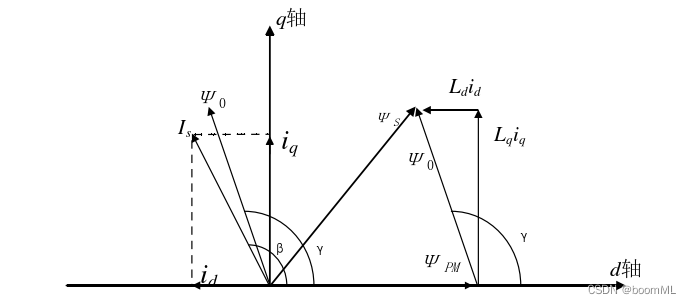
[ Ψ d Ψ q ] = [ L d 0 0 L q ] ⋅ [ i d i q ] + [ Ψ p m 0 ] \begin{bmatrix}\Psi_d\\\Psi_q\end{bmatrix}=\begin{bmatrix}L_d&0\\0&L_q\end{bmatrix}\cdot\begin{bmatrix}i_d\\i_q\end{bmatrix}+\begin{bmatrix}\Psi_{pm}\\0\end{bmatrix} [ΨdΨq]=[Ld00Lq]⋅[idiq]+[Ψpm0]
4.2电压方程
[ U d U q ] = [ R s 0 0 R s ] ⋅ [ i d i q ] + [ p − ω e ω e p ] ⋅ [ Ψ d Ψ q ] ， ω e = 2 π f \begin{bmatrix}U_d\\U_q\end{bmatrix}=\begin{bmatrix}R_s&0\\0&R_s\end{bmatrix}\cdot\begin{bmatrix}i_d\\i_q\end{bmatrix}+\begin{bmatrix}p&-\omega_e\\\omega_e&p\end{bmatrix}\cdot\begin{bmatrix}\Psi_d\\\Psi_q\end{bmatrix}，\omega_e=2\pi f [UdUq]=[Rs00Rs]⋅[idiq]+[pωe−ωep]⋅[ΨdΨq]，ωe=2πf为电机电角度。
4.3转矩方程
T e = C ⋅ p ( Ψ p m i q + ( L d − L q ) i d i q ) ， T_e=C\cdot p(\Psi_{pm}i_q+(L_d-L_q)i_di_q)， Te=C⋅p(Ψpmiq+(Ld−Lq)idiq)，前面一项为电磁转矩，后面一项为磁阻转矩，磁阻转矩大小由 L d − L q L_d-L_q Ld−Lq确定，当为恒功率状态下， C = 3 2 ， C=\frac{\sqrt{3}}{2}， C=23，当为恒幅值状态下 C = 3 2 。 C=\frac{3}{2}。 C=23。
4.4矢量图
五、同步磁阻电机磁路饱和与交叉饱和
1.磁路饱和
2.交叉饱和
{ L d = L d ( i d ， i q ) L q = L q ( i d ， i q ) \begin{cases}L_d=L_d(i_d，i_q)\\L_q=L_q(i_d，i_q)\end{cases} {Ld=Ld(id，iq)Lq=Lq(id，iq)
扫一扫
9万+
到【灌水乐园】发言
